Pole powierzchni trójkąta

Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom rozszerzony

pole powierzchni trójkąta
wzory ma pole trójkąta:
- P=\frac{1}{2}\cdot a\cdot b
- P=\frac{1}{2}\cdot a\cdot b\cdot \sin\alpha
wzór Herona P=\sqrt{p(p-a)(p-b)(p-c)}
promień okręgu wpisanego w trójkąt prostokątny

Zadanie 1. (2 pkt)

[ ⇒ Dodaj do testu ] Numer zadania: pr-20748

Podpunkt 1.1 (2 pkt)

Dane są pola powierzchni trzech trójkątów na rysunku:

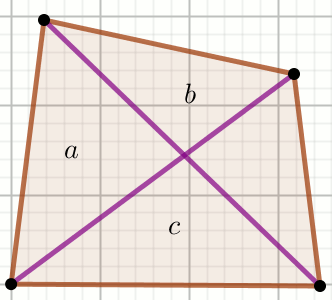
Oblicz pole powierzchni czwartego z trójkataów.

Dane

a=11
b=9
c=5

Odpowiedź:

Wpisz odpowiedź: (liczba zapisana dziesiętnie)

Zadanie 2. (2 pkt)

[ ⇒ Dodaj do testu ] Numer zadania: pr-20567

Podpunkt 2.1 (2 pkt)

Dany jest trójkąt ABC:

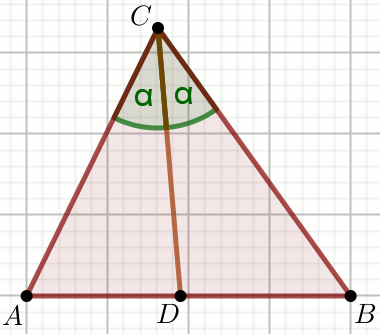
Oblicz pole powierzchni tego trójkąta.

Dane

|AC|=6
|BC|=12
P_{\triangle DBC}-P_{\triangle ADC}=6\sqrt{3}=10.39230484541326

Odpowiedź:

Wpisz odpowiedź: (liczba zapisana dziesiętnie)

Zadanie 3. (4 pkt)

[ ⇒ Dodaj do testu ] Numer zadania: pr-30381

Podpunkt 3.1 (4 pkt)

« W trójkąt prostokątny wpisano okrąg o promieniu r. Tangens kąta ostrego tego trójkąta jest równy 0,75.

Oblicz odległość wierzchołka kąta prostego trójkąta od punktu styczności tego okręgu z przeciwprostokątną trójkąta.

Dane

r=100

Odpowiedź:

Wpisz odpowiedź: (liczba zapisana dziesiętnie)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm

Matury CKE ☆ Sprawdziany ☆ Zadania ☆ Zbiór zadań ☆ Rankingi ☆ Pomoc	Zaloguj mnie... Załóż konto...