Pola trójkątów podobnych
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom podstawowy
|
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10587 |
Podpunkt 1.1 (1 pkt)
Trójkąty ABC i
A'B'C' są podobne, a ich pola powierzchni są odpowiednio,
równe 10 cm2 i
12 cm2. Wyznacz skalę podobieństwa
\frac{|A'B'|}{|AB|} i zapisz wynik
w najprostszej postaci
\frac{a\sqrt{b}}{c}, gdzie
a,b,c\in\mathbb{N}.
Podaj liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10586 |
Podpunkt 2.1 (1 pkt)
« Najkrótsze wysokości dwóch trójkątów podobnych pozostają w stosunku
5:17. Pola tych trójkątów mogą być równe:
Odpowiedzi:
| A. 2 i \frac{289}{5} | B. 2 i \frac{34}{5} |
| C. 1 i \frac{34}{5} | D. 10 i \frac{578}{5} |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10591 |
Podpunkt 3.1 (1 pkt)
Trójkąt ABC jest podobny do trójkąta
A_1B_1C_1 w skali
k=\frac{14}{11}.
Oblicz stosunek pola powierzchni trójkąta ABC do pola powierzchni trójkąta A_1B_1C_1.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10515 |
Podpunkt 4.1 (1 pkt)
« Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku
49:121, mogą być równe:
Odpowiedzi:
| A. 33:14 | B. 11:\frac{49}{11} |
| C. 7:\frac{49}{11} | D. 14:\frac{147}{11} |
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20760 |
Podpunkt 5.1 (2 pkt)
» Trójkąt ABC jest ostrokątny i równoramienny o
podstawie AB:
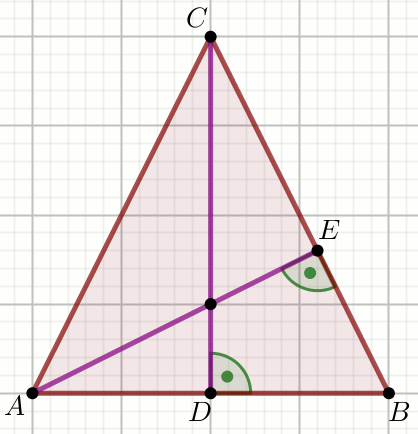

Oblicz P_{ABC}.
Dane
|AB|+|BC|+|AC|=480
\frac{P_{\triangle ABE}}{P_{\triangle ADC}}=\frac{36}{25}=1.44000000000000
\frac{P_{\triangle ABE}}{P_{\triangle ADC}}=\frac{36}{25}=1.44000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20774 |
Podpunkt 6.1 (1 pkt)
« Odcinki DE,
FG i AB
są równoległe, a pola wielokątów DEC,
FGED i ABGF
pozostają w stosunku a:b:c.
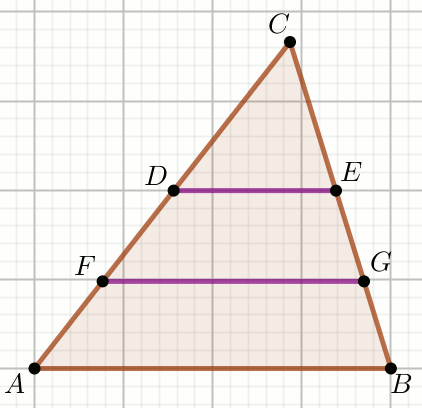

Oblicz \frac{|DE|}{|FG|}.
Dane
a=9
b=27
c=13
b=27
c=13
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Oblicz \frac{|FG|}{|AB|}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20756 |
Podpunkt 7.1 (2 pkt)
« Dane są punkty na okręgu:
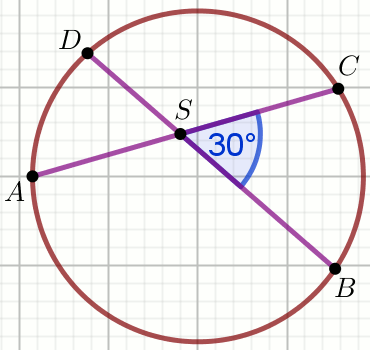

Oblicz P_{\triangle ASD}.
Dane
|AS|=17
|SB|=18
|SC|=5
|SB|=18
|SC|=5
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20757 |
Podpunkt 8.1 (1 pkt)
» Dany jest trójkąt równoramienny o podstawie
AB:
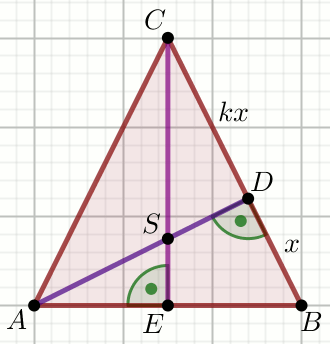

Oblicz \sin\sphericalangle DAB.
Dane
k=6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Oblicz
\frac{P_{\triangle AES}}{P_{\triangle SDC}}
.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20758 |
Podpunkt 9.1 (2 pkt)
Dany jest trójkąt:
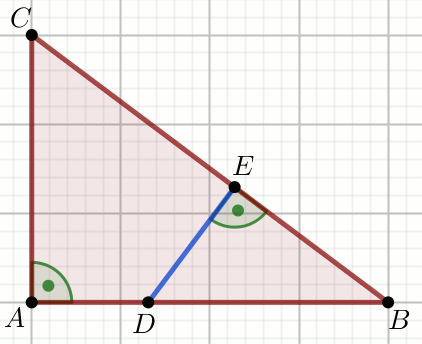

Oblicz |DE|.
Dane
|AC|=24
P_{\triangle DBE}:P_{ADEC}=266:574=0.46341463414634
P_{\triangle DBE}:P_{ADEC}=266:574=0.46341463414634
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20759 |
Podpunkt 10.1 (2 pkt)
Trójkąt ABC jest równoramienny o podstawie
AB, a odcinek DE jest
równoległy do podstawy AB:
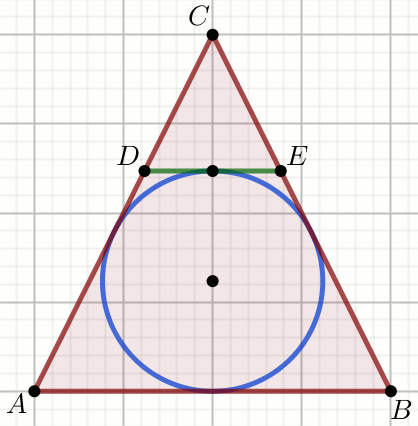

Oblicz P_{DEC}.
Dane
|AC|=|BC|=74
|AB|=48
|AB|=48
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)