Przesunięcię równoległe wykresu funkcji
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom podstawowy
|
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10778 |
Podpunkt 1.1 (1 pkt)
« Dany jest wykres funkcji y=f(x).
Aby otrzymać wykres funkcji g(x)=f(x+4)+3 wykres funkcji f należy przesunąć o wektor o współrzędnych \vec{u}=[p, q].
Podaj współrzędne p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11570 |
Podpunkt 2.1 (1 pkt)
Wykres funkcji g(x)=(x+4)^4+4
można otrzymać przesuwając wykres funkcji f(x)=x^4
o wektor \vec{u}=[p,q].
Podaj współrzędne wektora p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10787 |
Podpunkt 3.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
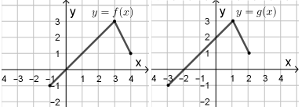
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x)+2 | B. g(x)=f(x)-2 |
| C. g(x)=f(x+2) | D. g(x)=f(x-1) |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10788 |
Podpunkt 4.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
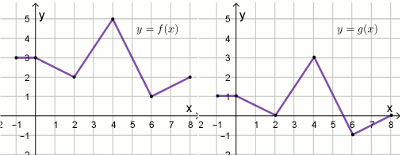
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x)-2 | B. g(x)=f(x-2) |
| C. g(x)=f(x)+2 | D. g(x)=f(x+2) |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10789 |
Podpunkt 5.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
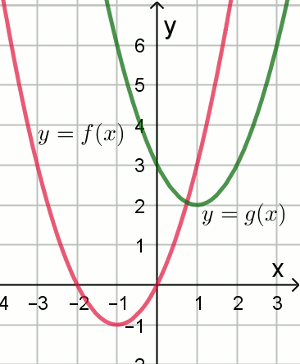
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x+2)+3 | B. g(x)=f(x-2)+3 |
| C. g(x)=f(x-2)-3 | D. g(x)=f(x+3)-2 |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10769 |
Podpunkt 6.1 (1 pkt)
« Na rysunku przedstawiony jest wykres funkcji
y=f(x).
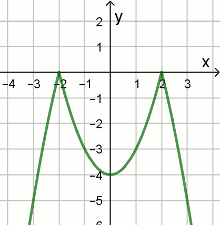

Które z równań ma dokładnie trzy rozwiązania:
Odpowiedzi:
| A. f(x-1)=4 | B. f(x-4)=-1 |
| C. f(x+2)=-1 | D. f(x+2)+4=0 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10770 |
Podpunkt 7.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
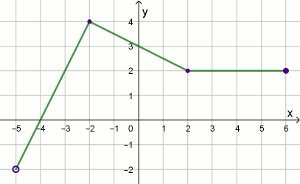

Zbiorem wartości funkcji g, gdzie g(x)=f(x)-3, jest zbiór:
Odpowiedzi:
| A. (-2,9\rangle | B. (1,7\rangle |
| C. (-8,3\rangle | D. (-5,1\rangle |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10772 |
Podpunkt 8.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
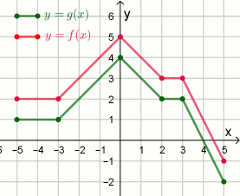
Funkcja f określona jest wzorem:

Odpowiedzi:
| A. f(x)=g(x)+1 | B. f(x)=g(x)-1 |
| C. f(x)=g(x+1) | D. f(x)=g(x-1) |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10773 |
Podpunkt 9.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
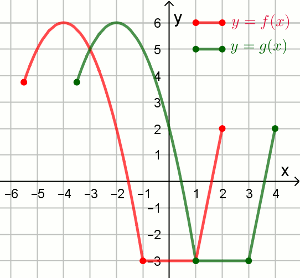
Funkcja f określona jest wzorem:

Odpowiedzi:
| A. f(x)=g(x+2) | B. f(x)=g(x-2) |
| C. f(x)=g(x)-2 | D. f(x)=g(x)+2 |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10774 |
Podpunkt 10.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
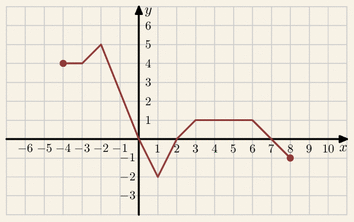
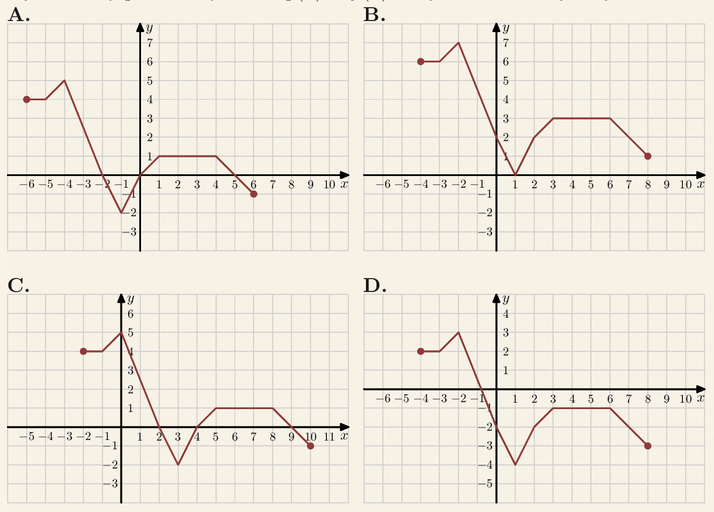

Na którym rysunku przedstawiony jest wykres funkcji y=f(x+2):

Odpowiedzi:
| A. C | B. A |
| C. B | D. D |
| Zadanie 11. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10775 |
Podpunkt 11.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
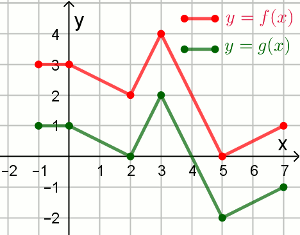
Funkcja f określona jest wzorem:

Odpowiedzi:
| A. f(x)=g(x)+2 | B. f(x)=g(x)-2 |
| C. f(x)=g(x-2) | D. f(x)=g(x+2) |
| Zadanie 12. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10777 |
Podpunkt 12.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
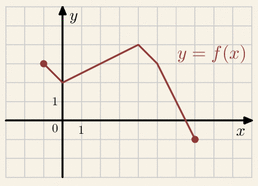
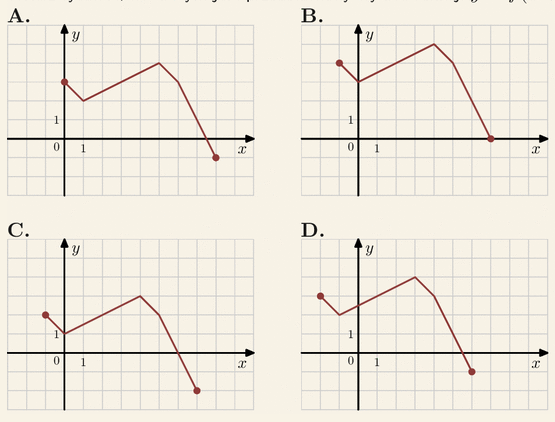

Na którym rysunku przedstawiony jest wykres funkcji y=f(x+1):

Odpowiedzi:
| A. C | B. A |
| C. D | D. B |
| Zadanie 13. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10765 |
Podpunkt 13.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
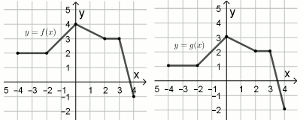
Funkcja f określona jest wzorem:

Odpowiedzi:
| A. f(x)=g(x-1)+1 | B. f(x)=g(x)+1 |
| C. f(x)=g(x)-1 | D. f(x)=g(x-1) |
| E. f(x)=g(x+1) | F. f(x)=g(x-1)-1 |
| Zadanie 14. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11570 |
Podpunkt 14.1 (1 pkt)
Wykres funkcji g(x)=(x+4)^4+4
można otrzymać przesuwając wykres funkcji f(x)=x^4
o wektor \vec{u}=[p,q].
Podaj współrzędne wektora p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 15. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11571 |
Podpunkt 15.1 (1 pkt)
Wykres funkcji f(x)=x^2+2x+2 przesunięto
o wektor \vec{u}=[7,-6] i otrzymano wykres funkcji
określonej wzorem g(x)=x^2+bx+c.
Podaj liczby b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 16. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20290 |
Podpunkt 16.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji f,
który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem
y=\frac{1}{x} dla każdej liczby rzeczywistej
x\neq 0.
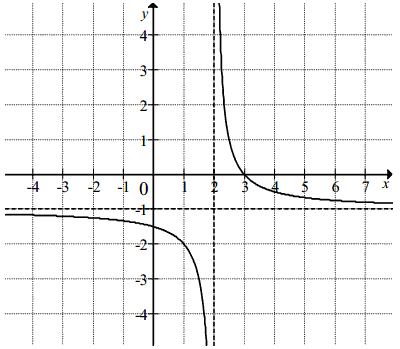

Odczytaj zbiór tych argumentów, dla których funkcja przyjmuje wartości dodatnie. Podaj liczbę występującą w środku tego zbioru.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (1 pkt)
Podaj miejsce zerowe funkcji g określonej wzorem
g(x)=f(x-4).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20781 |
Podpunkt 17.1 (1 pkt)
» Dane są funkcje f oraz
g, przy czym
g(x)=f(x+5)-10.
Oblicz g(-2).
Dane
f(3)=-9
f(-2)=5
y_0=-5
f(-2)=5
y_0=-5
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.2 (1 pkt)
Podaj wartość argumentu, dla którego funkcja g
przyjmuje wartość y_0.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 18. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20296 |
Podpunkt 18.1 (1 pkt)
» Dana jest funkcja f(x)=\frac{2093}{x}, gdzie
x\neq 0. Jej wykres przesunięto wzdłuż osi
Oy i otrzymano wykres funkcji
y=g(x), do którego należy punkt
B=(23,108). Wyznacz wektor tego przesunięcia
\vec{u}=[u_x,u_y].
Podaj u_y.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.2 (1 pkt)
Ile liczb naturalnych k ze zbioru
\{0,1,2,3,...,173\} ma tę własność, że liczba
g(k) jest całkowita?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)