Podział czworokątów - romby i równoległoboki
Zadania dla klasy drugiej liceum ogólnokształcącego - poziom rozszerzony
- czworokąty
- romby
- równoległoboki
- planimetria
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20115 |
Podpunkt 1.1 (2 pkt)
» Czworokąt na rysunku jest prostokątem:
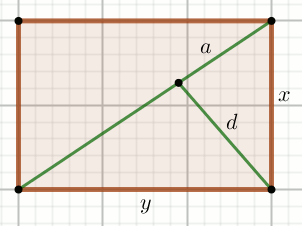

Oblicz a.
Dane
x=27
y=36
d=28
y=36
d=28
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20118 |
Podpunkt 2.1 (2 pkt)
Krótsza przekątna równoległoboku ma długość a, zaś
dłuższa przekątna długość b. Przekątne te przecinają
się pod takim kątem \alpha, że
\cos\alpha=0,25.
Oblicz obwód tego równoległoboku.
Dane
a=7
b=14
b=14
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20119 |
Podpunkt 3.1 (2 pkt)
» Czworokąt na rysunku jest rombem:
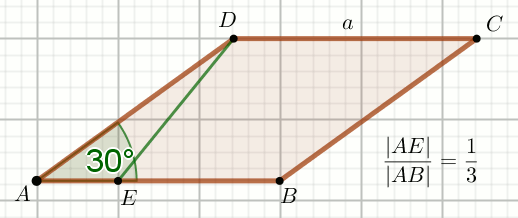

Oblicz |DE|.
Dane
a=39
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20120 |
Podpunkt 4.1 (2 pkt)
» Boki równoległoboku mają długość |AB|=7
i |BC|=6, a jego krótsza przekątna długość
|BD|=8:
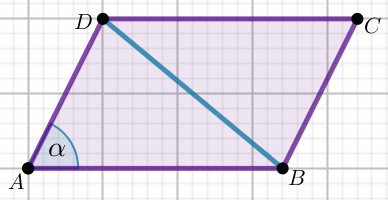

Oblicz \sin\alpha.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20121 |
Podpunkt 5.1 (2 pkt)
Boki równoległoboku mają długość |AB|=22
i |BC|=11\sqrt{3}, a kąt
\alpha miarę
150^{\circ}:
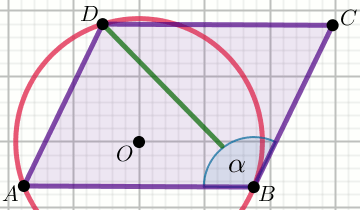

Oblicz obwód okręgu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20122 |
Podpunkt 6.1 (2 pkt)
W równoległoboku ABCD punkty E i
F są środkami boków, a odcinek EF
ma długość 26\sqrt{3}:
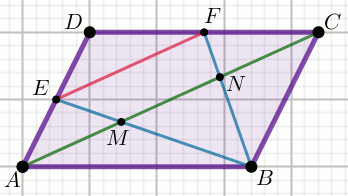

Oblicz |MN|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20123 |
Podpunkt 7.1 (2 pkt)
W równoległoboku ABCD dane sa długości odcinków
|OE|=\frac{13}{2} i |OF|=\frac{91}{8},
oraz miara kąta \alpha=30^{\circ}:
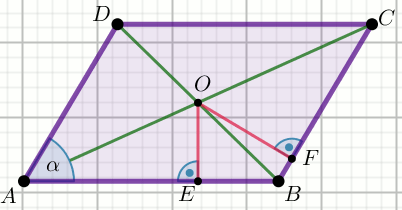

Oblicz |BD|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20124 |
Podpunkt 8.1 (2 pkt)
W czworokącie ABCD o obwodzie długości L=104
i przekątnej |BD|=26, kąt rozwarty ma miarę \alpha=120^{\circ}:
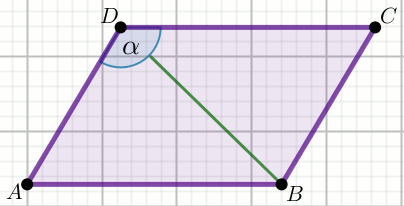

Oblicz długość dłuższego boku tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20125 |
Podpunkt 9.1 (1 pkt)
« W równoległoboku |AB|=20 i
|AE|=|DE|=4:
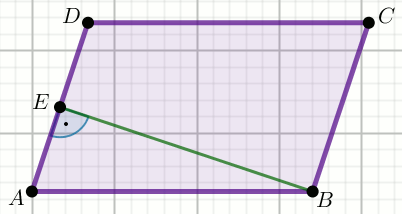

Oblicz długość krótszej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20116 |
Podpunkt 10.1 (2 pkt)
» Dłuższa przekątna rombu o boku długości a ma
długość d.
Oblicz cosinus kąta ostrego tego rombu.
Dane
a=\frac{7}{2}=3.50000000000000
d=5=5.00000000000000
d=5=5.00000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20117 |
Podpunkt 11.1 (1 pkt)
W prostokącie ABCD odcinki
AE, EF i FC
mają równą długość równą 27\sqrt{2}:
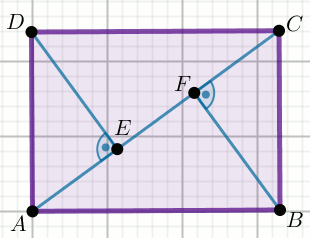

Jaką długość ma jego krótszy bok?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Jaką długość ma jego dłuższy bok?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30095 |
Podpunkt 12.1 (2 pkt)
« Czworokąt na rysunku jest kwadratem:
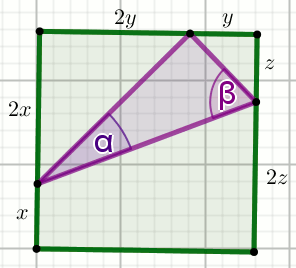

Uzasadnij, że fioletowy trójkąt jest prostokątny.
Oblicz \tan\alpha.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (2 pkt)
Oblicz \tan\beta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30096 |
Podpunkt 13.1 (2 pkt)
« Czworokąt na rysunku jest prostokątem
(x \lessdot y):
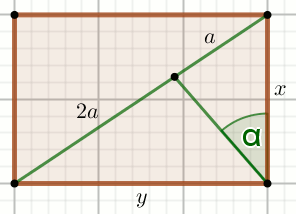

Oblicz \sin\alpha.
Dane
x=27
y=36
y=36
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30097 |
Podpunkt 14.1 (4 pkt)
« Czworokąt na rysunku jest prostokątem, w którym
|ES|=12, |AF|=30
i |BC|=24:
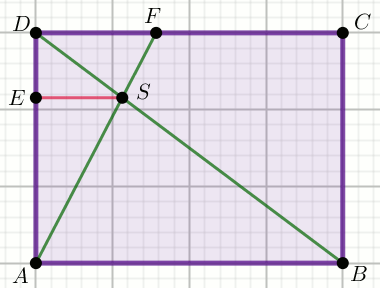

Oblicz długość dłuższego boku tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30098 |
Podpunkt 15.1 (2 pkt)
Czworokąt ABCD na rysunku jest prostokątem, w którym
|BC|=16, |CE|=12,
|DE|=8 i |BF|=6:
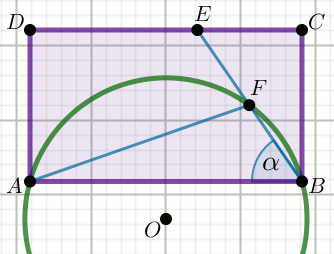

Oblicz \sin\alpha.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.2 (2 pkt)
Na trójkącie ABF opisano okrąg o środku w punkcie
O.
Oblicz długość promienia tego okręgu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30099 |
Podpunkt 16.1 (4 pkt)
» Czworokąt na rysunku jest prostokątem:
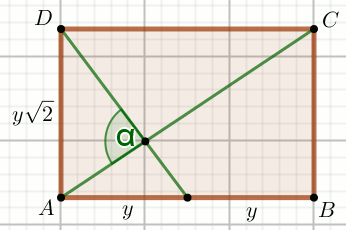

Oblicz \cos\alpha.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30100 |
Podpunkt 17.1 (4 pkt)
Czworokąt ABCD na rysunku jest równoległobokiem, w którym
|BC|=10:
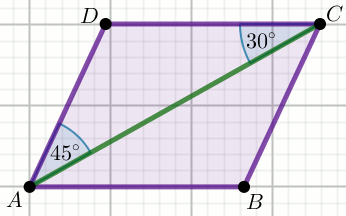

Oblicz |AC|^2+|BD|^2.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)