Podział czworokątów - czworokąty i wielokąty
Zadania dla klasy drugiej liceum ogólnokształcącego - poziom podstawowy
- czworokąty
- wielokąty
- planimetria
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11089 |
Podpunkt 1.1 (1 pkt)
Oceń, które z poniższych zdań są prawdziwe:
Odpowiedzi:
| T/N : w każdy prostokąt można wpisać okrąg | T/N : w każdy romb można wpisać okrąg |
| T/N : w każdy czworokąt można wpisać okrąg |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11477 |
Podpunkt 2.1 (1 pkt)
Dłuższa przekątna sześciokąta foremnego ma długość 4\sqrt{6}.
Oblicz pole powierzchni tego sześciokąta i zapisz wynik w najprostszej postaci
\frac{a\sqrt{b}}{c}, gdzie a,b,c\in\mathbb{N}
Podaj liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11473 |
Podpunkt 3.1 (1 pkt)
Wielokąt foremny ma n=19 kątów. Jeden kąt wewnętrzny tego wielokąta ma miarę stopniową
\frac{\{.........\}}{19}^{\circ}.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11476 |
Podpunkt 4.1 (1 pkt)
Wielokąt wypukły ma n=9 kątów, a liczba jego
przekątnych jest równa \{.........\}.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11478 |
Podpunkt 5.1 (1 pkt)
Wielokąt wypukły ma n=65 przekątnych, a liczba jego
kątów jest równa \{.........\}.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11479 |
Podpunkt 6.1 (1 pkt)
Suma miar wszystkich kątów wewnętrznych wielokąta wypukłego jest
równa 2520^{\circ}. Wynika z tego, że wielokąt ten
na \{.........\} kątów wewnętrznych.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11484 |
Podpunkt 7.1 (1 pkt)
« Z kwadratu o boku długości 3 odcięto cztery naroża
(cztery trójkąty równoramienne) i otrzymano ośmiokąt foremny.
Bok tego ośmiokąta ma długość a+b\sqrt{2}, gdzie
a,b\in\mathbb{Z}.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11483 |
Podpunkt 8.1 (1 pkt)
Kwadrat K_1 jest obrazem kwadratu
K w podobieństwie o skali
\frac{5}{6}. Przekątna kwadratu
K_1 ma długość \frac{10}{3}.
Wówczas bok kwadratu K ma długość a\sqrt{2}.
Podaj liczbę a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20452 |
Podpunkt 9.1 (2 pkt)
» Liczba boków wielokąta i liczba jego przekątnych dają w sumie
p.
Ile boków ma ten wielokąt?
Dane
p=153
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20453 |
Podpunkt 10.1 (2 pkt)
» BD jest przekątną czworokąta wypukłego
ABCD o obwodzie p, w którym
|AB|+|BD|+|AD|=m i
|BC|+|CD|+|BD|=n.
Oblicz długość przekątnej BD.
Dane
p=50
m=38
n=42
m=38
n=42
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20454 |
Podpunkt 11.1 (1 pkt)
Czworokąt wpisany jest w okrąg, a kąty \alpha
i \beta mają miary:
\alpha=12^{\circ} i \beta=28^{\circ}:
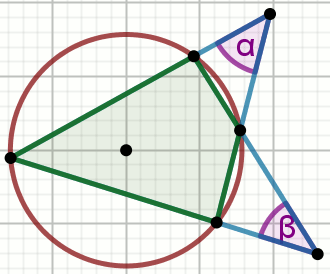

Wyznacz miarę najmniejszego kąta tego czworokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Wyznacz miarę największego kąta tego czworokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)