Czworokąty - okrąg wpisany w czworokąt
Zadania dla klasy drugiej liceum ogólnokształcącego - poziom rozszerzony
- czworokąty
- okrąg wpisany na czworokącie
- warunek wpisaniu okręgu w czworokąt
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20135 |
Podpunkt 1.1 (1 pkt)
» Czworokąt na rysunku jest trapezem równoramiennym:
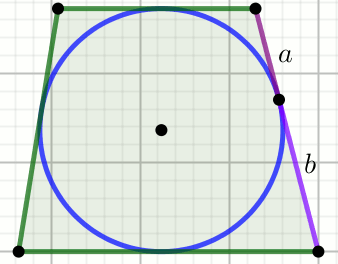

Oblicz długość promienia niebieskiego okręgu.
Dane
a=5
b=45
b=45
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 1.2 (1 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20136 |
Podpunkt 2.1 (2 pkt)
» Czworokąt na rysunku jest trapezem:
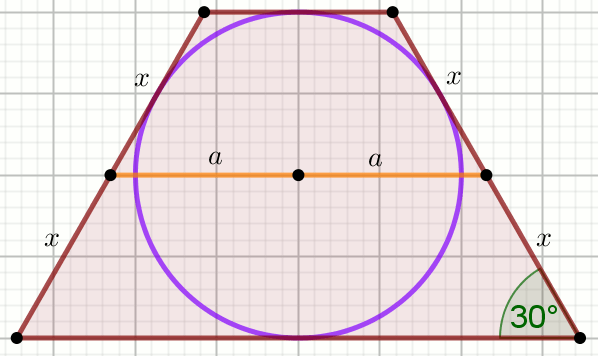

Oblicz długość promienia okręgu.
Dane
a=7
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20137 |
Podpunkt 3.1 (1 pkt)
Czworokąt na rysunku jest trapezem równoramiennym:
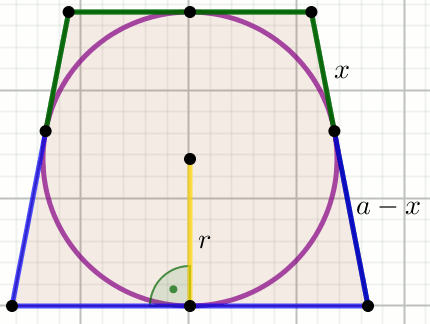

Oblicz długość zielonej łamanej.
Dane
a=50
r=20
r=20
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (1 pkt)
Oblicz długość niebieskiej łamanej.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20138 |
Podpunkt 4.1 (2 pkt)
Czworokąt na rysunku jest trapezem, a czerwony odcinek ma długość
a:
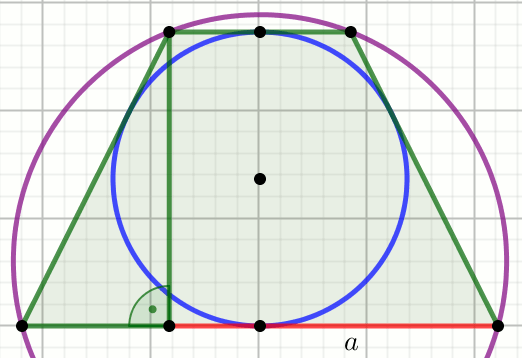

Oblicz obwód tego trapezu.
Dane
a=9
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20139 |
Podpunkt 5.1 (1 pkt)
W trapez o obwodzie długości 54 i stosunku
ramion równym \frac{10}{17}, wpisano okrąg o promieniu długości
4.
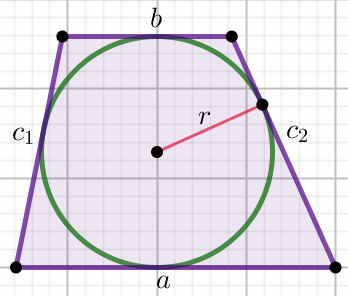

Podaj długość krótszej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (1 pkt)
Podaj długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20140 |
Podpunkt 6.1 (2 pkt)
« W trapez ABCD wpisano okrąg taki, że
|AE|=16, |BE|=8 i
|OE|=4:
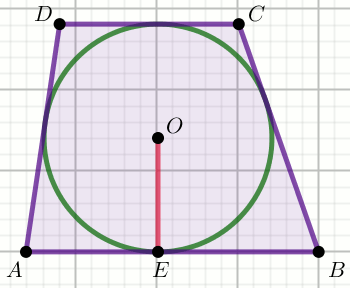
Wyznacz długość obwodu tego trapezu.

Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20141 |
Podpunkt 7.1 (1 pkt)
Przedstawiony na rysunku trapez jest równoramienny ma obwód o długości
104, w którym przekątna AC
ma długość2\sqrt{313}:
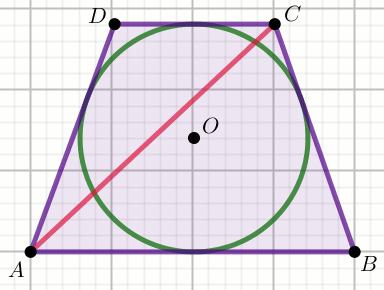

Wyznacz długość najkrótszego boku tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.2 (1 pkt)
Wyznacz długość najdłuższego boku tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20142 |
Podpunkt 8.1 (2 pkt)
» W trapez ABCD wpisano okrąg taki, że
|AE|=32, |BE|=36 i
|OE|=24:

Oblicz długość krótszej podstawy tego trapezu.

Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30103 |
Podpunkt 9.1 (4 pkt)
» Czworokąt na rysunku jest trapezem prostokątnym:
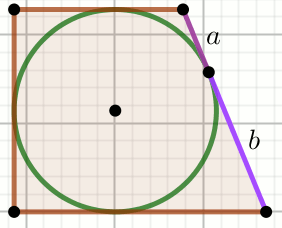

Oblicz obwód tego trapezu.
Dane
a=5
b=20
b=20
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30105 |
Podpunkt 10.1 (1 pkt)
» Czworokąt na rysunku jest rombem:
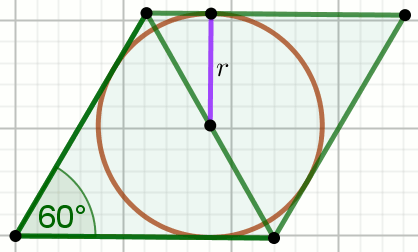

Oblicz długość krótszej przekątnej tego rombu.
Dane
r=8\sqrt{3}=13.8564064605510180
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego rombu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.3 (1 pkt)
Oblicz długość krótszego z odcinków, na które punkt styczności podzielił
bok tego rombu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.4 (1 pkt)
Oblicz długość dłuższego z odcinków, na które punkt styczności podzielił
bok tego rombu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30106 |
Podpunkt 11.1 (2 pkt)
Obwód trapezu pokazanego na rysunku ma długość 140,
a jego przekątna AC długość 37:
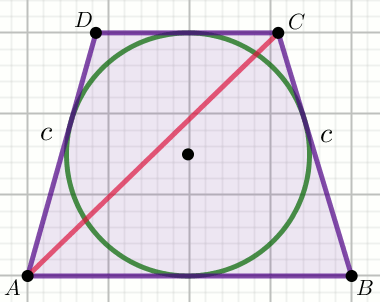

Oblicz długość promienia okręgu wpisanego w ten trapez.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (2 pkt)
Oblicz długość promienia okręgu opisanego na tym trapezie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30107 |
Podpunkt 12.1 (2 pkt)
Czworokąt na rysunku jest trapezem równoramiennym o podstawie
AB, w którym przekątna AC
ma długość 2\sqrt{313}, a ramię BC
długość 26:
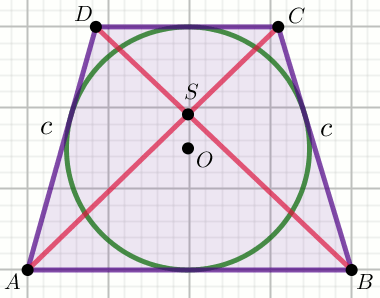

Wyznacz odległość punktu S od dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (2 pkt)
Oblicz odległość punktu S od ramienia tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30108 |
Podpunkt 13.1 (2 pkt)
« Na okręgu opisano trapez równoramienny ABCD.
Przekątna AC tego trapezu ma długość
4\sqrt{514}, a jego obwód długość
272:


Oblicz długość krótszej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (2 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30109 |
Podpunkt 14.1 (2 pkt)
» Czworokąt na rysunku jest trapezem równoramiennym, w którym
|OE|=18 oraz
|CE|=x i |BE|=4x:
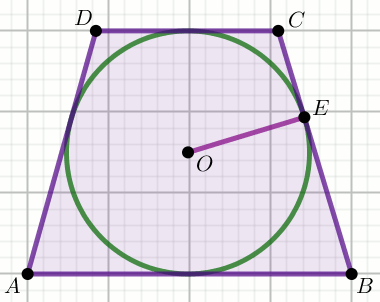

Oblicz x.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (2 pkt)
Oblicz \cos \alpha, gdzie
\alpha jest kątem przy podstawie pomiędzy przekątną
trapezu a ramieniem tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30110 |
Podpunkt 15.1 (2 pkt)
«« Czworokąt na rysunku jest trapezem równoramiennym, w którym
r=\frac{3\sqrt{5}}{5}}:
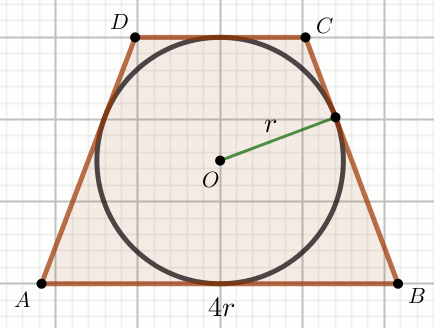

Oblicz |AO|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.2 (2 pkt)
Oblicz |DO|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30104 |
Podpunkt 16.1 (2 pkt)
W trapez równoramienny ABCD, w którym odcinek
CD jest krótszą podstawą, wpisano okrąg o promieniu
długości r=8\sqrt{3}. Punkt
K jest punktem wspólnym okręgu i ramienia
AD i jest tak położony, że
|AK|:|KD|=3.
Podaj |AD|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (2 pkt)
Podaj \cos \sphericalangle ABD.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30112 |
Podpunkt 17.1 (2 pkt)
» Przekątna w trapezie równoramiennym ma długość
3\sqrt{514}. Obwód tego trapezu ma długość
204, a suma jego podstaw jest równa 102.
Podaj długość najkrótszego boku tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.2 (2 pkt)
Podaj długość najdłuższego boku tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)