Pole powierzchni rombu i równoległoboku
Zadania dla klasy drugiej liceum ogólnokształcącego - poziom rozszerzony
- pole powierzchni rombu
- pole powierzchni równoległoboku
- wzory na pole rombu i równoległoboku
- własności pola powierzchni
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20147 |
Podpunkt 1.1 (1 pkt)
» Czworokąt na rysunku jest rombem:
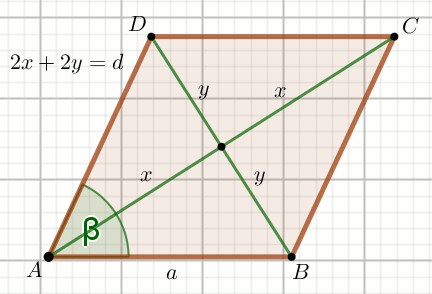

Oblicz jego pole powierzchni.
Dane
a=13
d=34
d=34
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 1.2 (1 pkt)
Oblicz \sin\beta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20148 |
Podpunkt 2.1 (2 pkt)
» Czworokąt na rysunku jest równoległobokiem:
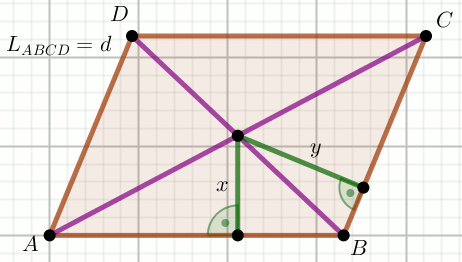

Oblicz jego pole powierzchni.
Dane
x=6
y=8
d=70
y=8
d=70
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20149 |
Podpunkt 3.1 (2 pkt)
« Czworokąt na rysunku jest równoległobokiem:
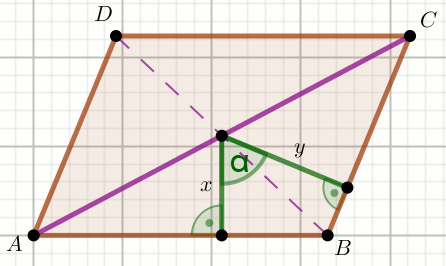

Oblicz jego pole powierzchni.
Dane
x=9=9.0000000000
y=6
\alpha=60^{\circ}=60
y=6
\alpha=60^{\circ}=60
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20150 |
Podpunkt 4.1 (2 pkt)
« Czworokąt na rysunku jest rombem, a jego przekątne mają długości
2x i 2y:
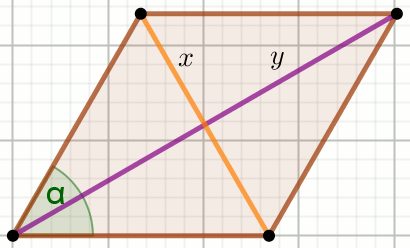

Oblicz \sin\alpha.
Dane
x=3
y=4
y=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20151 |
Podpunkt 5.1 (2 pkt)
« W równoległoboku przekątna BD ma długość
4, a kąty miary \alpha=45^{\circ}
i \beta=75^{\circ}:
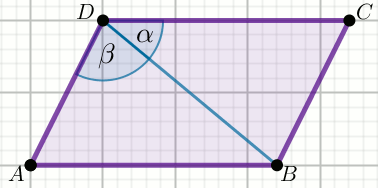

Oblicz pole powierzchni tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20152 |
Podpunkt 6.1 (2 pkt)
« Równoległobok ABCD ma kąt ostry o mierze
\alpha=30^{\circ} i bok
CD o długości 6.
Przez wierzchołki trójkąta ABD poprowadzono
okrąg o środku O i promieniu
r=3:
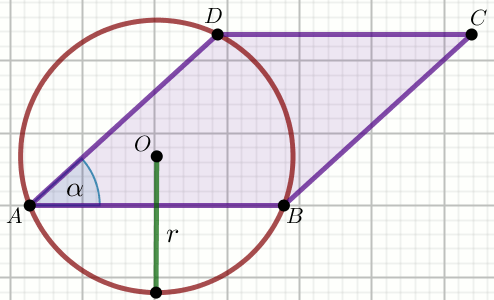

Oblicz pole powierzchni tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30117 |
Podpunkt 7.1 (4 pkt)
» Czworokąt ABCD na rysunku jest prostokątem,
a zielony czworokąt ma pole powierzchni równe P i
obwód równy L:
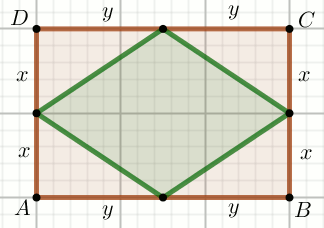

Oblicz obwód czworokąta ABCD.
Dane
P=3360
L=232
L=232
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30118 |
Podpunkt 8.1 (1 pkt)
» Czworokąt ABCD na rysunku jest rombem:
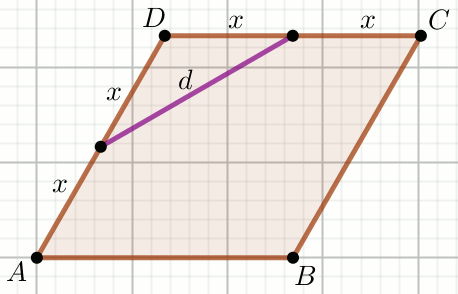

Oblicz długość krótszej przekątnej tego rombu.
Dane
d=6
P_{ABCD}=30
P_{ABCD}=30
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Oblicz długość obwodu tego rombu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.3 (1 pkt)
Oblicz długość wysokości tego rombu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.4 (1 pkt)
Wyznacz pole powierzchni mniejszej z figur, na które romb podzielił fioletowy
odcinek.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30119 |
Podpunkt 9.1 (2 pkt)
« Pole powierzchni rombu o wysokości h jest
równe P.
Oblicz długość krótszej przekątnej tego rombu.
Dane
h=\frac{3}{2}=1.500000000000000
P=3=3.000000000000000
P=3=3.000000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (2 pkt)
Oblicz długość dłuższej przekątnej tego rombu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30120 |
Podpunkt 10.1 (2 pkt)
« Czworokąt na rysunku jest równoległobokiem oraz
|PE|=3 i |PF|=6:
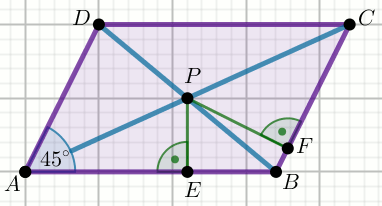

Oblicz jego pole powierzchni.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (2 pkt)
Oblicz |AC|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30121 |
Podpunkt 11.1 (2 pkt)
« Czworokąt na rysunku jest równoległobokiem, w którym:
|AC|=2\sqrt{7}, bok AB
jest o 2 dłuższy od boku AD,
zaś kąt \alpha ma miarę 120^{\circ}:
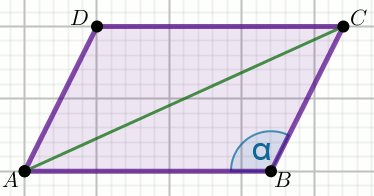

Oblicz jego pole powierzchni.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (2 pkt)
Oblicz |BD|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30122 |
Podpunkt 12.1 (2 pkt)
« Pole powierzchni rombu ABCD wynosi
P. Przekątne tego rombu wydłużono o
d_1 i d_2 i wówczas pole
powierzchni nowo otrzymanego rombu wzrosło o s.
Jaki obwód ma romb ABCD?
Podaj najmniejsze możliwe rozwiązanie.
Dane
P=480
d_1=4
d_2=10
s=220
d_1=4
d_2=10
s=220
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (2 pkt)
Podaj największe możliwe rozwiązanie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30123 |
Podpunkt 13.1 (2 pkt)
«« W równoległoboku wysokości mają długość
2 i 12.
Obwód tego równoległoboku ma długość 28.
Wyznacz długość dłuższego boku tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (2 pkt)
Oblicz cosinus kąta rozwartego jaki tworzą przekątne tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)