⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Wykres funkcji liczbowej
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- wykres funkcji
- interpretacja wykresu funkcji liczbowej
- punkty przecięcia wykresu funkcji z osiami
| Zadanie 1. 1 pkt ⋅ Numer: pp-10701 ⋅ Poprawnie: 197/472 [41%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Na rysunku przedstawiony jest fragment wykresu funkcji liniowej
f, przy czym
f(0)=-2 i f(1)=0.
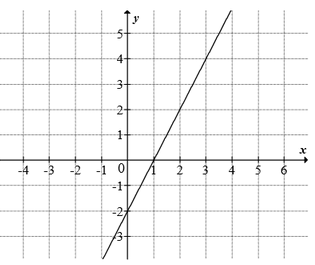
Wykres funkcji g jest symetryczny do wykresu funkcji f względem początku układu współrzędnych.
Funkcja g jest określona wzorem:
Odpowiedzi:
| A. g(x)=2x+2 | B. g(x)=-2x+2 |
| C. g(x)=-2x-2 | D. g(x)=2x-2 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10754 ⋅ Poprawnie: 260/431 [60%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt M o rzędnej równej 4
należy do wykresu funkcji f(x)=2+\frac{4}{1-x}.
Wyznacz odciętą punktu M.
Odpowiedź:
| x_M= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10757 ⋅ Poprawnie: 489/769 [63%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Do wykresu funkcji f należy punkt o współrzędnych
(7,1) oraz
f(8)=0.
Funkcja f opisana jest wzorem:
Odpowiedzi:
| A. f(x)=\frac{-2}{x} | B. f(x)=3x-2 |
| C. f(x)=-7x^2 | D. f(x)=\sqrt{-x+8} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10752 ⋅ Poprawnie: 357/577 [61%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Wykres funkcji y=\frac{77}{x} zawiera punkt o współrzędnych:
Odpowiedzi:
| A. \left(-\sqrt{7}, -11\sqrt{11}\right) | B. \left(\sqrt{77},-\sqrt{77}\right) |
| C. \left(-7,11\right) | D. \left(-7\sqrt{11}, -\sqrt{11}\right) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10734 ⋅ Poprawnie: 676/971 [69%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
» Do wykresu funkcji
f(x)=\frac{a}{x-1} należy punkt
A=\left(-4,\frac{8}{5}\right).
Wyznacz wartość parametru a.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10723 ⋅ Poprawnie: 204/342 [59%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Do wykresu funkcji f(x)=(m-1)x+m^2-5 należy punkt
P=(0,11).
Wyznacz wartość parametru m wiedząc, że jest ona dodatnia.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10739 ⋅ Poprawnie: 322/425 [75%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Punkt B=(3,y) należy do wykresu funkcji
f(x)=\frac{-3-x^2}{x-2}.
Wyznacz y.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10735 ⋅ Poprawnie: 277/402 [68%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Do wykresu funkcji określonej wzorem
f(x)=(m-8)x-1 należy punkt
S=(-5,29).
Wyznacz wartość parametru m.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10731 ⋅ Poprawnie: 402/921 [43%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji
y=f(x).
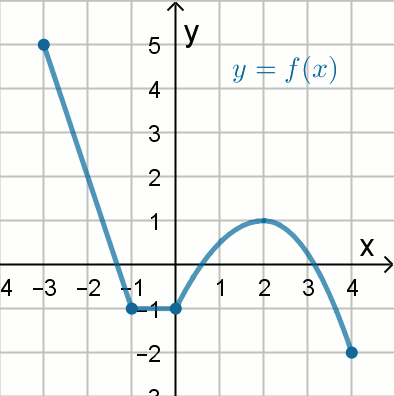
W którym z przedziałów, funkcja przyjmuje wartość 1:
Odpowiedzi:
| A. (-1,2) | B. \langle 2,4) |
| C. (2,3) | D. \langle 1,2) |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20293 ⋅ Poprawnie: 97/198 [48%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
» Dla jakich wartości parametru m\in\mathbb{R} wykresy funkcji
f(x)=\frac{2x+m}{x-9} oraz
g(x)=-1^{x-1} przecinają oś
Oy w tym samym punkcie.
Podaj najmniejszą możliwą wartość parametru m.
Odpowiedź:
| m_{min}= | |