⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Dziedzina funkcji liczbowej
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- dziedzina funkcji
- przeciwdziedzina
- warunki określoności funkcji
| Zadanie 1. 1 pkt ⋅ Numer: pp-10694 ⋅ Poprawnie: 487/767 [63%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Zbiór liczb rzeczywistych jest dziedziną funkcji:
Odpowiedzi:
| T/N : f(x)=\frac{x-1}{x^2} | T/N : f(x)=\sqrt{-x-1} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10682 ⋅ Poprawnie: 675/828 [81%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dziedziną funkcji f określonej wzorem
f(x)=\frac{x-4}{x^2-4x} może być zbiór:
Odpowiedzi:
| A. \mathbb{R} | B. \mathbb{R}-\{-4,4\} |
| C. \mathbb{R}-\{0,4\} | D. \mathbb{R}-\{-4,0\} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10688 ⋅ Poprawnie: 411/556 [73%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Wyznacz największą liczbę całkowitą należącą do dziedziny funkcji określonej wzorem
f(x)=\sqrt{30-\frac{2}{5}x}
.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10691 ⋅ Poprawnie: 387/764 [50%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wyznacz dziedzinę funkcji
f(x)=\frac{x+3}{\sqrt{4-x}}
i rozwiązanie zapisz w postaci sumy przedziałów. Liczba x_1
jest najmniejszm z końców liczbowych tych przedziałów, a liczba
x_2 jest największą liczbą całkowitą z dziedziny tej funkcji.
Podaj liczby x_1 i x_2.
Odpowiedzi:
| x_1 | = |
(wpisz liczbę całkowitą) |
| x_2 | = |
(wpisz liczbę całkowitą) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10690 ⋅ Poprawnie: 106/209 [50%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Wyznacz dziedzinę funkcji określonej wzorem
f(x)=\sqrt{x+4}\sqrt{x-10}
i zapisz rozwiązanie w postaci sumy przedziałów.
Liczba x_0 jest największym z końców liczbowych tych przedziałów.
Liczba m jest najmniejszą liczbą całkowitą z dziedziny tej funkcji.
Liczba x_0 jest największym z końców liczbowych tych przedziałów.
Liczba m jest najmniejszą liczbą całkowitą z dziedziny tej funkcji.
Podaj liczby x_0 i m.
Odpowiedzi:
| x_0 | = |
(wpisz liczbę całkowitą) |
| m | = |
(wpisz liczbę całkowitą) |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10689 ⋅ Poprawnie: 338/511 [66%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Dziedziną funkcji
f(x)=\frac{x}{\sqrt{9+x^2}}+(2-x)^2
jest:
Odpowiedzi:
| A. \mathbb{R}-\{-3,3\} | B. \mathbb{R} |
| C. (-\infty;-3)\cup(3;+\infty) | D. \mathbb{R}-\{-3\} |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10692 ⋅ Poprawnie: 127/169 [75%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Dziedziną funkcji f określonej wzorem
f(x)=\log{(x^2+16)}
jest zbiór:
Odpowiedzi:
| A. (-\infty;-4)\cup(4;+\infty) | B. \mathbb{R} |
| C. (-4;4) | D. \mathbb{R}-\{-4;4\} |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10693 ⋅ Poprawnie: 125/153 [81%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
» Do dziedziny funkcji
f(x)=\log(36-x^2)
należy liczba:
Odpowiedzi:
| A. \sqrt{38} | B. 8 |
| C. -\sqrt{37} | D. -\sqrt{35} |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10681 ⋅ Poprawnie: 639/895 [71%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Wyznacz dziedzinę D_f funkcji określonej wzorem
f(x)=\sqrt{-x-7}
.
Podaj największą liczbę całkowitą, która należy do zbioru D_f.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 10. 1 pkt ⋅ Numer: pp-10687 ⋅ Poprawnie: 305/500 [61%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Wyznacz dziedzinę D_f funkcji określonej wzorem
f(x)=\sqrt{7-x}-\sqrt{15-x}
.
Podaj największą liczbę całkowitą, która należy do zbioru D_f.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 11. 1 pkt ⋅ Numer: pp-10686 ⋅ Poprawnie: 326/516 [63%] | Rozwiąż |
Podpunkt 11.1 (0.8 pkt)
Dziedziną funkcji g(x)=\sqrt{4-\frac{4x-10}{2}}
jest pewien przedział.
Podaj ten koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 11.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. -4 | B. -6 |
| C. 0 | D. -2 |
| E. -\infty | F. +\infty |
| Zadanie 12. 1 pkt ⋅ Numer: pp-10684 ⋅ Poprawnie: 164/246 [66%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Dla którego z podanych zbiorów liczb naturalnych wyrażenie
\frac{\sqrt{x-4}}{x-6}
ma sens liczbowy:
Odpowiedzi:
| A. \{4,7\} | B. \{3,4,7\} |
| C. \{5,6,10\} | D. \{0,4,9\} |
| Zadanie 13. 1 pkt ⋅ Numer: pp-10683 ⋅ Poprawnie: 999/1113 [89%] | Rozwiąż |
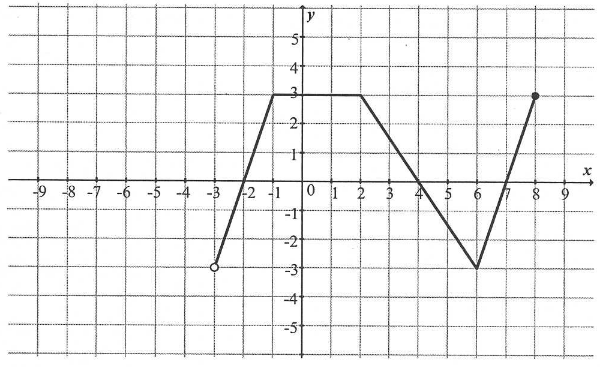
Podpunkt 13.1 (1 pkt)
Dziedziną funkcji f jest przedział:
Odpowiedzi:
| A. \langle -3, 3\rangle | B. \langle 0, 3\rangle |
| C. (0, 8\rangle | D. (-3, 8\rangle |
| Zadanie 14. 2 pkt ⋅ Numer: pp-20767 ⋅ Poprawnie: 161/340 [47%] | Rozwiąż |
Podpunkt 14.1 (2 pkt)
«« Wyznacz dziedzinę funkcji:
f(x)=\frac{x-4}{9x^2+24x+16}+\frac{1}{9x^2-16}
.
Podaj sumę tych wszystkich wartości ujemnych x, które nie należą do dziedziny tej funkcji.
Odpowiedź:
| suma_{x\lessdot 0, x\notin D_f}= | |
| Zadanie 15. 2 pkt ⋅ Numer: pp-20768 ⋅ Poprawnie: 273/804 [33%] | Rozwiąż |
Podpunkt 15.1 (2 pkt)
Wyznacz dziedzinę funkcji:
f(x)=\frac{\sqrt{x+7}}{x+4}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 16. 2 pkt ⋅ Numer: pp-20771 ⋅ Poprawnie: 211/583 [36%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
« Wyznacz dziedzinę funkcji:
f(x)=\frac{\sqrt{x+12}}{\sqrt{18-x}}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
Ile liczb całkowitych jedno lub dwucyfrowych należy do dziedziny
tej funkcji.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 17. 2 pkt ⋅ Numer: pp-20772 ⋅ Poprawnie: 203/572 [35%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
« Wyznacz dziedzinę funkcji:
f(x)=\frac{2x}{6x-2}+\sqrt{x+2}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Ile jest tych przedziałów?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 17.2 (1 pkt)
Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
| \frac{m}{n}= | |