Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Funkcja liniowa i jej wykres

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-10936 ⋅ Poprawnie: 849/1227 [69%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 « Dana jest funkcja liniowa określona wzorem f(x)=5x-10.

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : funkcja f rośnie w \mathbb{R} T/N : miejscem zerowym tej funkcji jest liczba 2
T/N : do jej wykresu należy punkt (-1,15)  
Zadanie 2.  1 pkt ⋅ Numer: pp-10937 ⋅ Poprawnie: 665/982 [67%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 Dana jest funkcja liniowa f(x)=-4x+2.

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : funkcja f jest malejąca w zbiorze \mathbb{R} T/N : miejscem zerowym tej funkcji jest liczba -\frac{1}{2}
T/N : wykres tej funkcji przecina oś rzednych w punkcie (0,2)  
Zadanie 3.  1 pkt ⋅ Numer: pp-10943 ⋅ Poprawnie: 116/193 [60%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 » Wiedząc, że h(x)=3\sqrt{3}-6x oblicz h\left(\frac{3\sqrt{3}-9}{6}\right).

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : liczba ta jest złożona T/N : liczba ta jest niewymierna
Zadanie 4.  1 pkt ⋅ Numer: pp-10813 ⋅ Poprawnie: 211/390 [54%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
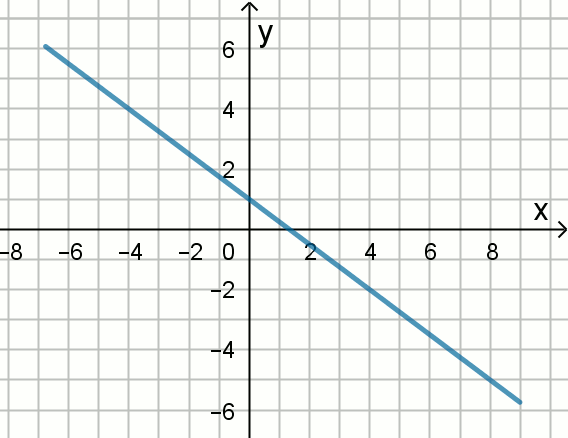
Proste pokazane na rysunku
określone są równaniami 2x-4y=a, 3x+y=b i 3x+8y=c.

Wyznacz współczynniki a, b i c.

Odpowiedzi:
a= (wpisz liczbę całkowitą)
b= (wpisz liczbę całkowitą)
c= (wpisz liczbę całkowitą)
Zadanie 5.  1 pkt ⋅ Numer: pp-10814 ⋅ Poprawnie: 268/528 [50%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
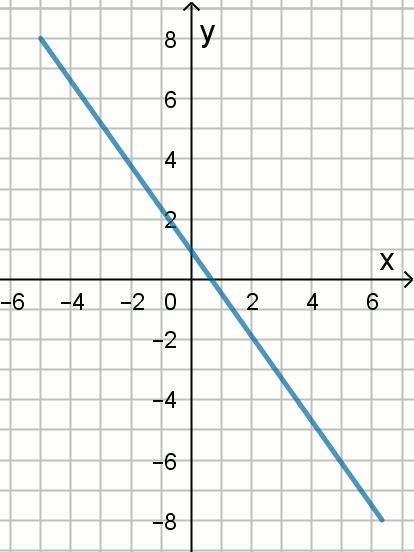
 » Na rysunku przedstawiono wykres prostej:
Prosta symetryczna do tej prostej względem osi Ox określona jest równaniem ax+by=4.

Podaj współczynniki a i b.

Odpowiedzi:
a= (wpisz liczbę całkowitą)
b= (wpisz liczbę całkowitą)
Zadanie 6.  1 pkt ⋅ Numer: pp-10815 ⋅ Poprawnie: 559/825 [67%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 Funkcja liniowa f określona jest wzorem f(x)=mx+n. Funkcja ta spełnia warunek f(2)=-6, a jej wykres zawiera punkt (1,5).

Wyznacz współczynniki m i n.

Odpowiedzi:
m= (dwie liczby całkowite)
n= (dwie liczby całkowite)
Zadanie 7.  1 pkt ⋅ Numer: pp-10817 ⋅ Poprawnie: 129/219 [58%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 « Dane są funkcje f(x)=-2x-3 oraz g(x)=f(x-1)+4. Zapisz wzór funkcji g w postaci g(x)=ax+b.

Podaj współczynniki a i b.

Odpowiedzi:
a= (wpisz liczbę całkowitą)
b= (wpisz liczbę całkowitą)
Zadanie 8.  1 pkt ⋅ Numer: pp-10818 ⋅ Poprawnie: 196/339 [57%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 Do wykresu funkcji liniowej f należą punkty A=(4, 0) i B=(0,7). Wykres funkcji liniowej g określonej wzorem g(x)=mx+n jest symetryczny do wykresu funkcji f względem osi Ox.

Wyznacz współczynniki m i n.

Odpowiedzi:
m= (dwie liczby całkowite)
n= (wpisz liczbę całkowitą)
Zadanie 9.  1 pkt ⋅ Numer: pp-10816 ⋅ Poprawnie: 227/429 [52%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Prosta wyznaczona przez punkty A=(-2,-6) i B=(2,2) określona jest równaniem 8x+by+c=0.

Podaj liczby b i c.

Odpowiedzi:
b= (wpisz liczbę całkowitą)
c= (wpisz liczbę całkowitą)
Zadanie 10.  1 pkt ⋅ Numer: pp-10802 ⋅ Poprawnie: 436/609 [71%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 Punkty A=(6,-7) i B=(-6,13) należą do prostej o równaniu 5x+by+c=0.

Wyznacz liczby b i c.

Odpowiedzi:
b= (wpisz liczbę całkowitą)
c= (wpisz liczbę całkowitą)
Zadanie 11.  1 pkt ⋅ Numer: pp-11418 ⋅ Poprawnie: 172/288 [59%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 » Punkty A=(3,5) i B=(-3,11) należą do prostej k. Prosta l symetryczna do prostej k względem początku układu współrzędnych ma równanie y=ax+b.

Wyznacz liczby a i b.

Odpowiedzi:
a= (wpisz liczbę całkowitą)
b= (wpisz liczbę całkowitą)
Zadanie 12.  1 pkt ⋅ Numer: pp-10944 ⋅ Poprawnie: 289/476 [60%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 Funkcja f jest określona wzorem f(x)=4x-\frac{1}{2} dla każdej liczby z przedziału \langle -4,0\rangle. Zbiorem wartości tej funkcji jest przedział \langle p, q\rangle.

Podaj liczby p i q.

Odpowiedzi:
p= (dwie liczby całkowite)
q= (dwie liczby całkowite)
Zadanie 13.  1 pkt ⋅ Numer: pp-10809 ⋅ Poprawnie: 98/159 [61%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 « Punkt o współrzędnych (9-3t, 2t+2), gdzie t\in\mathbb{R}, należy do prostej określonej równaniem 2x+by=c.

Wyznacz współczynniki b i c.

Odpowiedzi:
b= (wpisz liczbę całkowitą)
c= (wpisz liczbę całkowitą)
Zadanie 14.  1 pkt ⋅ Numer: pp-10807 ⋅ Poprawnie: 530/709 [74%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
 Współczynnik kierunkowy prostej, do której należą punkty A=(17,13) i B=(12,48) jest równy m.

Podaj m.

Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Zadanie 15.  1 pkt ⋅ Numer: pp-10811 ⋅ Poprawnie: 517/717 [72%] Rozwiąż 
Podpunkt 15.1 (1 pkt)
 Do prostej o równaniu y=ax+b należą punkty P=(1,-7) i Q=(8,-5).

Wyznacz współczynnik a.

Odpowiedź:
a=
(wpisz dwie liczby całkowite)
Zadanie 16.  1 pkt ⋅ Numer: pp-10808 ⋅ Poprawnie: 198/382 [51%] Rozwiąż 
Podpunkt 16.1 (1 pkt)
 Na rysunku przedstawiono wykres funkcji y=f(x):
Wskaż wzór funkcji, której wykres jest symetryczny do tego wykresu względem osi Ox:
Odpowiedzi:
A. y=\sqrt{3}x-1 B. y=-\frac{\sqrt{3}}{3}x+1
C. y=\sqrt{3}x+1 D. y=\frac{1}{\sqrt{3}}x+1
Zadanie 17.  1 pkt ⋅ Numer: pp-10810 ⋅ Poprawnie: 107/166 [64%] Rozwiąż 
Podpunkt 17.1 (1 pkt)
 Punkt o współrzędnych (2t-3, 4t+2), gdzie t\in\mathbb{R}, należy do prostej określonej równaniem y=2x+b.

Wyznacz współczynnik b.

Odpowiedź:
b= (wpisz liczbę całkowitą)
Zadanie 18.  1 pkt ⋅ Numer: pp-10940 ⋅ Poprawnie: 40/66 [60%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
 « Wykres funkcji liniowej h(x)=(p-9)x+2 przechodzi przez punkt S, którego obie współrzędne są nieparzyste.

Liczba p może być równa:

Odpowiedzi:
A. 1 B. 9
C. -3 D. -1
E. 10 F. -5
Zadanie 19.  1 pkt ⋅ Numer: pp-10806 ⋅ Poprawnie: 280/548 [51%] Rozwiąż 
Podpunkt 19.1 (1 pkt)
 Funkcja liniowa f(x)=(m+2)x-(m+1)^2+29 jest malejąca i jej wykres przecina oś rzędnych w punkcie P=(0,-35).

Wyznacz m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 20.  1 pkt ⋅ Numer: pp-10805 ⋅ Poprawnie: 276/542 [50%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
 Funkcja liniowa spełnia warunki f(-\sqrt{2})=1 i f(9\sqrt{2})=-8.

Wynika z tego, że jej wykres przechodzi przez ćwiartki układu:

Odpowiedzi:
A. I, II i III B. I, III i IV
C. II, III i IV D. I, II i IV
Zadanie 21.  1 pkt ⋅ Numer: pp-10928 ⋅ Poprawnie: 325/483 [67%] Rozwiąż 
Podpunkt 21.1 (1 pkt)
 Wykres funkcji liniowej y=\frac{1}{5}x+9 przecina osie układu współrzędnych w punktach A i B.

Oblicz pole powierzchni trójkąta AOB.

Odpowiedź:
P_{AOB}=
(wpisz dwie liczby całkowite)
Zadanie 22.  1 pkt ⋅ Numer: pp-11406 ⋅ Poprawnie: 504/694 [72%] Rozwiąż 
Podpunkt 22.1 (0.5 pkt)
 Miejscem zerowym funkcji liniowej f(x)=3(x+5)-6\sqrt{3} jest liczba a+b\sqrt{3}.

Podaj a.

Odpowiedź:
a= (wpisz liczbę całkowitą)
Podpunkt 22.2 (0.5 pkt)
 Podaj b.
Odpowiedź:
b= (wpisz liczbę całkowitą)
Zadanie 23.  1 pkt ⋅ Numer: pp-10793 ⋅ Poprawnie: 524/662 [79%] Rozwiąż 
Podpunkt 23.1 (1 pkt)
 Liczba ......... jest miejscem zerowym funkcji określonej wzorem f(x)=\frac{1}{5}x+\frac{4}{5}.

Podaj brakującą liczbę.

Odpowiedź:
\frac{m}{n}=
(wpisz dwie liczby całkowite)
Zadanie 24.  1 pkt ⋅ Numer: pp-10794 ⋅ Poprawnie: 354/493 [71%] Rozwiąż 
Podpunkt 24.1 (1 pkt)
 Wyznacz miejsce zerowe funkcji określonej wzorem f(x)=\frac{4}{5}-\frac{1}{5}x.
Odpowiedź:
\frac{m}{n}=
(wpisz dwie liczby całkowite)
Zadanie 25.  1 pkt ⋅ Numer: pp-10795 ⋅ Poprawnie: 454/762 [59%] Rozwiąż 
Podpunkt 25.1 (1 pkt)
 Funkcja liniowa określona wzorem y=mx+n, wartości ujemne przyjmuje tylko w przedziale (-5,+\infty). Wykres tej funkcji przecina oś Oy w punkcie (0,-8).

Wyznacz współczynniki m i n.

Odpowiedzi:
m= (dwie liczby całkowite)
n= (wpisz liczbę całkowitą)
Zadanie 26.  1 pkt ⋅ Numer: pp-11431 ⋅ Poprawnie: 334/513 [65%] Rozwiąż 
Podpunkt 26.1 (1 pkt)
 Liczba -7 jest miejscem zerowym funkcji liniowej f(x)=.....\cdot x+b, a punkt M=(6,26) należy do wykresu tej funkcji.

Podaj brakującą liczbę.

Odpowiedź:
Wpisz odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 27.  1 pkt ⋅ Numer: pp-10922 ⋅ Poprawnie: 545/706 [77%] Rozwiąż 
Podpunkt 27.1 (1 pkt)
 Dana jest funkcja liniowa f(x)=-\frac{5}{8}-\frac{1}{7}x.

Wyznacz miejsce zerowe tej funkcji.

Odpowiedź:
x=
(wpisz dwie liczby całkowite)
Zadanie 28.  1 pkt ⋅ Numer: pp-10933 ⋅ Poprawnie: 302/535 [56%] Rozwiąż 
Podpunkt 28.1 (1 pkt)
 » Wykresy funkcji f(x)=-\frac{4}{5}x-5 oraz g(x)=mx+2 przecinają oś Ox w tym samym punkcie.

Wyznacz m.

Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Zadanie 29.  1 pkt ⋅ Numer: pp-10941 ⋅ Poprawnie: 163/214 [76%] Rozwiąż 
Podpunkt 29.1 (1 pkt)
 Dana jest funkcja liniowa określona wzorem g(x)=(\sqrt{17}+\sqrt{13})x-4 . Miejscem zerowym funkcji g jest liczba \frac{\sqrt{13}-\sqrt{17}}{......}.

Podaj brakującą liczbę.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 30.  1 pkt ⋅ Numer: pp-10945 ⋅ Poprawnie: 78/136 [57%] Rozwiąż 
Podpunkt 30.1 (1 pkt)
 Miejscem zerowym funkcji określonej wzorem f(x)=7\sqrt{13}x-\frac{\sqrt{143}}{2} jest liczba \frac{\sqrt{13\cdot 143}}{......}.

Podaj brakującą liczbę.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 31.  1 pkt ⋅ Numer: pp-10923 ⋅ Poprawnie: 157/248 [63%] Rozwiąż 
Podpunkt 31.1 (0.2 pkt)
 Miejsce zerowe funkcji liniowej określonej wzorem f(x)=7x-5m jest większe od 2 dla każdej liczby m należącej do pewnego przedziału.

Przedział ten ma postać:

Odpowiedzi:
A. (p,+\infty) B. (-\infty,q\rangle
C. (-\infty,q) D. \langle p,q\rangle
E. \langle p,+\infty) F. (p,q)
Podpunkt 31.2 (0.8 pkt)
 Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Zadanie 32.  1 pkt ⋅ Numer: pp-10796 ⋅ Poprawnie: 152/254 [59%] Rozwiąż 
Podpunkt 32.1 (1 pkt)
 « Liczba -4 jest miejscem zerowym funkcji określonej wzorem f(x)=\left(1+\frac{a}{8}\right)x+2.

Wyznacz a.

Odpowiedź:
a=
(wpisz dwie liczby całkowite)
Zadanie 33.  1 pkt ⋅ Numer: pp-10792 ⋅ Poprawnie: 218/295 [73%] Rozwiąż 
Podpunkt 33.1 (1 pkt)
 Wykres funkcji g(x)=(m+2)x+15 przecina oś Ox w punkcie o odciętej równej \frac{\log_{2}{8}}{3^0}.

Wyznacz m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 34.  1 pkt ⋅ Numer: pp-11503 ⋅ Poprawnie: 661/948 [69%] Rozwiąż 
Podpunkt 34.1 (1 pkt)
 Funkcje liniowe określone wzorami f(x)=-\frac{4}{5}x-5 oraz g(x)=mx+2 mają wspólne miejsce zerowe.

Wyznacz m.

Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Zadanie 35.  1 pkt ⋅ Numer: pp-11764 ⋅ Poprawnie: 746/919 [81%] Rozwiąż 
Podpunkt 35.1 (1 pkt)
 Punkt A=(11,16) należy do obu prostych k i l. Prosta k przecina oś Oy w punkcie o rzędnej -6, zas prosta l przecina oś Oy w punkcie o rzędnej 5.

Wskaż układ równań, którego interpretację opisano powyżej:

Odpowiedzi:
A. \begin{cases}y=2x-6\\y=x+5\end{cases} B. \begin{cases}y=-2x+6\\y=x+5\end{cases}
C. \begin{cases}y=-2x-6\\y=x-5\end{cases} D. \begin{cases}y=2x-6\\y=-x-5\end{cases}
Zadanie 36.  1 pkt ⋅ Numer: pp-11812 ⋅ Poprawnie: 582/718 [81%] Rozwiąż 
Podpunkt 36.1 (1 pkt)
 Miejscem zerowym funkcji liniowej f jest liczba 5. Wykres tej funkcji zawiera punkt o współrzędnych (1,5).

Wzór funkcji f ma postać

Odpowiedzi:
A. f(x)=-\frac{5}{4}x+\frac{29}{4} B. f(x)=\frac{5}{8}x+\frac{25}{4}
C. f(x)=-\frac{5}{2}x+\frac{25}{4} D. f(x)=-\frac{5}{4}x+\frac{25}{4}
Zadanie 37.  1 pkt ⋅ Numer: pp-11835 ⋅ Poprawnie: 504/665 [75%] Rozwiąż 
Podpunkt 37.1 (1 pkt)
 Funkcja liniowa f jest określona wzorem f(x)=-\frac{1}{22}x+\frac{7}{11}.

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : miejscem zerowym funkcji f jest liczba 14 T/N : do wykresu funkcji f należy punkt \left(33,-\frac{41}{22}\right)
Zadanie 38.  1 pkt ⋅ Numer: pp-11859 ⋅ Poprawnie: 256/360 [71%] Rozwiąż 
Podpunkt 38.1 (1 pkt)
 Miejscem zerowym funkcji liniowej f określonej wzorem f(x)=-\frac{1}{5}(x+3)-3 jest liczba:
Odpowiedzi:
A. -12 B. -36
C. -27 D. -18
E. -9 F. -6
Zadanie 39.  1 pkt ⋅ Numer: pp-11887 ⋅ Poprawnie: 161/177 [90%] Rozwiąż 
Podpunkt 39.1 (1 pkt)
 Punkt M=(3, -2) należy do wykresu funkcji liniowej f określonej wzorem f(x)=5x+b-1.

Wynika stąd, że b jest równe:

Odpowiedzi:
A. -24 B. -16
C. -21 D. -22
E. -13 F. -10
Zadanie 40.  1 pkt ⋅ Numer: pp-11949 ⋅ Poprawnie: 103/119 [86%] Rozwiąż 
Podpunkt 40.1 (1 pkt)
 Na płaszczyźnie, w kartezjańskim układzie współrzędnych (x,y), dana jest prosta k o równaniu y=3x+b, przechodząca przez punkt A=(5,17). Współczynnik b w równaniu tej prostej jest równy:
Odpowiedzi:
A. 5 B. 2
C. 1 D. -5
E. -2 F. 4
G. -3  
Zadanie 41.  1 pkt ⋅ Numer: pp-11990 ⋅ Poprawnie: 487/628 [77%] Rozwiąż 
Podpunkt 41.1 (1 pkt)
 Funkcje liniowe f oraz g, określone wzorami f(x)=-3x-1 oraz g(x)=ax-1, mają to samo miejsce zerowe.

Współczynnik a we wzorze funkcji g jest równy:

Odpowiedzi:
A. \frac{9}{4} B. 4
C. \frac{9}{2} D. -\frac{9}{2}
E. -6 F. -4
G. -\frac{9}{4} H. -3
Zadanie 42.  1 pkt ⋅ Numer: pp-12012 ⋅ Poprawnie: 390/473 [82%] Rozwiąż 
Podpunkt 42.1 (1 pkt)
 Liczba 2 jest miejscem zerowym funkcji liniowej f(x)=(-8-m)x+4.

Liczba m jest równa:

Odpowiedzi:
A. 0 B. 1
C. -13 D. -8
E. -1 F. -15
G. -14 H. -6
I. -4 J. 2
Zadanie 43.  1 pkt ⋅ Numer: pp-12031 ⋅ Poprawnie: 58/68 [85%] Rozwiąż 
Podpunkt 43.1 (1 pkt)
 Funkcja liniowa f(x)=(a+8)x+8 osiąga wartość największą równą 8.

Wtedy a jest równe:

Odpowiedzi:
A. -5 B. -13
C. -8 D. -2
E. -4 F. -12
Zadanie 44.  1 pkt ⋅ Numer: pp-12114 ⋅ Poprawnie: 42/49 [85%] Rozwiąż 
Podpunkt 44.1 (1 pkt)
 Funkcja f określona jest wxorem f(x)=ax+8 dla każdej liczby rzeczywistej x. Miejscem zerowym funkcji f jest liczba \frac{9}{2}.

Wtedy a jest równe:

Odpowiedzi:
A. -\frac{8}{9} B. \frac{8}{9}
C. \frac{32}{27} D. -\frac{32}{27}
E. -\frac{8}{3} F. \frac{32}{9}
G. \frac{4}{9} H. -\frac{16}{9}
Zadanie 45.  1 pkt ⋅ Numer: pp-12115 ⋅ Poprawnie: 17/28 [60%] Rozwiąż 
Podpunkt 45.1 (1 pkt)
 Prosta k przechodzi przez punkt A=(-4,4) i jest nachylona do osi Ox pod kątem 45^{\circ}.

Prosta k ma równanie:

Odpowiedzi:
A. y=x+10 B. y=x+11
C. y=x+9 D. y=-x+6
E. y=-x+10 F. y=x+8
G. y=x+7 H. y=x+6
Zadanie 46.  1 pkt ⋅ Numer: pp-12389 ⋅ Poprawnie: 393/410 [95%] Rozwiąż 
Podpunkt 46.1 (1 pkt)
 Funkcja liniowa f jest określona wzorem f(x)=(6+6m)x-6.

Funkcja ta nie ma miejsca zerowego dla m równego:

Odpowiedzi:
A. -\frac{1}{3} B. -1
C. \frac{2}{3} D. -\frac{4}{3}
E. -\frac{1}{2} F. -\frac{3}{2}
G. -2 H. 2
Zadanie 47.  1 pkt ⋅ Numer: pp-12408 ⋅ Poprawnie: 288/302 [95%] Rozwiąż 
Podpunkt 47.1 (1 pkt)
 Funkcja liniowa f jest określona wzorem f(x)=\frac{1}{2}x-k-11, gdzie k jest liczbą rzeczywistą. Miejsce zerowe funkcji f jest liczbą większą od 2.

Liczba k należy do przedziału:

Odpowiedzi:
A. (-18,-14) B. (-\infty,-18)
C. (-14,-13) D. (-11,-10)
E. (-13,-11) F. (-10,+\infty)
Zadanie 48.  2 pkt ⋅ Numer: pp-20306 ⋅ Poprawnie: 203/651 [31%] Rozwiąż 
Podpunkt 48.1 (1 pkt)
 « Dane są punkty A=(-6, 11) i B=(6, -49). Wyznacz równanie prostej AB.

Podaj współczynnik kierunkowy tej prostej.

Odpowiedź:
a= (wpisz liczbę całkowitą)
Podpunkt 48.2 (1 pkt)
 Wyznacz odciętą punktu przecięcia prostej AB z osią Ox.
Odpowiedź:
x_0=
(wpisz dwie liczby całkowite)
Zadanie 49.  2 pkt ⋅ Numer: pp-20307 ⋅ Poprawnie: 44/104 [42%] Rozwiąż 
Podpunkt 49.1 (1 pkt)
 » Funkcja liniowa określona wzorem g(x)=ax+b spełnia warunki: \begin{cases} g(-2)=16 \\ g(x)\lessdot 0 \iff x\in(2,+\infty) \end{cases} .

Podaj a.

Odpowiedź:
a=
(wpisz dwie liczby całkowite)
Podpunkt 49.2 (1 pkt)
 Podaj b.
Odpowiedź:
b=
(wpisz dwie liczby całkowite)
Zadanie 50.  2 pkt ⋅ Numer: pp-20308 ⋅ Poprawnie: 232/418 [55%] Rozwiąż 
Podpunkt 50.1 (2 pkt)
 Miejscem zerowym funkcji f(x)=\frac{2-7m}{2}x+2 jest liczba \frac{1}{24}.

Wyznacz m.

Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Zadanie 51.  2 pkt ⋅ Numer: pp-20309 ⋅ Poprawnie: 231/298 [77%] Rozwiąż 
Podpunkt 51.1 (2 pkt)
 » Oblicz miejsce zerowe funkcji f(x)= \begin{cases} 2+2x \text{, dla } x\leqslant 2 \\ x \text{, dla } x > 2 \end{cases} .
Odpowiedź:
x=
(wpisz dwie liczby całkowite)
Zadanie 52.  2 pkt ⋅ Numer: pp-20840 ⋅ Poprawnie: 156/279 [55%] Rozwiąż 
Podpunkt 52.1 (1 pkt)
 « Funkcja liniowa f określona wzorem f(x)=mx+n wartości nieujemne przyjmuje tylko w przedziale (-\infty, 5\rangle oraz zachodzi warunek f(-2)=7. Wyznacz wartości współczynników m i n.

Podaj m.

Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Podpunkt 52.2 (1 pkt)
 Podaj n.
Odpowiedź:
n=
(wpisz dwie liczby całkowite)
Zadanie 53.  2 pkt ⋅ Numer: pp-20844 ⋅ Poprawnie: 113/329 [34%] Rozwiąż 
Podpunkt 53.1 (1 pkt)
 « Punkt K=(-2,6) należy do wykresu funkcji liniowej określonej wzorem f(x)=(2-m)x+4.

Wyznacz m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Podpunkt 53.2 (1 pkt)
 Wykresy funkcji f i funkcji określonej wzorem h(x)=2-2x przecinają oś Ox w tym samym punkcie.

Podaj m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 54.  2 pkt ⋅ Numer: pp-20846 ⋅ Poprawnie: 144/221 [65%] Rozwiąż 
Podpunkt 54.1 (2 pkt)
 « Liczba b spełnia równanie (b+5)(b-1)=(b+2)(b+11)-3(b+3).

Podaj miejsce zerowe funkcji f(x)=2x+b.

Odpowiedź:
x=
(wpisz dwie liczby całkowite)
Zadanie 55.  2 pkt ⋅ Numer: pp-20845 ⋅ Poprawnie: 55/95 [57%] Rozwiąż 
Podpunkt 55.1 (2 pkt)
 « Liczba b spełnia równanie (b+2-\sqrt{2})^2-(b+2-2\sqrt{2})^2=-6.

Podaj miejsce zerowe funkcji określonej wzorem f(x)=2x+b.

Odpowiedź:
x=
(wpisz dwie liczby całkowite)
Zadanie 56.  2 pkt ⋅ Numer: pp-20847 ⋅ Poprawnie: 156/296 [52%] Rozwiąż 
Podpunkt 56.1 (2 pkt)
 « Liczba b spełnia równanie (b+2)(2-b)+(1+b)^2=0.

Podaj miejsce zerowe funkcji określonej wzorem f(x)=2x+b.

Odpowiedź:
x=
(wpisz dwie liczby całkowite)
Zadanie 57.  2 pkt ⋅ Numer: pp-20298 ⋅ Poprawnie: 223/632 [35%] Rozwiąż 
Podpunkt 57.1 (1 pkt)
 « Funkcja liniowa f określona jest wzorem f(x)=mx-n. Wiadomo, że f(6)=-2, oraz, że do wykresu funkcji f należy punkt P=(-6,4).

Wyznacz m.

Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Podpunkt 57.2 (1 pkt)
 Wyznacz n.
Odpowiedź:
n=
(wpisz dwie liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm