⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Funkcja liniowa i jej wykres
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- funkcja liniowa
- wykres funkcji liniowej
- prosta na płaszczyźnie
| Zadanie 1. 1 pkt ⋅ Numer: pr-10104 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Na rysunku poniżej przedstawiony jest fragment wykresu funkcji liniowej
y=ax+b.
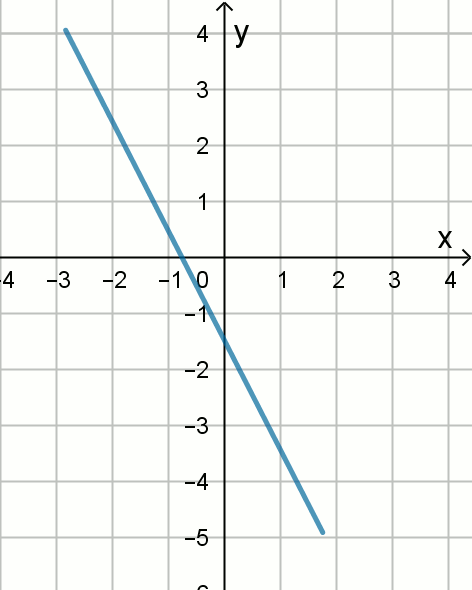
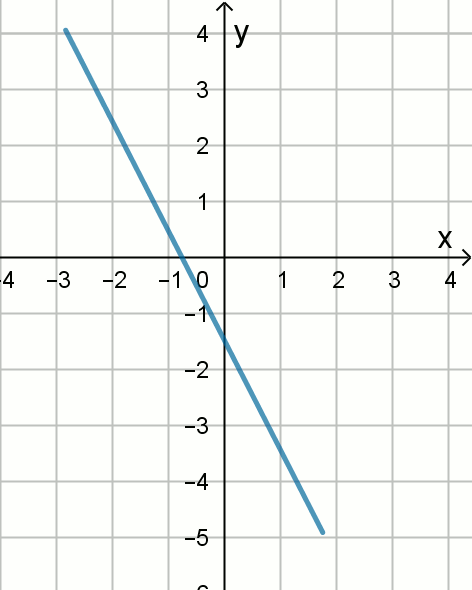
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : a > -1 \wedge b \lessdot -1 | T/N : a \lessdot -1 \wedge b \lessdot -1 |
| Zadanie 2. 1 pkt ⋅ Numer: pr-10103 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Na rysunku przedstawiony jest fragment wykresu funkcji liniowej
f, przy czym
f(0)=-2 i
f(-4)=0.
Wykres funkcji określonej wzorem g(x)=ax+b jest symetryczny do wykresu funkcji f względem prostej o równaniu y=x.
Wyznacz współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. 1 pkt ⋅ Numer: pr-10474 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Na rysunku przedstawiony jest fragment wykresu funkcji liniowej
f, przy czym
f(0)=-2 i
f(-4)=0.
Wykres funkcji określonej wzorem g(a)=ax+b jest symetryczny do wykresu funkcji f względem prostej y=-x.
Wyznacz współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 4. 1 pkt ⋅ Numer: pr-10416 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Funkcja f określona jest wzorem:
f(x)=\left\lbrace
\begin{array}{ll}
\frac{2}{3}x-2 & \text{dla }x \leqslant -3\\
-4 & \text{dla }x\in(-3,2)\\
-x & \text{dla }x\geqslant 2
\end{array}
.
Funkcja ta jest rosnąca w przedziale:
Odpowiedzi:
| A. \langle 2,+\infty) | B. (-\infty,2) |
| C. (-\infty, -3\rangle | D. (-3,2\rangle |
| Zadanie 5. 1 pkt ⋅ Numer: pr-10107 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Funkcja f:\mathbb{R}\to\mathbb{R} jest funkcją
liniową malejącą taką, że
f\left(-\frac{1}{3}\right)=0. Funkcja g
określona jest wzorem
g(x)=f\left(-\frac{3}{2}+x\right).
Wyznacz miejsce zerowe funkcji g.
Odpowiedź:
| x= | |
| Zadanie 6. 2 pkt ⋅ Numer: pr-20449 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 6.1 (2 pkt)
« Wyznacz współczynnik kierunkowy m prostej przechodzącej przez
punkty A=(-3-\sqrt{5},2-4\sqrt{5}) oraz
B=(\sqrt{5}-2,3).
Podaj m.
Odpowiedź:
| m= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 7. 2 pkt ⋅ Numer: pr-20450 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Dane są funkcje
f(x)=
\begin{cases}
-1\text{, dla }x\leqslant 2 \\
x+1\text{, dla }x > 2
\end{cases}
oraz g(x)=-f(-x).
Oblicz 100\cdot \left|g(-\sqrt{5})\cdot g(-\sqrt{3})\cdot g(-\sqrt{2})\right| .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20032 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=ax+b. Dla a=698
i b=699 oblicz
\frac{f(699)}{699^2}.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Narysuj w układzie współrzędnych zbiór
A=\left\{(x,y): x\in\langle 1,3\rangle \wedge y=-\frac{1}{2}x+b \wedge b\in\langle -4,1\rangle\right\}
.
Podaj współrzędną y tego punktu należącego do zbioru A, który jest najbardziej oddalony od początku układu współrzędnych.
Odpowiedź:
| y= | |