Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Znaczenie współczynników we wzorze funkcji liniowej

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-10899 ⋅ Poprawnie: 85/117 [72%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 Punkty o współrzędnych (400,100) oraz (600,-400) należą do wykresu funkcji liniowej y=mx+n.

Oceń prawdziwość poniższych zdań:

Odpowiedzi:
T/N : z treści wynika, że n=0 T/N : z treści wynika, że m \lessdot 0
T/N : z treści wynika, że n \lessdot 0  
Zadanie 2.  1 pkt ⋅ Numer: pp-11429 ⋅ Poprawnie: 431/577 [74%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 Funkcja liniowa f określona jest wzorem f(x)=-\frac{1}{4}x-4 i przecina oś Oy w punkcie P.

Które z poniższych zdań są prawdziwe?

Odpowiedzi:
T/N : funkcja ta jest malejąca i P=\left(0,1\right) T/N : funkcja ta jest malejąca i P=\left(0,4\right)
T/N : funkcja ta jest malejąca i P=\left(0,-4\right)  
Zadanie 3.  1 pkt ⋅ Numer: pp-10900 ⋅ Poprawnie: 137/214 [64%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 Proporcjonalnością prostą jest zależność opisana wzorem:
Odpowiedzi:
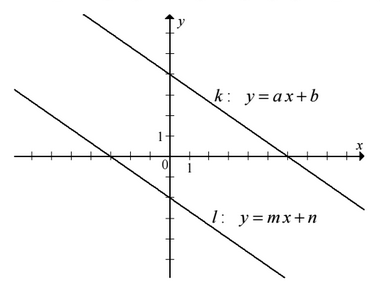
T/N : y=\frac{\sqrt{x}}{x-3} T/N : y=\frac{4}{2x-8}
T/N : y=-3x^2  
Zadanie 4.  1 pkt ⋅ Numer: pp-10893 ⋅ Poprawnie: 468/606 [77%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 Które z poniższych wzorów opisują funkcję malejącą?
Odpowiedzi:
T/N : y=\left(12-6\sqrt{3}\right)x+\sqrt{3} T/N : y=\left(11-6\sqrt{3}\right)x+2\sqrt{3}
T/N : y=\left(8-2\sqrt{13}\right)x+\sqrt{13}  
Zadanie 5.  1 pkt ⋅ Numer: pp-10891 ⋅ Poprawnie: 86/142 [60%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 « Wyznacz zbiór tych wartości parametru m, dla których funkcja liniowa f(x)=\frac{\left(36-m^2\right)}{4}x-9 jest rosnąca. Rozwiązanie zapisz w postaci sumy przedziałów.
Najmniejszy z końców liczbowych tych przedziałów jest równy p, a ilość liczb całkowitych należących do rozwiązania jest równa q.

Podaj liczby p i q.

Odpowiedzi:
p= (wpisz liczbę całkowitą)
q= (wpisz liczbę całkowitą)
Zadanie 6.  1 pkt ⋅ Numer: pp-10920 ⋅ Poprawnie: 99/154 [64%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 Funkcja określona wzorem f(x)=\left(m^2-2m\right)x+5 spełnia warunek f(-4)=f(4).

Wyznacz najmniejsze możliwe i największe możliwe m.

Odpowiedzi:
m_{min}= (wpisz liczbę całkowitą)
m_{max}= (wpisz liczbę całkowitą)
Zadanie 7.  1 pkt ⋅ Numer: pp-11532 ⋅ Poprawnie: 92/172 [53%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 (1 pkt) Funkcja liniowa określona wzorem f(x)=-3(m^2-5)x-4 jest malejąca, gdy:
Odpowiedzi:
A. m\in\left(-\sqrt{5},\sqrt{5}\right) B. m\in\left(-\infty, -\frac{\sqrt{15}}{5}\right)\cup\left(\frac{\sqrt{15}}{5}, +\infty\right)
C. m\in\left(-5,5\right) D. m\in\left(-\infty, -\sqrt{5}\right)\cup\left(\sqrt{5}, +\infty\right)
E. m\in\left(-\infty, -\frac{\sqrt{15}}{3}\right)\cup\left(\frac{\sqrt{15}}{3}, +\infty\right) F. m\in\left(-\infty, -5\right)\cup\left(5, +\infty\right)
Zadanie 8.  1 pkt ⋅ Numer: pp-10897 ⋅ Poprawnie: 62/104 [59%] Rozwiąż 
Podpunkt 8.1 (0.5 pkt)
 Wyznacz te wartości parametru m, dla których funkcja liniowa f(x)=(7-m^2)x+1 jest rosnąca. Rozwiązanie zapisz w postaci sumy przedziałów.
Liczba p jest najmniejszym z końców liczbowych tych przedziałów, a liczba q jest ilością liczb całkowitych należących do rozwiązania.

Podaj liczbę p.

Odpowiedź:
p= \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (0.5 pkt)
 Podaj liczbę q.
Odpowiedź:
q= (wpisz liczbę całkowitą)
Zadanie 9.  1 pkt ⋅ Numer: pp-10916 ⋅ Poprawnie: 130/224 [58%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Funkcja liniowa y=ax+b ma ujemne miejsce zerowe, a jej wykres przecina oś Oy poniżej punktu (0,0).

Wówczas:

Odpowiedzi:
A. a \lessdot 0 \wedge b > 0 B. a > 0 \wedge b \lessdot 0
C. a \lessdot 0 \wedge b \lessdot 0 D. a > 0 \wedge b > 0
Zadanie 10.  1 pkt ⋅ Numer: pp-10881 ⋅ Poprawnie: 194/250 [77%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 Wyznacz zbiór tych wszystkich wartości parametru m, dla których funkcja liniowa określona wzorem f(x)=\left(m^2-\frac{1}{16}\right)x+256 jest malejąca. Rozwiązanie zapisz w postaci sumy przedziałów.

Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (dwie liczby całkowite)
max= (dwie liczby całkowite)
Zadanie 11.  1 pkt ⋅ Numer: pp-10879 ⋅ Poprawnie: 123/207 [59%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 » Wyznacz zbiór tych wszystkich wartości parametru m, dla których funkcja liniowa określona wzorem f(x)=\left(m^2-36\right)x+2 jest rosnąca. Rozwiązanie zapisz w postaci sumy przedziałów.

Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (wpisz liczbę całkowitą)
max= (wpisz liczbę całkowitą)
Zadanie 12.  1 pkt ⋅ Numer: pp-10880 ⋅ Poprawnie: 121/206 [58%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 » Wyznacz zbiór tych wszystkich wartości parametru m, dla których funkcja liniowa określona wzorem f(x)=\left(4-m^2\right)x+2 jest malejąca. Rozwiązanie zapisz w postaci sumy przedziałów.

Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (wpisz liczbę całkowitą)
max= (wpisz liczbę całkowitą)
Zadanie 13.  1 pkt ⋅ Numer: pp-11504 ⋅ Poprawnie: 588/923 [63%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 (1 pkt) Funkcja f określona jest wzorem f(x)=(\sqrt{3}m+3)x+1 dla każdej liczby rzeczywistej x.

Funkcja ta jest rosnąca, wtedy i tylko wtedy, gdy:

Odpowiedzi:
A. m\in\left\langle \sqrt{3},+\infty\right) B. m\in\left(-\infty,\sqrt{3}\right\rangle
C. m\in\left\langle -\sqrt{3},+\infty\right) D. m\in\left(-\infty,-\sqrt{3}\right\rangle
Zadanie 14.  1 pkt ⋅ Numer: pp-10890 ⋅ Poprawnie: 66/116 [56%] Rozwiąż 
Podpunkt 14.1 (0.5 pkt)
 Wykres funkcji liniowej określonej wzorem h(x)=(\sqrt{6}-a)x+\frac{a}{2} jest prostą, która nie przechodzi tylko przez czwartą ćwiartkę układu współrzędnych.

Funkcja h spełnia ten warunek wtedy i tylko wtedy, gdy liczba a należy do pewnego przedziału o końcach p i q, przy czym p\lessdot q.

Podaj p.

Odpowiedź:
p= (wpisz liczbę całkowitą)
Podpunkt 14.2 (0.5 pkt)
 Podaj q.
Odpowiedź:
q= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 15.  1 pkt ⋅ Numer: pp-10892 ⋅ Poprawnie: 254/378 [67%] Rozwiąż 
Podpunkt 15.1 (0.8 pkt)
 Funkcja liniowa określona wzorem f(x)=6+4x-12mx jest malejąca, wtedy i tylko wtedy, gdy liczba m należy do pewnego przedziału.

Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
\frac{k}{n}=
(wpisz dwie liczby całkowite)
Podpunkt 15.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. -6 B. 2
C. -3 D. -2
E. +\infty F. -\infty
Zadanie 16.  1 pkt ⋅ Numer: pp-10902 ⋅ Poprawnie: 242/449 [53%] Rozwiąż 
Podpunkt 16.1 (0.8 pkt)
 Funkcja liniowa f(x)=(-4-m)x+2m jest malejąca, gdy parametr m należy do pewnego przedziału.

Podaj koniec tego przedziału, który jest liczbą całkowitą.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Podpunkt 16.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. -\frac{1}{2} B. \frac{1}{4}
C. \frac{1}{2} D. +\infty
E. -\infty F. -\frac{1}{4}
Zadanie 17.  1 pkt ⋅ Numer: pp-10903 ⋅ Poprawnie: 211/346 [60%] Rozwiąż 
Podpunkt 17.1 (0.8 pkt)
 Funkcja liniowa f(x)=(-8+3m)x+1-6m jest rosnąca, gdy parametr m należy do pewnego przedziału.

Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
\frac{k}{n}=
(wpisz dwie liczby całkowite)
Podpunkt 17.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. 10 B. -6
C. -\infty D. 7
E. 1 F. +\infty
Zadanie 18.  1 pkt ⋅ Numer: pp-10906 ⋅ Poprawnie: 54/153 [35%] Rozwiąż 
Podpunkt 18.1 (0.8 pkt)
 Wykres funkcji liniowej f(x)=-5x-5a przecina oś Oy poniżej punktu (0,8) wtedy i tylko wtedy, gdy parametr a należy do pewnego przedziału.

Podaj ten z końców tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
Wpisz odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 18.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. -\infty B. +\infty
C. 6 D. 0
E. -4 F. -3
Zadanie 19.  1 pkt ⋅ Numer: pp-10907 ⋅ Poprawnie: 147/265 [55%] Rozwiąż 
Podpunkt 19.1 (0.8 pkt)
 Wykres funkcji liniowej f(x)=2x-5a przecina oś Oy powyżej punktu (0,8) wtedy i tylko wtedy, gdy parametr a należy do pewnego przedziału.

Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
Wpisz odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 19.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. -\infty B. -4
C. 0 D. +\infty
E. -3 F. 6
Zadanie 20.  1 pkt ⋅ Numer: pp-10912 ⋅ Poprawnie: 117/194 [60%] Rozwiąż 
Podpunkt 20.1 (0.8 pkt)
 Wyznacz przedział tych wszystkich wartości m, dla których funkcja f(x)=\left(-2m+\frac{8}{3}\right)x-m jest rosnąca.

Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
\frac{k}{n}=
(wpisz dwie liczby całkowite)
Podpunkt 20.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. +\infty B. 1
C. 7 D. 10
E. -\infty F. -6
Zadanie 21.  1 pkt ⋅ Numer: pp-10913 ⋅ Poprawnie: 77/140 [55%] Rozwiąż 
Podpunkt 21.1 (0.8 pkt)
 Wyznacz przedział tych wszystkich wartości m, dla których funkcja liniowa f(x)=\left(-\frac{5}{2}m+4\right)x-m jest rosnąca.

Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
\frac{k}{n}=
(wpisz dwie liczby całkowite)
Podpunkt 21.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. +\infty B. -\infty
C. -8 D. 1
E. 0 F. -12
Zadanie 22.  1 pkt ⋅ Numer: pp-10917 ⋅ Poprawnie: 97/189 [51%] Rozwiąż 
Podpunkt 22.1 (1 pkt)
 » Funkcja liniowa określona wzorem f(x)=ax+b jest rosnąca i ma miejsce zerowe \frac{\sqrt{80}-9}{2}.

Wynika z tego, że:

Odpowiedzi:
A. a \lessdot 0 \wedge b > 0 B. a > 0 \wedge b > 0
C. a \lessdot 0 \wedge b < 0 D. a > 0 \wedge b \lessdot 0
Zadanie 23.  1 pkt ⋅ Numer: pp-10918 ⋅ Poprawnie: 83/138 [60%] Rozwiąż 
Podpunkt 23.1 (1 pkt)
 « Funkcja liniowa określona wzorem f(x)=ax+b jest malejąca i ma miejsce zerowe \frac{\sqrt{27}-5}{2}.

Wynika z tego, że:

Odpowiedzi:
A. a > 0 \wedge b > 0 B. a > 0 \wedge b \lessdot 0
C. a \lessdot 0 \wedge b < 0 D. a \lessdot 0 \wedge b > 0
Zadanie 24.  1 pkt ⋅ Numer: pp-10749 ⋅ Poprawnie: 137/162 [84%] Rozwiąż 
Podpunkt 24.1 (1 pkt)
 Funkcja f opisana jest wzorem: f(x)=\frac{3}{8}x+3. Jeśli argument funkcji f wzrośnie o 5, to wartość tej funkcji:
Odpowiedzi:
A. wzrośnie o \frac{3}{2} B. wzrośnie o \frac{9}{4}
C. zmaleje o \frac{15}{8} D. wzrośnie o \frac{15}{8}
Zadanie 25.  1 pkt ⋅ Numer: pp-10882 ⋅ Poprawnie: 218/416 [52%] Rozwiąż 
Podpunkt 25.1 (0.8 pkt)
 Funkcja liniowa określona wzorem f(x)=\left(-\frac{5}{6}+5m\right)x+5 jest rosnąca, gdy m należy do pewnego przedziału.

Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.

Odpowiedź:
\frac{k}{n}=
(wpisz dwie liczby całkowite)
Podpunkt 25.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. 7 B. +\infty
C. 1 D. -12
E. -\infty F. 10
Zadanie 26.  1 pkt ⋅ Numer: pp-10919 ⋅ Poprawnie: 219/321 [68%] Rozwiąż 
Podpunkt 26.1 (1 pkt)
 Funkcja f jest liniowa oraz f(-4)=-3 i f(-3)=1.

Oblicz f(0).

Odpowiedź:
f(0)= (wpisz liczbę całkowitą)
Zadanie 27.  1 pkt ⋅ Numer: pp-10924 ⋅ Poprawnie: 60/80 [75%] Rozwiąż 
Podpunkt 27.1 (1 pkt)
 Funkcja liniowa f określona jest wzorem f(x)=ax+b i spełnia warunek f(7)-f(4)=18.

Wyznacz a.

Odpowiedź:
a= (wpisz liczbę całkowitą)
Zadanie 28.  1 pkt ⋅ Numer: pp-10910 ⋅ Poprawnie: 407/672 [60%] Rozwiąż 
Podpunkt 28.1 (1 pkt)
 Do wykresu funkcji liniowej y=ax+b należą punkty (-2, 0) i (0, 1).

Oceń prawdziwość poniższych koniunkcji:
(znak \wedge oznacza spójnik "i")

Odpowiedzi:
T/N : a \lessdot 0 \wedge b < 0 T/N : a > 0 \wedge b \lessdot 0
T/N : a \lessdot 0 \wedge b > 0  
Zadanie 29.  1 pkt ⋅ Numer: pp-10898 ⋅ Poprawnie: 71/119 [59%] Rozwiąż 
Podpunkt 29.1 (1 pkt)
 Wykres funkcji liniowej y=2^{16}x+2^{21} przechodzi przez ćwiartki układu współrzędnych:
Odpowiedzi:
A. I, III i IV B. II, III, IV
C. I, II i IV D. I, II i III
Zadanie 30.  1 pkt ⋅ Numer: pp-10877 ⋅ Poprawnie: 137/250 [54%] Rozwiąż 
Podpunkt 30.1 (1 pkt)
 » Dana jest funkcja f(x)=ax+b. Warunek f(x) \lessdot 0 spełnia każde x dodatnie, a warunek f(x) > 0 spełnia każde x ujemne.

Wynika z tego, że:

Odpowiedzi:
A. a=0 \wedge b \lessdot 0 B. a \lessdot 0 \wedge b=0
C. a > 0 D. a=0
Zadanie 31.  1 pkt ⋅ Numer: pp-10901 ⋅ Poprawnie: 80/141 [56%] Rozwiąż 
Podpunkt 31.1 (1 pkt)
 Proporcjonalnością prostą jest zależność opisana wzorem:
Odpowiedzi:
A. y=\frac{\sqrt{2}x}{2} B. y=\frac{2}{\sqrt{2}x}
C. y=4x^2 D. y=\frac{4}{x}
Zadanie 32.  1 pkt ⋅ Numer: pp-10884 ⋅ Poprawnie: 141/181 [77%] Rozwiąż 
Podpunkt 32.1 (1 pkt)
 Funkcja liniowa f określona jest wzorem f(x)=2^{16}x+2^{21}.

Prosta będąca wykresem funkcji f nie przechodzi przez ćwiartkę układu:

Odpowiedzi:
A. pierwszą B. drugą
C. czwartą D. trzecią
Zadanie 33.  1 pkt ⋅ Numer: pp-10885 ⋅ Poprawnie: 112/182 [61%] Rozwiąż 
Podpunkt 33.1 (1 pkt)
 Wykres funkcji liniowej f określonej wzorem f(x)=ax+b nie przechodzi tylko przez ćwiartkę układu współrzędnych o numerze 2.

Wówczas:

Odpowiedzi:
A. a\lessdot 0 \wedge b<0 B. a>0 \wedge b\lessdot 0
C. a>0 \wedge b>0 D. a\lessdot 0 \wedge b>0
Zadanie 34.  1 pkt ⋅ Numer: pp-10921 ⋅ Poprawnie: 203/356 [57%] Rozwiąż 
Podpunkt 34.1 (1 pkt)
 » Wykresy funkcji f(x)=-3x-mx-3 i y=x+7 nie mają punktów wspólnych.

Wyznacz m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 35.  1 pkt ⋅ Numer: pp-10878 ⋅ Poprawnie: 216/407 [53%] Rozwiąż 
Podpunkt 35.1 (0.8 pkt)
 Funkcja określona wzorem f(x)=\left(-\frac{3}{7}-\frac{\sqrt{3}}{2}m\right)x+2 jest rosnąca, gdy parametr m należy do pewnego przedziału.

Podaj koniec tego przedziału, który jest liczbą niewymierną.

Odpowiedź:
\frac{k\sqrt{n}}{p}= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 35.2 (0.2 pkt)
 Drugim końcem tego przedziału jest:
Odpowiedzi:
A. -\infty B. \frac{2}{21}
C. -\frac{4}{7} D. +\infty
E. -\frac{2}{21} F. \frac{3}{7}
Zadanie 36.  1 pkt ⋅ Numer: pp-10883 ⋅ Poprawnie: 123/271 [45%] Rozwiąż 
Podpunkt 36.1 (1 pkt)
« Proste p i q są równoległe, a punkt O(0,0) leży pomiędzy nimi.

Zatem:

Odpowiedzi:
A. a\cdot m \lessdot 0 \ \wedge\ b\cdot n > 0 B. a\cdot m \lessdot 0 \ \wedge\ b\cdot n < 0
C. a\cdot m > 0 \ \wedge\ b\cdot n \lessdot 0 D. a\cdot m > 0 \ \wedge\ b\cdot n > 0
Zadanie 37.  1 pkt ⋅ Numer: pp-10887 ⋅ Poprawnie: 214/297 [72%] Rozwiąż 
Podpunkt 37.1 (1 pkt)
 Wykresy funkcji liniowych opisanych wzorami f(x)=3x+\frac{5}{4} i g(x)=6 opisują proste:
Odpowiedzi:
A. pokrywające się B. równoległe i różne
C. przecinające się pod kątem o mierze 90^{\circ} D. przecinające się pod kątem różnym od 90^{\circ}
Zadanie 38.  1 pkt ⋅ Numer: pp-10908 ⋅ Poprawnie: 101/147 [68%] Rozwiąż 
Podpunkt 38.1 (1 pkt)
 Funkcja liniowa f(x)=(2-m)x+(m+1)^2-5 jest rosnąca i jej wykres przecina oś rzędnych w punkcie P=(0,44).

Wyznacz m.

Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 39.  1 pkt ⋅ Numer: pp-10909 ⋅ Poprawnie: 99/226 [43%] Rozwiąż 
Podpunkt 39.1 (1 pkt)
 Wskaż prostą prostopadłą do osi Ox:
Odpowiedzi:
A. -5y+4=0 B. 4y=x
C. 4y=0 D. x-4=y
E. -4x+y=0 F. -5x+4=0
Zadanie 40.  1 pkt ⋅ Numer: pp-10911 ⋅ Poprawnie: 198/317 [62%] Rozwiąż 
Podpunkt 40.1 (1 pkt)
 Wskaż prostą równoległą do osi Ox:
Odpowiedzi:
A. -5x+4=0 B. x-4=y
C. 4x=-5y D. 4x=-5
E. -5y+4=0 F. 4x=0
Zadanie 41.  1 pkt ⋅ Numer: pp-10889 ⋅ Poprawnie: 39/63 [61%] Rozwiąż 
Podpunkt 41.1 (1 pkt)
 Dla której z podanych wartości m funkcja liniowa określona wzorem f(x)=-25x+m^2-9+m^4 x jest malejąca:
Odpowiedzi:
A. m=\sqrt{5}+1 B. m=5
C. m=-\frac{\sqrt{5}}{5} D. m=-2\sqrt{5}
Zadanie 42.  1 pkt ⋅ Numer: pp-11765 ⋅ Poprawnie: 674/975 [69%] Rozwiąż 
Podpunkt 42.1 (1 pkt)
 Wykres funkcji liniowej określonej wzorem f(x)=ax+b, przechodzi przez pierwszą, drugą i czwartą ćwiartkę układu współrzędnych.

Wówczas liczby a i b spełniają warunki:

Odpowiedzi:
A. a\lessdot 0 \wedge b \lessdot 0 B. a > 0 \wedge b \lessdot 0
C. a > 0 \wedge b > 0 D. a\lessdot 0 \wedge b > 0
Zadanie 43.  1 pkt ⋅ Numer: pp-11785 ⋅ Poprawnie: 671/868 [77%] Rozwiąż 
Podpunkt 43.1 (1 pkt)
 Wykresy funkcji liniowych f(x)=(-m+1)x-4 oraz g(x)=-x nie mają punktów wspólnych dla:
Odpowiedzi:
A. m=3 B. m=2
C. m=0 D. m=6
E. m=1 F. m=4
Zadanie 44.  1 pkt ⋅ Numer: pp-11914 ⋅ Poprawnie: 200/273 [73%] Rozwiąż 
Podpunkt 44.1 (1 pkt)
 Funkcja liniowa f określona wzorem f(x)=(3m+1)x+22 jest rosnąca dla:
Odpowiedzi:
A. m >-\frac{1}{12} B. m >-\frac{1}{3}
C. m \lessdot -\frac{5}{12} D. m >-\frac{2}{9}
E. m \lessdot \frac{2}{3} F. m >\frac{4}{3}
Zadanie 45.  1 pkt ⋅ Numer: pp-11950 ⋅ Poprawnie: 51/73 [69%] Rozwiąż 
Podpunkt 45.1 (1 pkt)
 Na płaszczyźnie, w kartezjańskim układzie współrzędnych (x, y), dane są:
  • prosta k o równaniu y=-3x+1,
  • prosta l o równaniu y+9=\frac{1}{3}x.

Proste k i l:

Odpowiedzi:
A. są prostopadłe B. przecinają się pod kątem 30^{\circ}
C. nie mają punktów wspólnych D. się pokrywają
Zadanie 46.  1 pkt ⋅ Numer: pp-11988 ⋅ Poprawnie: 580/827 [70%] Rozwiąż 
Podpunkt 46.1 (1 pkt)
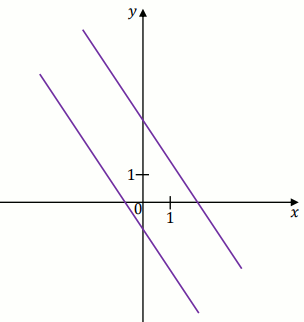
 Na rysunku, w kartezjańskim układzie współrzędnych (x, y), przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań A–D.

Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest:

Odpowiedzi:
A. \begin{cases}y=-\frac{5}{6}x+7\\y=\frac{6}{5}x+5\end{cases} B. \begin{cases}y=\frac{5}{6}x+7\\y=\frac{5}{6}x-5\end{cases}
C. \begin{cases}y=-\frac{5}{6}x+7\\y=-\frac{5}{6}x+5\end{cases} D. \begin{cases}y=-\frac{5}{6}x+7\\y=-\frac{5}{6}x-5\end{cases}
Zadanie 47.  1 pkt ⋅ Numer: pp-11989 ⋅ Poprawnie: 523/743 [70%] Rozwiąż 
Podpunkt 47.1 (1 pkt)
 Funkcja liniowa f jest określona wzorem f(x)=(-3k+1)x+k-4, gdzie k\in\mathbb{R}.

Funkcja f jest malejąca dla każdej liczby k należącej do przedziału:

Odpowiedzi:
A. \left(\frac{1}{6},+\infty\right) B. \left(-\frac{1}{3},+\infty\right)
C. \left(\frac{1}{3},+\infty\right) D. \left(\frac{1}{2},+\infty\right)
E. \left(-\infty,\frac{2}{9}\right) F. \left(-\infty,-\frac{1}{2}\right)
Zadanie 48.  1 pkt ⋅ Numer: pp-12060 ⋅ Poprawnie: 122/128 [95%] Rozwiąż 
Podpunkt 48.1 (1 pkt)
 Proste o równaniach y=3x-5 oraz y=\frac{m-3}{2}x+1 są równoległe, gdy m jest równe:
Odpowiedzi:
A. 6 B. 14
C. 9 D. 15
E. 11 F. 12
G. 3 H. 7
Zadanie 49.  1 pkt ⋅ Numer: pp-12370 ⋅ Poprawnie: 160/185 [86%] Rozwiąż 
Podpunkt 49.1 (1 pkt)
 Miejscem zerowym funkcji liniowej f określonej wzorem f(x)=ax+b jest liczba 2, a punkt przecięcia wykresu funkcji f z osią Ox kartezjańskiego układu współrzędnych (x, y) ma współrzędne (0,4) (zobacz rysunek).

Oceń poprawność poniższych zdań:

Odpowiedzi:
T/N : a\cdot b > 0 T/N : prosta odcina na osiach układu trójkąt o polu równym 8
Zadanie 50.  2 pkt ⋅ Numer: pp-20333 ⋅ Poprawnie: 110/291 [37%] Rozwiąż 
Podpunkt 50.1 (1 pkt)
 « Wykres funkcji rosnącej g(x)=(4m+1)x+2m-3 nie przechodzi przez drugą ćwiartkę układu współrzędnych. Wyznacz zbiór wszystkich możliwych wartości parametru m\in\mathbb{R}.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z tych wszystkich z konców liczbowych tych przedziałów.

Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 50.2 (1 pkt)
 Podaj największy z wszystkich konców liczbowych tych przedziałów.
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 51.  2 pkt ⋅ Numer: pp-20334 ⋅ Poprawnie: 32/133 [24%] Rozwiąż 
Podpunkt 51.1 (2 pkt)
 «« Zbadaj monotoniczność funkcji f(x)=(4-\sqrt{5}m)x+2 dla m=\frac{15}{2}\sqrt{5}-1.

O ile rośnie lub maleje wartość tej funkcji jeśli argument rośnie o 1?

Odpowiedź:
\frac{a+b\sqrt{c}}{d}= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 52.  2 pkt ⋅ Numer: pp-21122 ⋅ Poprawnie: 50/62 [80%] Rozwiąż 
Podpunkt 52.1 (2 pkt)
 Funkcja liniowa f przyjmuje wartość -6 dla argumentu 0, a ponadto f(8)-f(6)=20. Wyznacz wzór funkcji f(a)=ax+b.

Podaj wartości współczynników a i b.

Odpowiedzi:
a= (wpisz liczbę całkowitą)
b= (wpisz liczbę całkowitą)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm