⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Układy równań pierwszego stopnia z dwiema niewiadomymi- metoda podstawiania
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- równania liniowe
- układy równań stopnia pierwszego z dwiema niewiadomymi
- zastosowania układów równań
| Zadanie 1. 1 pkt ⋅ Numer: pp-10872 ⋅ Poprawnie: 386/506 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Którą parę prostych pokazano na rysunku:
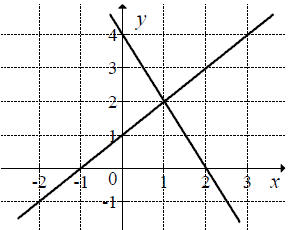
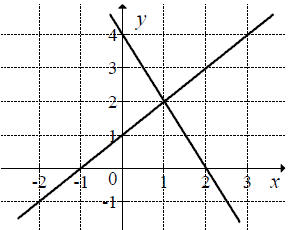
Odpowiedzi:
| A. y=x+1\wedge y=2x+4 | B. y=x-1\wedge y=2x+4 |
| C. y=x+1\wedge y=-2x+4 | D. y=x-1\wedge y=-2x+4 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10863 ⋅ Poprawnie: 297/475 [62%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Układ równań
\begin{cases}
8x+8y=4 \\
5y+5x=-4
\end{cases}
:
Odpowiedzi:
| A. jest oznaczony | B. jest nieoznaczony |
| C. ma dwa rozwiązania | D. jest sprzeczny |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10874 ⋅ Poprawnie: 744/886 [83%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Rozwiązaniem układu równań
\begin{cases}
2x+7y=\frac{11}{2} \\
2x-7y=-\frac{3}{2}
\end{cases}
jest para liczb:
Odpowiedzi:
| A. x=2\wedge y=\frac{1}{2} | B. x=0\wedge y=1 |
| C. x=1\wedge y=\frac{1}{2} | D. x=1\wedge y=\frac{3}{2} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10862 ⋅ Poprawnie: 327/420 [77%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Interpretacją geometryczną układu równań
\begin{cases}
3y+3x=-1 \\
y-1=0
\end{cases}
są dwie proste przecinające się w ćwiartce układu współrzędnych:
Odpowiedzi:
| A. trzeciej | B. pierwszej |
| C. czwartej | D. drugiej |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10850 ⋅ Poprawnie: 118/218 [54%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Układ równań
\begin{cases}
y=-2(a+3)x-2b-6 \\
y=\frac{4}{b+3}x+a+3
\end{cases}
ma nieskończenie wiele rozwiązań dla:
Odpowiedzi:
| A. a=-5 \wedge b=-1 | B. a=-7 \wedge b=-1 |
| C. a=-5 \wedge b=-2 | D. a=-4 \wedge b=-2 |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10851 ⋅ Poprawnie: 158/250 [63%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Wskaż parę prostych widocznych na rysunku:
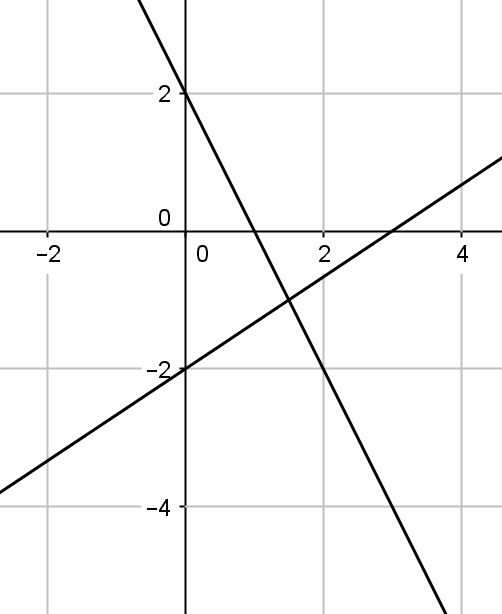
Odpowiedzi:
| A. y=-2x-2\wedge y=\frac{3}{2}x+2 | B. y=-2x+2\wedge y=\frac{2}{3}x-2 |
| C. y=-2x-2\wedge y=\frac{2}{3}x+2 | D. y=-2x+2\wedge y=\frac{3}{2}x-2 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10865 ⋅ Poprawnie: 289/439 [65%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
» Układ równań
\begin{cases}
8x+8y=4 \\
5y=-4-5x
\end{cases}
:
Odpowiedzi:
| A. jest oznaczony | B. jest sprzeczny |
| C. ma dwa rozwiązania | D. jest nieoznaczony |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11834 ⋅ Poprawnie: 847/806 [105%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Dany jest układ równań
\begin{cases}
x-3y+9=0\\
2x+y-3=0
\end{cases}.
Rozwiązaniem tego układu równań jest para liczb:
Odpowiedzi:
| A. x=-1 \wedge y=5 | B. x=1 \wedge y=2 |
| C. x=0 \wedge y=3 | D. x=1 \wedge y=4 |
| E. x=2 \wedge y=2 | F. x=-1 \wedge y=2 |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11942 ⋅ Poprawnie: 177/175 [101%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Klient banku wypłacił z bankomatu kwotę 5970 zł. Bankomat wydał kwotę
w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100-złotowych było 4 razy więcej
niż 50-złotowych, a banknotów 20-złotowych było o 7 mniej niż 50-złotowych.
Niech x oznacza liczbę banknotów 50-złotowych, a y – liczbę banknotów
20-złotowych, które otrzymał ten klient.
Poprawny układ równań prowadzący do obliczenia liczb x i y to:
Odpowiedzi:
| A. \begin{cases}50x+50x\cdot 4+20y=5970\\y=x-7\end{cases} | B. \begin{cases}50x+100\cdot 4x+20y=5970\\x=y-7\end{cases} |
| C. \begin{cases}50x+50x\cdot 4x+20y=5970\\y=x-7\end{cases} | D. \begin{cases}50x+50x\cdot 4+20y=5970\\y=x+7\end{cases} |
| E. \begin{cases}50x+100x\cdot 4x+20y=5970\\y=x-7\end{cases} | F. \begin{cases}50x+100\cdot 4x+20y=5970\\y=x-7\end{cases} |
| Zadanie 10. 1 pkt ⋅ Numer: pp-11964 ⋅ Poprawnie: 150/147 [102%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Dany jest układ równań
\begin{cases}y=-x-1\\y=x-1\end{cases}.
Na którym z rysunków przedstawiona jest interpretacja geometryczna tego układu równań?
Odpowiedzi:
A.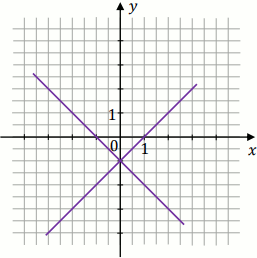 
|
B.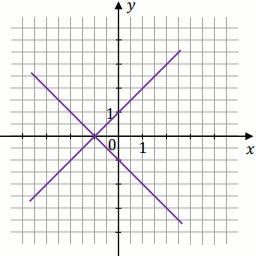 
|
C.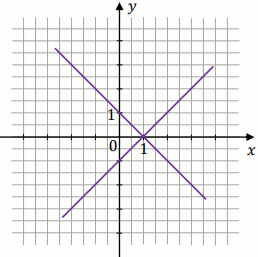 
|
D.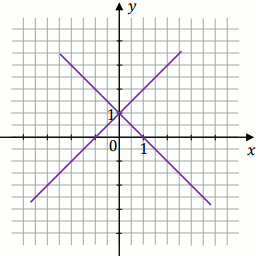 
|
| Zadanie 11. 1 pkt ⋅ Numer: pp-12028 ⋅ Poprawnie: 247/153 [161%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Para liczb x=1, y=-3 spełnia układ równań
\begin{cases}x-y=(a+3)^2\\(4+a)x-3y=-4(a+3)\end{cases}.
Wtedy a jest równe:
Odpowiedzi:
| A. -3-\sqrt{2}} | B. -\frac{5}{2} |
| C. -5 | D. 5 |
| E. -\frac{9}{2} | F. -3+\sqrt{2}} |
| Zadanie 12. 1 pkt ⋅ Numer: pp-12059 ⋅ Poprawnie: 198/144 [137%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów
równań.
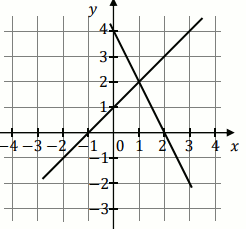
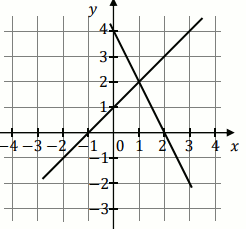
Wskaż ten układ, którego geometryczną interpretację przedstawiono na rysunku:
Odpowiedzi:
| A. \begin{cases}y=x-1\\y=-2x-4\end{cases} | B. \begin{cases}y=x-1\\y=2x+4\end{cases} |
| C. \begin{cases}y=x+1\\y=2x+4\end{cases} | D. \begin{cases}y=x+1\\y=2x-4\end{cases} |
| E. \begin{cases}y=x+1\\y=-2x+4\end{cases} | F. \begin{cases}y=x-1\\y=-2x+4\end{cases} |
| Zadanie 13. 1 pkt ⋅ Numer: pp-12369 ⋅ Poprawnie: 230/237 [97%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Para liczb x=-5 i y=4 jest rozwiązaniem
układu równań \begin{cases}ax+3y=-3\\x+by=-1\end{cases},
gdzie a oraz b są liczbami rzeczywistymi.
Wartość wyrażenia a\cdot b jest równa:
Odpowiedzi:
| A. 3 | B. 39 |
| C. -14 | D. 26 |
| E. 42 | F. 32 |
| Zadanie 14. 2 pkt ⋅ Numer: pp-20325 ⋅ Poprawnie: 166/381 [43%] | Rozwiąż |
Podpunkt 14.1 (2 pkt)
» Rozwiąż układ równań
\begin{cases}
3x+2y=3 \\
y+2=\frac{3(1-x)+4}{2}
\end{cases}
.
Punkt A=(4, m) należy do rozwiązania. Podaj m.
Odpowiedź:
| \frac{p}{q}= | |