⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Twierdzenie Talesa
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- twierdzenie Talsesa
- równoległe w trójkącie
- stosunki odcinków równoległych
- wzory Talesa
- twierdzenie odwrotne od twierdzenia Talesa
| Zadanie 1. 1 pkt ⋅ Numer: pp-11383 ⋅ Poprawnie: 671/870 [77%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Odcinek AB o długości 30 jest
równoległy do odcinka CD, przy czym:
|PA|=12 i
|AC|=20:
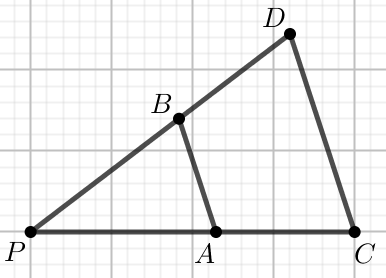
Oblicz długość odcinka CD.
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10601 ⋅ Poprawnie: 674/896 [75%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Odcinki BC i EF
na rysunku są równoległe, przy czym
|AC|=\frac{11}{2} i
|BC|=18:
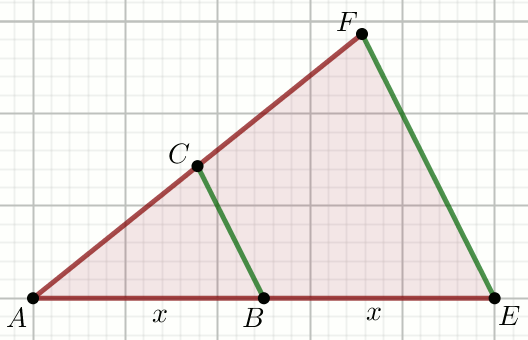
Oblicz długość odcinka EF.
Odpowiedź:
|EF|=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10602 ⋅ Poprawnie: 503/737 [68%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Zielone odcinki na rysunku sa równolegle, przy czym
|AP|=\frac{2}{3},
|BP|=\frac{5}{6},
|CP|=\frac{5}{3},
|DP|=\frac{4}{3},
|AB|=\frac{5}{3}:
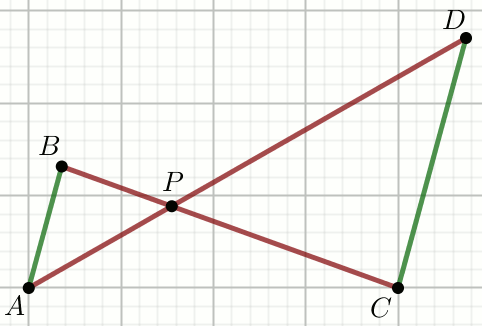
Oblicz długość odcinka CD.
Odpowiedź:
| |CD|= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10603 ⋅ Poprawnie: 229/386 [59%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{2}{3},
|DC|=\frac{5}{6} i
|AB|=\frac{5}{6}:
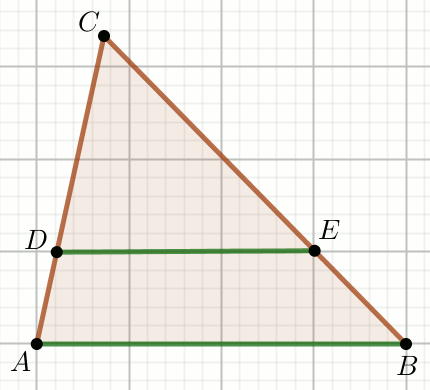
Oblicz długość odcinka DE.
Odpowiedź:
| |DE|= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10604 ⋅ Poprawnie: 189/266 [71%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{2}{3},
|DC|=\frac{5}{6} i
|DE|=\frac{5}{6}:
Oblicz długość odcinka AB.
Odpowiedź:
| |AB|= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10605 ⋅ Poprawnie: 170/279 [60%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{1}{4},
|DE|=\frac{1}{6} i
|AB|=\frac{3}{4}:
Oblicz długość odcinka DC.
Odpowiedź:
| |DC|= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10594 ⋅ Poprawnie: 146/237 [61%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
W trójkącie ABC poprowadzono odcinek
DE równoległy do boku AB, przy czym
|AB|=\frac{9}{2} i
|BE|:|EC|=6:
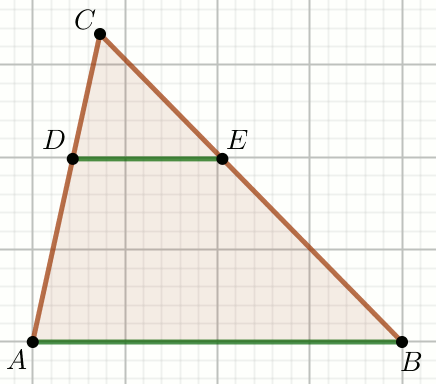
Oblicz długość odcinka DE.
Odpowiedź:
| |DE|= | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10600 ⋅ Poprawnie: 369/516 [71%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Odcinki DE i AB są
równoległe, przy czym
|CD|=\frac{5}{4} i
|CE|=1:
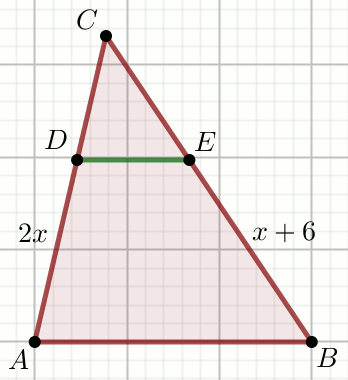
Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10596 ⋅ Poprawnie: 221/354 [62%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
« Odcinki DE i AB
są równoległe, przy czym
|DE|=\frac{1}{6} i
|AB|=1:
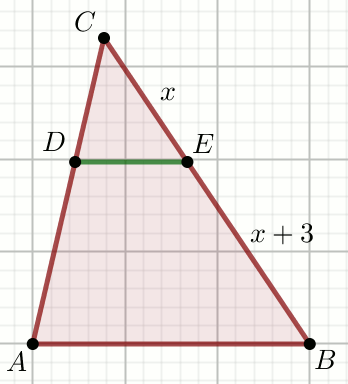
Oblicz x.
Odpowiedź:
| x= | |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10595 ⋅ Poprawnie: 274/427 [64%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AP|=1,
|BP|=\frac{5}{4} i
|CP|=\frac{10}{3}:
Oblicz długość odcinka DP.
Odpowiedź:
| |DP|= | |
| Zadanie 11. 2 pkt ⋅ Numer: pp-20250 ⋅ Poprawnie: 131/248 [52%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
» W trapezie ABCD,
AB\parallel CD oraz dane są długości trzech odcinków:
|AB|=18, CD=\frac{35}{2} i
|AD|=7:
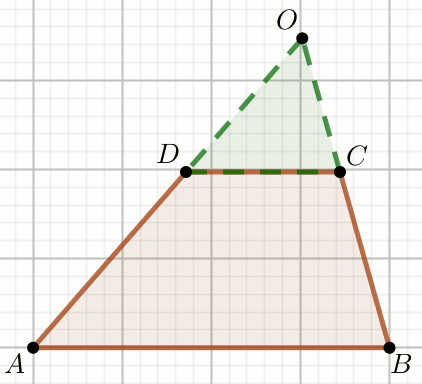
O ile należy wydłużyć ramię AD, aby przecięło się z przedłużeniem ramienia BC:
Odpowiedź:
| d= | |
| Zadanie 12. 2 pkt ⋅ Numer: pp-20251 ⋅ Poprawnie: 94/262 [35%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=\frac{25}{4},
|AB|=10,
|AD|=5 i
|BC|=\frac{15}{4}.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 13. 3 pkt ⋅ Numer: pp-20252 ⋅ Poprawnie: 119/350 [34%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
W trójkącie ABC odcinek EF
jest symetralną boku AB oraz
|AD|=3,
|DB|=77 i
|BC|=85:
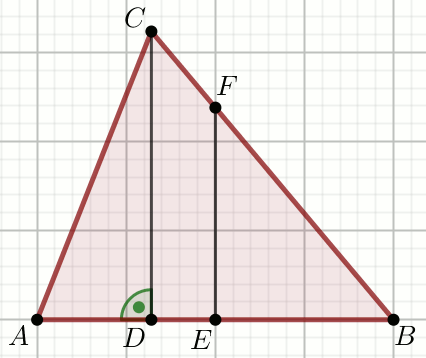
Wyznacz długości odcinków CF i FB. Podaj długość krótszego z tych odcinków.
Odpowiedź:
| min= | |
Podpunkt 13.2 (2 pkt)
Podaj długość dłuższego z tych odcinków.
Odpowiedź:
| max= | |
| Zadanie 14. 2 pkt ⋅ Numer: pp-20863 ⋅ Poprawnie: 40/169 [23%] | Rozwiąż |
Podpunkt 14.1 (2 pkt)
(2 pkt)
W trójkącie równoramiennym ABC dane są długości boków:
|AC|=|BC|=70 i |AB|=84.
Na przedłużeniu boku AB zaznaczono taki punkt D,
że |DB|=147. Przez punkt A
poprowadzono prostą równoległą do boku BC, która przecięła odcinek
DC w punkcie E (zobacz rysunek):
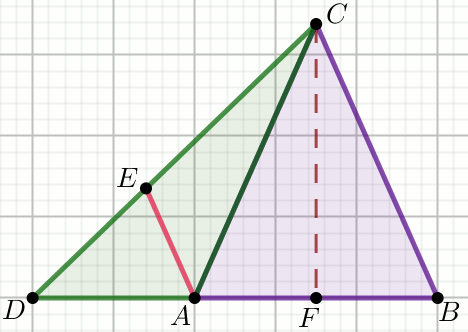
Oblicz |DE|.
Odpowiedź:
| |DE|= | |
| Zadanie 15. 2 pkt ⋅ Numer: pp-20878 ⋅ Poprawnie: 34/51 [66%] | Rozwiąż |
Podpunkt 15.1 (2 pkt)
W trójkącie ABC poprowadzono trzy proste równoległe do podstawy
AB, które podzieliły bok BC na cztery
odcinki równej długości.
Suma długości odcinków tych prostych zawartych wewnątrz tego trójkąta jest o
26 większa od długości jego podstawy AB.
Oblicz |AB|.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)