Twierdzenie Pitagorasa
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- twierdzenie Pitagorasa
- twierdzenie odwrotne
- trójkąt prostokątny
- badanie ostrokątności trójkąta
| Zadanie 1. 1 pkt ⋅ Numer: pp-11463 ⋅ Poprawnie: 173/256 [67%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Dwa boki trójkąta maja długość 14 i
29. Trzeci bok tego trójkąta należy do przedziału
(a,b).
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11462 ⋅ Poprawnie: 195/348 [56%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Trójkąt o bokach długości \sqrt{2}+1,
\sqrt{2}+1, 2+\sqrt{2}, jest:
Odpowiedzi:
| A. nie istnieje | B. jest rozwartokątny |
| C. jest ostrokątny | D. jest prostokątny |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10583 ⋅ Poprawnie: 281/376 [74%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Trójkąt równoramienny prostokątny ma przeciwprostokątną długości
6+8\sqrt{2}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 4. 1 pkt ⋅ Numer: pp-11560 ⋅ Poprawnie: 51/76 [67%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 2+2\sqrt{2}, -2+2\sqrt{2}, 4\sqrt{2} | T/N : 4, 2, 2\sqrt{5} |
| T/N : 2\sqrt{10}, 2\sqrt{6}, 2\sqrt{5} |
| Zadanie 5. 1 pkt ⋅ Numer: pp-12071 ⋅ Poprawnie: 47/76 [61%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
W trójkącie ABC bok BC ma długość
45, a wysokość CD tego trójkąta
dzieli bok AB na odcinki o długościach
|AD|=3 i |BD|=36 (zobacz rysunek).
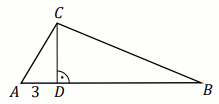

Długość boku AC jest równa:
Odpowiedzi:
| A. \frac{369}{2} | B. 3\sqrt{82} |
| C. \frac{3\sqrt{82}}{2} | D. 4\sqrt{82} |
| E. \frac{9\sqrt{82}}{8} | F. \sqrt{82} |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20712 ⋅ Poprawnie: 62/136 [45%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Punkt O jest środkiem okręgu na rysunku, przy czym
x=44 i
y=\frac{57}{4}:
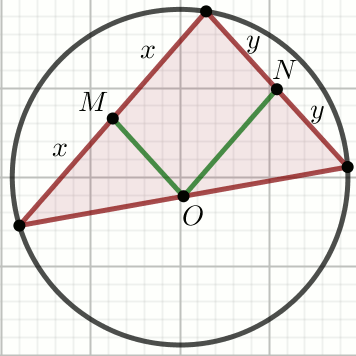

Długość tego okręgu jest równa p\cdot \pi.
Podaj liczbę p.
Odpowiedź:
| p= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20713 ⋅ Poprawnie: 367/726 [50%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Długości dwóch najkrótszych boków trójkąta prostokątnego pozostają w stosunku
4:3, a obwód tego trójkąta ma długość
72.
Wyznacz długość najkrótszego boku tego trójkąta.
Odpowiedź:
| min= | |
Podpunkt 7.2 (1 pkt)
Wyznacz długość najdłuższego boku tego trójkąta.
Odpowiedź:
| max= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20714 ⋅ Poprawnie: 93/160 [58%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Czworokąt na rysunku jest prostokątem, w którym
|DP|:|PC|=\frac{1}{5}:
Oceń, czy kąt
\alpha jest prosty, ostry czy rozwarty:
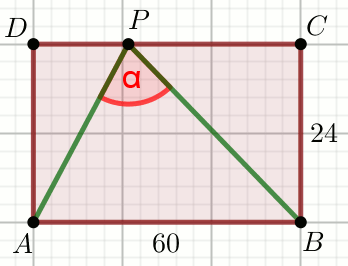

Jeśli kąt \alpha jest prosty wpisz 0, jeśli ostry wpisz 1, jeśli rozwarty wpisz 2.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20241 ⋅ Poprawnie: 231/405 [57%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
W trójkącie równoramiennym
AC oraz BC są ramionami oraz.
|AC|=5,
|BC|=5 i
|AB|=2\sqrt{14}:
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
P_{\triangle}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20243 ⋅ Poprawnie: 98/237 [41%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
» Boki trójkąta prostokątnego mają długości: a,
6 i 12.
Podaj najmniejszą możliwą wartość a.
Odpowiedź:
a_{min}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 10.2 (1 pkt)
Podaj największą możliwą wartość a.
Odpowiedź:
a_{max}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 11. 2 pkt ⋅ Numer: pp-20875 ⋅ Poprawnie: 65/108 [60%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« W trójkącie prostokątnym najkrótszy bok ma długość 10, a
najdłuższy bok jest dłuższy od dłuższej przyprostokątnej o 2.
Oblicz długość dłuższej przyprostokątnej tego trójkąta.
Odpowiedź:
| max= | |
Podpunkt 11.2 (1 pkt)
Oblicz obwód tego trójkąta.
Odpowiedź:
| L= | |
| Zadanie 12. 2 pkt ⋅ Numer: pp-20873 ⋅ Poprawnie: 42/59 [71%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
Obwód trójkąta prostokątnego ma długość 30, a
stosunek długość przyprostokątnych tego trójkąta jest równy
5:12.
Oblicz długość przeciwprostokątnej tego trójkąta.
Odpowiedź:
| c= | |
| Zadanie 13. 4 pkt ⋅ Numer: pp-31104 ⋅ Poprawnie: 17/189 [8%] | Rozwiąż |
Podpunkt 13.1 (2 pkt)
W trapezie prostokątnym ABCD dłuższa podstawa AB
ma długość 5. Krótsza przekątna AC ma długość
równą 4 i dzieli trapez na dwa trójkąty prostokątne (zobacz rysunek).
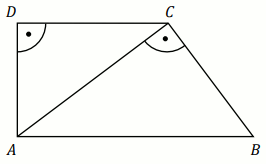

Oblicz |AD|.
Odpowiedź:
| |AD|= | |
Podpunkt 13.2 (2 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
| P_{ABCD}= | |