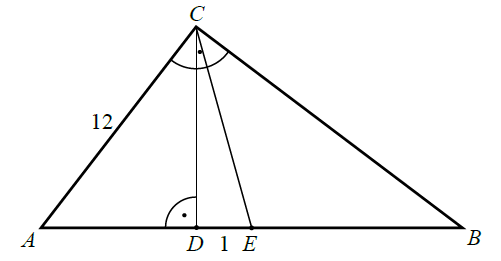Wysokości i środkowe w trójkącie
Zadania dla liceum ogólnokształcącego - poziom podstawowy
wysokości trójkąta
środkowe w trójkącie
ortocentrum
podział środkowych w stosunku 1:2
środek ciężkości trójkąta
Zadanie 1. 1 pkt ⋅ Numer: pp-10664 ⋅ Poprawnie: 97/158 [61%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
Kąt trójkąta prostokątnego ma miarę
59^{\circ} .
Z wierzchołka kąta prostego poprowadzono środkową i wysokość tego trójkąta.
Oblicz miarę stopniową kąta między nimi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 2. 1 pkt ⋅ Numer: pp-11695 ⋅ Poprawnie: 35/91 [38%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
Oblicz długość boku trójkąta równobocznego, którego wysokość ma długość
5\sqrt{10} .
Odpowiedź:
Zadanie 3. 1 pkt ⋅ Numer: pp-11696 ⋅ Poprawnie: 26/58 [44%]
Rozwiąż
Podpunkt 3.1 (1 pkt)
Oblicz długość boku trójkąta równobocznego więdząc, że jest on o
8
dłuższy od wysokości tego trójkąta.
Odpowiedź:
a=
+
\cdot
√
(wpisz trzy liczby całkowite)
Zadanie 4. 1 pkt ⋅ Numer: pp-11697 ⋅ Poprawnie: 12/30 [40%]
Rozwiąż
Podpunkt 4.1 (1 pkt)
«« Oblicz długość przyprostokątnej trójkąta prostokątnego równoramiennego więdząc, że jest ona o
20
dłuższa od najkrótszej wysokości tego trójkąta.
Odpowiedź:
a=
+
\cdot
√
(wpisz trzy liczby całkowite)
Zadanie 5. 1 pkt ⋅ Numer: pp-12098 ⋅ Poprawnie: 47/90 [52%]
Rozwiąż
Podpunkt 5.1 (1 pkt)
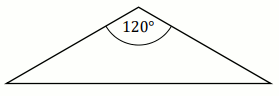
W pewnym trójkącie równoramiennym największy kąt ma miarę
120^{\circ} ,
a najdłuższy bok ma długość
38 (zobacz rysunek).
Najkrótsza wysokość tego trójkąta ma długość równą:
Odpowiedzi:
A. 19
B. \frac{19\sqrt{3}}{9}
C. \frac{19\sqrt{3}}{4}
D. \frac{19\sqrt{3}}{12}
E. \frac{19\sqrt{3}}{3}
F. \frac{19\sqrt{3}}{6}
Zadanie 6. 2 pkt ⋅ Numer: pp-20708 ⋅ Poprawnie: 100/201 [49%]
Rozwiąż
Podpunkt 6.1 (1 pkt)
» Wysokości trójkąta prostokątnego mają długości
\frac{48}{5} ,
16 i
12 . Wyznacz długości odcinków, na jakie wysokość
opuszczona na przeciwprostokątną podzieliła tę przeciwprostokątną.
Podaj długość krótszego z tych odcinków.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 6.2 (1 pkt)
Podaj długość dłuższego z tych odcinków.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 7. 2 pkt ⋅ Numer: pp-20709 ⋅ Poprawnie: 77/246 [31%]
Rozwiąż
Podpunkt 7.1 (1 pkt)
Dane są długości boków trójkąta
34 ,
50 i
56 . Zbadaj, czy
trójkąt ten jest prostokątny, ostrokątny czy rozwartokątny.
Jeśli trójkąt jest prostokątny wpisz 1 ,
jeśli ostrokątny wpisz 2 , jeśli rozwartokątny
wpisz 3 .
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Wyznacz długość wysokości opuszczonej na najdłuższy bok tego trójkąta.
Odpowiedź:
Zadanie 8. 2 pkt ⋅ Numer: pp-20710 ⋅ Poprawnie: 59/195 [30%]
Rozwiąż
Podpunkt 8.1 (2 pkt)
« W trójkącie
ABC kąt przy wierzchołku
A jest prosty oraz
|AB|=70 i
|AC|=24 . Odcinek
AE jest środkową tego trójkąta, zaś
odcinek
AF jego wysokością.
Oblicz |EF| .
Odpowiedź:
Zadanie 9. 2 pkt ⋅ Numer: pp-20711 ⋅ Poprawnie: 132/271 [48%]
Rozwiąż
Podpunkt 9.1 (2 pkt)
« W trójkącie
ABC kąt przy wierzchołku
A jest prosty oraz
|AB|=84 i
|AC|=13 .
Oblicz odległość środka ciężkości trójkąta ABC
od punktu A .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 10. 2 pkt ⋅ Numer: pp-20234 ⋅ Poprawnie: 51/183 [27%]
Rozwiąż
Podpunkt 10.1 (1 pkt)
« Z wierzchołków kątów ostrych trójkąta prostokątnego poprowadzono dwie
środkowe o długościach
5 i
6 .
Podaj długość krótszej z przyprostokątnych tego trójkąta.
Odpowiedź:
min=
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (1 pkt)
Podaj długość przeciwprostokątnej tego trójkąta.
Odpowiedź:
c=
(liczba zapisana dziesiętnie)
Zadanie 11. 2 pkt ⋅ Numer: pp-20236 ⋅ Poprawnie: 105/225 [46%]
Rozwiąż
Podpunkt 11.1 (2 pkt)
« Jedna z przyprostokątnych trójkąta prostokątnego ma długość
10 , a wysokość opuszczona na przeciwprostokątną
tego trójkata długość
5\sqrt{3} .
Oblicz długość drugiej przyprostokątnej tego trójkąta.
Odpowiedź:
b=
\cdot √
(wpisz dwie liczby całkowite)
Zadanie 12. 2 pkt ⋅ Numer: pp-20240 ⋅ Poprawnie: 73/182 [40%]
Rozwiąż
Podpunkt 12.1 (1 pkt)
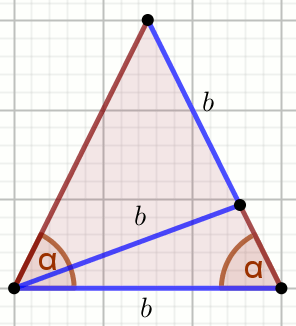
« Wyznacz miary kątów trójkąta pokazanego na rysunku:
Podaj miarę stopniową najmniejszego kąta tego trójkąta.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
Podaj miarę największego kąta tego trójkąta.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
Zadanie 13. 2 pkt ⋅ Numer: pp-20244 ⋅ Poprawnie: 59/154 [38%]
Rozwiąż
Podpunkt 13.1 (1 pkt)
W trójkącie prostokątnym najkrótszy bok ma długość
12 , a
najdłuższy bok jest dłuższy od dłuższej przyprostokątnej o
2 .
Oblicz długość dłuższej przyprostokątnej tego trójkąta.
Odpowiedź:
(wpisz dwie liczby całkowite)
Podpunkt 13.2 (1 pkt)
Oblicz odległość punktu przecięcia się środkowych tego trójkąta od
wierzchołka kąta prostego.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 14. 2 pkt ⋅ Numer: pp-20871 ⋅ Poprawnie: 29/41 [70%]
Rozwiąż
Podpunkt 14.1 (2 pkt)
Podstawa trójkąta równoramiennego ma długość
48 , a punkt
przecięcia się środkowych tego trójkąta znajduje się w odległości
\frac{70}{3} od tej podstawy.
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
Zadanie 15. 2 pkt ⋅ Numer: pp-21025 ⋅ Poprawnie: 29/87 [33%]
Rozwiąż
Podpunkt 15.1 (2 pkt)
W trójkącie równoramiennym o obwodzie
144 wysokość opuszczona na
podstawę ma długość
60 .
Oblicz długość ramienia tego trójkata.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
Zadanie 16. 4 pkt ⋅ Numer: pp-30022 ⋅ Poprawnie: 39/115 [33%]
Rozwiąż
Podpunkt 16.1 (4 pkt)
« W trójkącie dane są:
|AC|=30 oraz
|BC|=36 . Środkowe tego trójkata
AM i
BN
przecinają się pod kątem prostym.
Oblicz długość boku AB tego trójkąta.
Odpowiedź:
Zadanie 17. 4 pkt ⋅ Numer: pp-30299 ⋅ Poprawnie: 51/137 [37%]
Rozwiąż
Podpunkt 17.1 (2 pkt)
« W trójkącie
ABC dane są:
|AC|=74 ,
|BC|=74 i
|AB|=140 .
Wyznacz długości środkowych trójkąta
ABC .
Podaj długość najkrótszej z środkowych tego trójkąta.
Odpowiedź:
Podpunkt 17.2 (2 pkt)
Podaj długość najdłuższej z środkowych tego trójkąta.
Odpowiedź:
Zadanie 18. 4 pkt ⋅ Numer: pp-30135 ⋅ Poprawnie: 72/127 [56%]
Rozwiąż
Podpunkt 18.1 (4 pkt)
« Punkt
E jest środkiem przeciwprostokątnej
AB trójkąta
ABC .
Odcinek
DE ma długość 1, jak na rysunku.
Oblicz obwód trójkąta ABC .
Odpowiedź:
L_{\triangle ABC}=
+
\cdot
√
(wpisz trzy liczby całkowite)
☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat
Masz pytania? Napisz: k42195@poczta.fm