Symetria wykresu
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- symetria względem osi Ox
- symetria względem osi Oy
- symetria względem początku układu współrzędnych
- przekształcenia symetryczne wykresu funkcji
| Zadanie 1. 1 pkt ⋅ Numer: pp-11397 ⋅ Poprawnie: 295/523 [56%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=(7,+\infty) oraz
ZW_f=\langle -3,3). O funkcji
g wiadomo, że
g(x)=-f(x).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : D_g=(-7,+\infty) | T/N : D_g=(-\infty,-7,) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11398 ⋅ Poprawnie: 266/499 [53%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=\langle -6,-3\rangle oraz
ZW_f=\langle -7,+\infty). O funkcji
g wiadomo, że
g(x)=-f(x).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : D_g=\langle-6,-3\rangle | T/N : D_g=\langle3,6\rangle |
| T/N : ZW_g=(-\infty,-7) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10783 ⋅ Poprawnie: 409/519 [78%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku 1. jest przedstawiony wykres funkcji f,
a na rysunku 2. – wykres funkcji g.
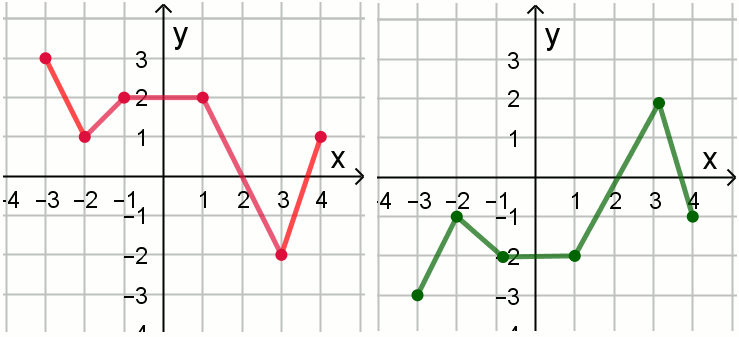

Funkcja g jest określona wzorem:
Odpowiedzi:
| A. g(x)=f(x)+4 | B. g(x)=f(x)-4 |
| C. g(x)=f(-x) | D. g(x)=-f(x) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10776 ⋅ Poprawnie: 205/612 [33%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku 1 jest przedstawiony wykres funkcji
y=f(x).
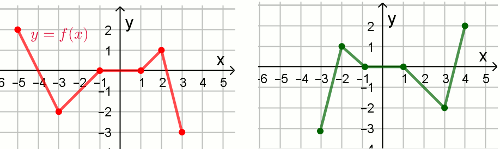

Funkcja przedstawiona na rysunku 2 jest określona wzorem:
Odpowiedzi:
| A. y=f(x-1) | B. żadnym z pozostałych wzorów |
| C. y=-f(x) | D. y=f(-x) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10785 ⋅ Poprawnie: 309/415 [74%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
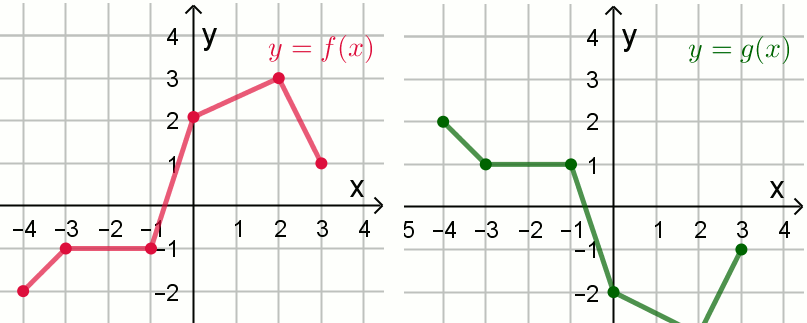
Funkcja g określona jest wzorem:
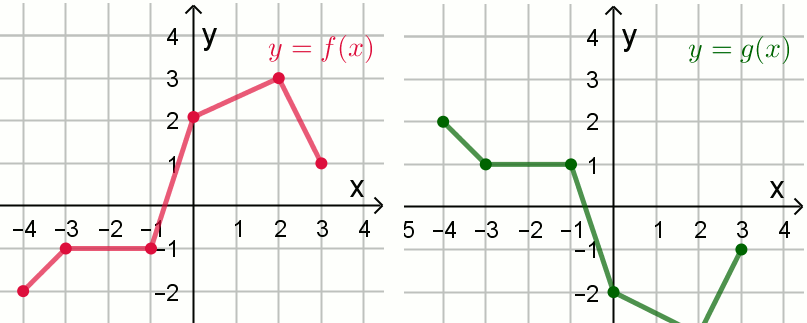
Odpowiedzi:
| A. g(x)=f(-x)-1 | B. g(x)=f(-x) |
| C. g(x)=-f(x) | D. g(x)=-f(-x) |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10786 ⋅ Poprawnie: 157/277 [56%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Na rysunku 1. przedstawiono wykres funkcji
y=f(x) (czerwony), a na rysunku 2.
wykres funkcji y=g(x) (zielony):
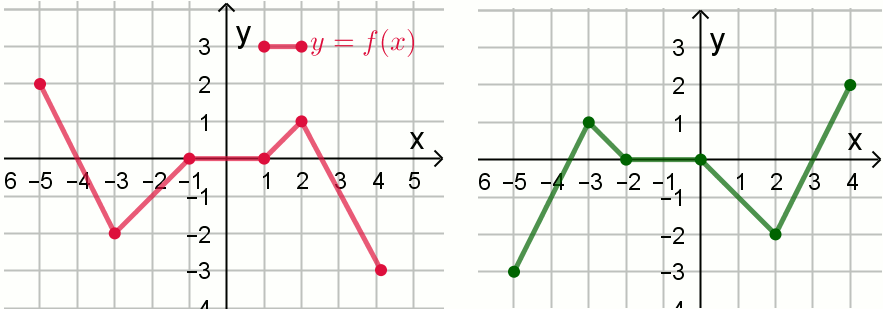
Funkcja g określona jest wzorem:
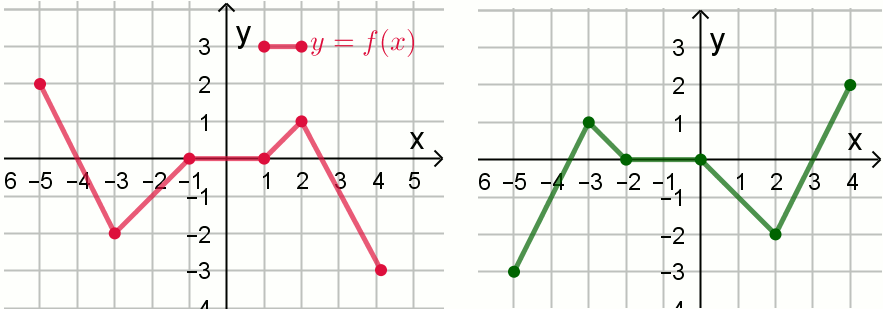
Odpowiedzi:
| A. g(x)=f(1-x) | B. g(x)=f(-1-x) |
| C. g(x)=f(-x) | D. g(x)=-f(-x) |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10768 ⋅ Poprawnie: 204/319 [63%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
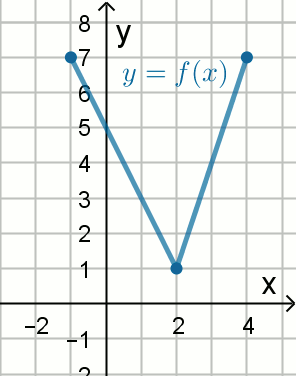
Funkcja, której wykres jest symetryczny do tego wykresu względem osi Ox określona jest wzorem:

Odpowiedzi:
| A. y=f(-x)-1 | B. y=f(-x)+1 |
| C. y=f(-x) | D. g(x)=-f(x) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10767 ⋅ Poprawnie: 206/284 [72%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
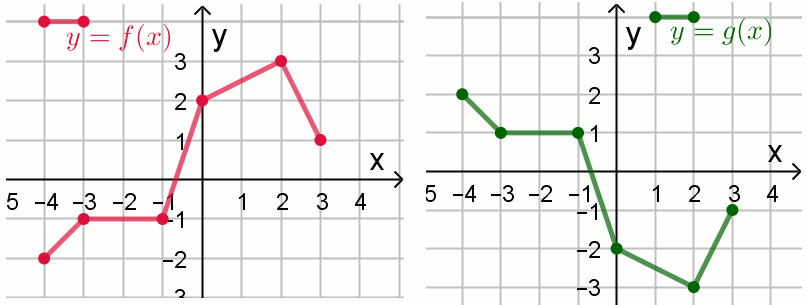
Funkcja g określona jest wzorem:
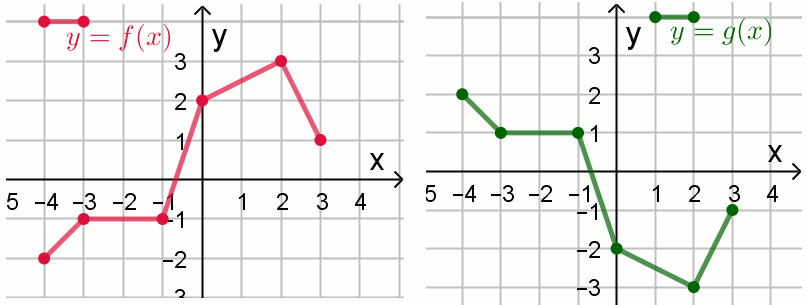
Odpowiedzi:
| A. g(x)=-f(x) | B. g(x)=-f(-x) |
| C. g(x)=f(x-1) | D. g(x)=f(-x) |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10779 ⋅ Poprawnie: 510/662 [77%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
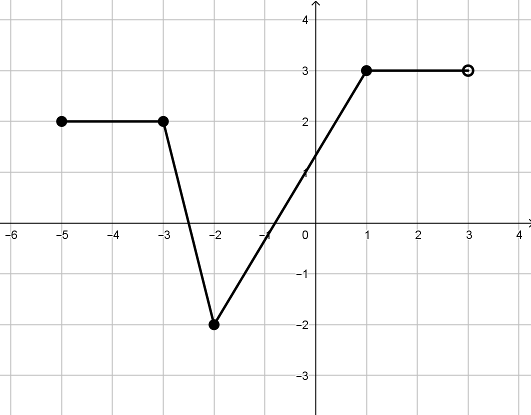
Dziedziną funkcji y=-f(x) jest zbiór:

Odpowiedzi:
| A. (-3,5\rangle | B. \langle -5,3\rangle |
| C. \langle -5,3) | D. \langle -3,5\rangle |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10781 ⋅ Poprawnie: 193/257 [75%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« Funkcja f ma n=3 miejsc zerowych.
Ile miejsc zerowych ma funkcja określona wzorem g(x)=-f(x+8)?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 1 pkt ⋅ Numer: pp-10782 ⋅ Poprawnie: 175/318 [55%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x), której miejscem zerowym jest liczba
1 oraz f(0)=-2:
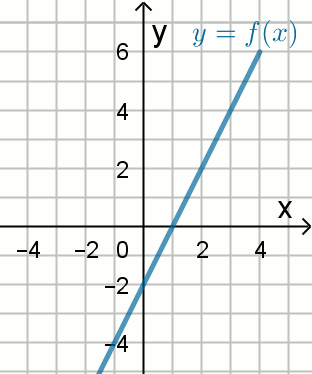
Wskaż funkcję, której wykres jest symetryczny do tego wykresu względem osi Ox:

Odpowiedzi:
| A. y=-2x+2 | B. y=2x+2 |
| C. y=-2x-2 | D. y=2x-2 |
| Zadanie 12. 1 pkt ⋅ Numer: pp-11395 ⋅ Poprawnie: 302/494 [61%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=7x^2-3x przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=ax^2+bx.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 13. 1 pkt ⋅ Numer: pp-11747 ⋅ Poprawnie: 35/41 [85%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=8x+5 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=ax+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11748 ⋅ Poprawnie: 40/47 [85%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=3\sqrt{x}+8 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=a\sqrt{x}+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 15. 1 pkt ⋅ Numer: pp-11749 ⋅ Poprawnie: 39/44 [88%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=8|x|+5 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=a|x|+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 16. 1 pkt ⋅ Numer: pp-11396 ⋅ Poprawnie: 167/457 [36%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=8x^2+5x przez symetrię względem osi
Oy otrzymamo wykres funkcji określonej
wzorem y=ax^2+bx.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 17. 1 pkt ⋅ Numer: pp-11745 ⋅ Poprawnie: 21/27 [77%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=8x+5 przez symetrię względem osi
Oy otrzymamo wykres funkcji określonej
wzorem y=ax+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 18. 1 pkt ⋅ Numer: pp-10784 ⋅ Poprawnie: 389/678 [57%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
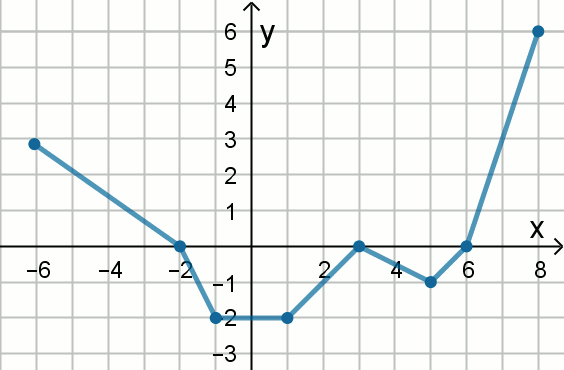

Zbiorem wartości funkcji y=-f(-x) jest przedział liczbowy \langle p, q\rangle.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 19. 1 pkt ⋅ Numer: pp-10766 ⋅ Poprawnie: 410/588 [69%] | Rozwiąż |
Podpunkt 19.1 (1 pkt)
Na rysunku 1 jest przedstawiony wykres funkcji
y=f(x).
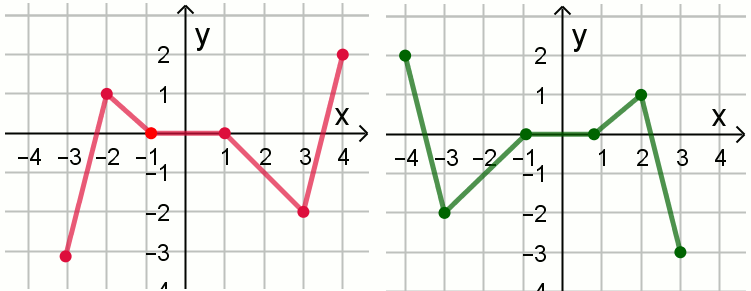
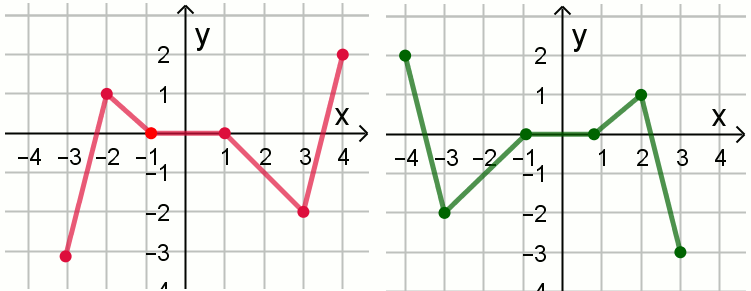
Funkcja przedstawiona na rysunku 2 jest określona wzorem:
Odpowiedzi:
| A. y=f(x-1) | B. y=f(-x) |
| C. y=-f(x) | D. y=-1+f(x) |
| Zadanie 20. 1 pkt ⋅ Numer: pp-11611 ⋅ Poprawnie: 1/31 [3%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
««Liczby -3 i 7 są miejscami zerowymi funkcji
f. Liczby x_1 i x_2
są miejscami zerowymi funkcji określonej wzorem g(x)=f(-x+3), przy czym
x_1\lessdot x_2.
Podaj liczby x_1 i x_2.
Odpowiedzi:
| x_1 | = |
(wpisz liczbę zapisaną dziesiętnie) |
| x_2 | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 21. 1 pkt ⋅ Numer: pp-11744 ⋅ Poprawnie: 1/6 [16%] | Rozwiąż |
Podpunkt 21.1 (1 pkt)
Liczby 3 i 5 są miejscami zerowymi funkcji
f. Liczby x_1 i x_2
są miejscami zerowymi funkcji określonej wzorem g(x)=-f(x-4), przy czym
x_1\lessdot x_2.
Podaj liczby x_1 i x_2.
Odpowiedzi:
| x_1 | = |
(wpisz liczbę zapisaną dziesiętnie) |
| x_2 | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 22. 1 pkt ⋅ Numer: pp-11929 ⋅ Poprawnie: 112/189 [59%] | Rozwiąż |
Podpunkt 22.1 (1 pkt)
Obrazem prostej o równaniu y=5x-2 w symetrii osiowej
względem osi Ox jest prosta o równaniu:
Odpowiedzi:
| A. y=-\frac{1}{5}x-2 | B. y=-5x-2 |
| C. y=\frac{1}{5}x-2 | D. y=-\frac{1}{5}x+2 |
| E. y=5x+2 | F. y=-5x+2 |