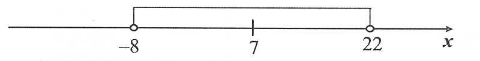Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Proste nierówności liniowe z wartością bezwzględną

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-10189 ⋅ Poprawnie: 395/726 [54%] Rozwiąż 
Podpunkt 1.1 (0.2 pkt)
 Rozwiązaniem nierówności
|x-6| \geqslant 6
jest zbiór liczbowy postaci:
Odpowiedzi:
A. \langle p,q\rangle B. (p,q\rangle
C. \langle p,+\infty) D. (-\infty,p)\cup(q,+\infty)
E. (p,q) F. (-\infty,p\rangle \cup \langle q,+\infty)
Podpunkt 1.2 (0.8 pkt)
 Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min= (wpisz liczbę całkowitą)
Zadanie 2.  1 pkt ⋅ Numer: pp-10186 ⋅ Poprawnie: 286/593 [48%] Rozwiąż 
Podpunkt 2.1 (0.2 pkt)
 » Rozwiązaniem nierówności |x+6| \lessdot 6 jest zbiór liczb postaci:
Odpowiedzi:
A. (-\infty,p)\cup(q,+\infty) B. (-\infty,p\rangle \cup \langle q,+\infty)
C. \langle p,q\rangle D. \langle p,q)
E. (p,q) F. (p,q\rangle
Podpunkt 2.2 (0.8 pkt)
 Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min= (wpisz liczbę całkowitą)
Zadanie 3.  1 pkt ⋅ Numer: pp-10188 ⋅ Poprawnie: 287/491 [58%] Rozwiąż 
Podpunkt 3.1 (0.2 pkt)
 Rozwiązaniem nierówności |x-2| \leqslant 3 jest zbiór liczb postaci:
Odpowiedzi:
A. \langle p,q\rangle B. (-\infty,p)\cup(q,+\infty)
C. \langle p,+\infty) D. (p,q)
E. (-\infty,q\rangle F. (-\infty,p\rangle \cup \langle q,+\infty)
Podpunkt 3.2 (0.8 pkt)
 Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min= (wpisz liczbę całkowitą)
Zadanie 4.  1 pkt ⋅ Numer: pr-10049 ⋅ Poprawnie: 61/108 [56%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 « Ile liczb całkowitych należy do dziedziny równania \frac{x^2-6}{\sqrt{6-x}}+\sqrt{8-|x|}=0?
Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 5.  1 pkt ⋅ Numer: pp-10191 ⋅ Poprawnie: 384/597 [64%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 « Wskaż nierówność, której rozwiązaniem jest zbiór \left(-\infty,-\frac{1}{2}\right)\cup\left(\frac{7}{2},+\infty\right) :
Odpowiedzi:
A. \left|x-\frac{3}{2}\right| > 2 B. \left|x+\frac{3}{2}\right| \leqslant 2
C. \left|x+\frac{3}{2}\right| > 2 D. \left|x-\frac{3}{2}\right| \lessdot 2
Zadanie 6.  1 pkt ⋅ Numer: pp-10194 ⋅ Poprawnie: 277/401 [69%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 Suma przedziałów (-\infty, 3\rangle\cup \langle 13,+\infty)

jest zbiorem rozwiązań nierówności:

Odpowiedzi:
A. \left|x-8\right| \leqslant 5 B. \left|x-8\right| \geqslant 5
C. \left|x-8\right| \lessdot 5 D. \left|x-8\right| > 5
Zadanie 7.  1 pkt ⋅ Numer: pp-10187 ⋅ Poprawnie: 560/894 [62%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
Odpowiedzi:
A. |x-7| \lessdot 15 B. |x-15| \lessdot 7
C. |x-15| > 7 D. |x-7| > 15
Zadanie 8.  1 pkt ⋅ Numer: pr-11592 ⋅ Poprawnie: 57/139 [41%] Rozwiąż 
Podpunkt 8.1 (0.2 pkt)
 Rozwiązaniem nierówności \left|x-\frac{13}{5}\right|-8,4\leqslant 0 jest zbiór postaci:
Odpowiedzi:
A. (-\infty, p)\cup (q,+\infty) B. (-\infty, q\rangle
C. \langle p,q\rangle D. \langle p,+\infty)
E. (p,q) F. (-\infty, p\rangle\cup \langle q,+\infty)
Podpunkt 8.2 (0.8 pkt)
 Zapisz rozwiązanie tej nierówności w postaci sumy przedziałów.

Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (wpisz liczbę zapisaną dziesiętnie)
max= (wpisz liczbę zapisaną dziesiętnie)
Zadanie 9.  1 pkt ⋅ Numer: pr-11593 ⋅ Poprawnie: 63/83 [75%] Rozwiąż 
Podpunkt 9.1 (0.2 pkt)
 Rozwiązaniem nierówności \left|-\frac{7}{4}+x\right|\geqslant 1,25 jest zbiór postaci:
Odpowiedzi:
A. (-\infty, p)\cup (q,+\infty) B. \langle p,q\rangle
C. (-\infty, p\rangle\cup \langle q,+\infty) D. \langle p,+\infty)
E. (-\infty, q\rangle F. (p,q)
Podpunkt 9.2 (0.8 pkt)
 Zapisz rozwiązanie tej nierówności w postaci sumy przedziałów.

Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (wpisz liczbę zapisaną dziesiętnie)
max= (wpisz liczbę zapisaną dziesiętnie)
Zadanie 10.  1 pkt ⋅ Numer: pr-11594 ⋅ Poprawnie: 12/20 [60%] Rozwiąż 
Podpunkt 10.1 (0.2 pkt)
 Rozwiązaniem nierówności \left|x-\sqrt{2}-1\right| > 1 jest zbiór postaci:
Odpowiedzi:
A. \langle p,q\rangle B. (-\infty, q\rangle
C. \langle p,+\infty) D. (p,q)
E. (-\infty, p\rangle\cup \langle q,+\infty) F. (-\infty, p)\cup (q,+\infty)
Podpunkt 10.2 (0.8 pkt)
 Zapisz rozwiązanie tej nierówności w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:  + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 11.  1 pkt ⋅ Numer: pr-11716 ⋅ Poprawnie: 10/19 [52%] Rozwiąż 
Podpunkt 11.1 (0.2 pkt)
 « Rozwiązaniem nierówności \left|x+\sqrt{3}-1\right| \lessdot 4 jest zbiór postaci:
Odpowiedzi:
A. (-\infty, q\rangle B. (-\infty, p)\cup (q,+\infty)
C. \langle p,+\infty) D. \langle p,q\rangle
E. (-\infty, p\rangle\cup \langle q,+\infty) F. (p,q)
Podpunkt 11.2 (0.8 pkt)
 Zapisz rozwiązanie tej nierówności w postaci sumy przedziałów. Podaj najmniejszym z końców liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:  + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 12.  1 pkt ⋅ Numer: pr-11595 ⋅ Poprawnie: 10/21 [47%] Rozwiąż 
Podpunkt 12.1 (0.2 pkt)
 Rozwiązaniem nierówności \left|x+\sqrt{3}-1\right| \leqslant 4 jest zbiór postaci:
Odpowiedzi:
A. (-\infty, p\rangle\cup \langle q,+\infty) B. (p,q)
C. (-\infty, p)\cup (q,+\infty) D. \langle p,q\rangle
E. (-\infty, q\rangle F. \langle p,+\infty)
Podpunkt 12.2 (0.8 pkt)
 Zapisz rozwiązanie tej nierówności w postaci sumy przedziałów. Podaj najmniejszym z końców liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:  + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 13.  1 pkt ⋅ Numer: pp-10190 ⋅ Poprawnie: 282/480 [58%] Rozwiąż 
Podpunkt 13.1 (0.2 pkt)
 « Rozwiązaniem nierówności
|x+6| > 6
jest zbiór liczbowy postaci:
Odpowiedzi:
A. (-\infty,p\rangle \cup \langle q,+\infty) B. \langle p,q\rangle
C. (p,+\infty) D. \langle p,q)
E. (p,q) F. (-\infty,p)\cup(q,+\infty)
Podpunkt 13.2 (0.8 pkt)
 Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min= (wpisz liczbę całkowitą)
Zadanie 14.  1 pkt ⋅ Numer: pp-10192 ⋅ Poprawnie: 136/323 [42%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
 « Wyznacz największą liczbę całkowitą dodatnią spełniającą nierówność |x+6| \lessdot 19.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 15.  1 pkt ⋅ Numer: pp-11722 ⋅ Poprawnie: 10/10 [100%] Rozwiąż 
Podpunkt 15.1 (0.5 pkt)
 Rozwiąż nierówność |12x-26|\lessdot 50.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.

Odpowiedź:
x_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 15.2 (0.5 pkt)
 Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{max}=
(wpisz dwie liczby całkowite)
Zadanie 16.  1 pkt ⋅ Numer: pp-11717 ⋅ Poprawnie: 24/58 [41%] Rozwiąż 
Podpunkt 16.1 (0.5 pkt)
 Rozwiąż nierówność |65-6x|\geqslant 5.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.

Odpowiedź:
x_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 16.2 (0.5 pkt)
 Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{max}=
(wpisz dwie liczby całkowite)
Zadanie 17.  1 pkt ⋅ Numer: pp-11718 ⋅ Poprawnie: 19/24 [79%] Rozwiąż 
Podpunkt 17.1 (0.5 pkt)
 Rozwiąż nierówność 1-|2x-9|\leqslant 0.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.

Odpowiedź:
x_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 17.2 (0.5 pkt)
 Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{max}=
(wpisz dwie liczby całkowite)
Zadanie 18.  1 pkt ⋅ Numer: pp-11719 ⋅ Poprawnie: 23/26 [88%] Rozwiąż 
Podpunkt 18.1 (0.5 pkt)
 Rozwiąż nierówność 3-|-13-5x| > 0.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.

Odpowiedź:
x_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 18.2 (0.5 pkt)
 Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{max}=
(wpisz dwie liczby całkowite)
Zadanie 19.  1 pkt ⋅ Numer: pp-10685 ⋅ Poprawnie: 107/145 [73%] Rozwiąż 
Podpunkt 19.1 (1 pkt)
 Wyznacz dziedzinę funkcji g(x)=\sqrt{|x+5|-3}. Rozwiązanie zapisz w postaci sumy przedziałów. Liczby m i M są odpowiednio najmniejszym i największym z końców liczbowych tych przedziałów.

Podaj liczby m i M.

Odpowiedzi:
m= (wpisz liczbę całkowitą)
M= (wpisz liczbę całkowitą)
Zadanie 20.  1 pkt ⋅ Numer: pp-11757 ⋅ Poprawnie: 639/838 [76%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
 Zbiór A=(-\infty, -1\rangle\cup\langle 4,+\infty) jest rozwiązaniem nierówności:
Odpowiedzi:
A. \left|x-\frac{3}{2}\right|\geqslant \frac{5}{2} B. \left|x-\frac{3}{2}\right|\leqslant \frac{5}{2}
C. \left|x+\frac{3}{2}\right|\leqslant \frac{5}{2} D. \left|x-\frac{3}{2}\right|\geqslant \frac{7}{2}
E. \left|x+\frac{3}{2}\right|\geqslant \frac{5}{2} F. \left|x-\frac{3}{2}\right|\leqslant \frac{7}{2}
Zadanie 21.  1 pkt ⋅ Numer: pp-11778 ⋅ Poprawnie: 489/900 [54%] Rozwiąż 
Podpunkt 21.1 (1 pkt)
 Wszystkich liczb całkowitych dodatnich spełniających nierówność |x+6|\lessdot 11 jest:
Odpowiedzi:
A. 17 B. 5
C. 18 D. 4
Zadanie 22.  1 pkt ⋅ Numer: pp-11804 ⋅ Poprawnie: 555/716 [77%] Rozwiąż 
Podpunkt 22.1 (1 pkt)
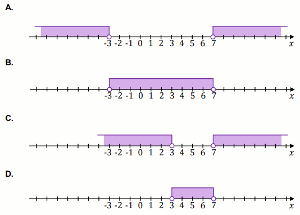
 Dana jest nierówność |x-5| > 2 oraz zbiory zaznaczone na osi liczbowej:

Rozwiązanie tej nierówności pokazano na rysunku:

Odpowiedzi:
A. C B. D
C. B D. A
Zadanie 23.  1 pkt ⋅ Numer: pp-11832 ⋅ Poprawnie: 449/665 [67%] Rozwiąż 
Podpunkt 23.1 (1 pkt)
 Przedział liczbowy (-4, 2) jest rozwiązaniem nierówności:
Odpowiedzi:
A. |x-3|\lessdot 1 B. |x|>3
C. |x+3|\lessdot 1 D. |x-1|\lessdot 3
E. |x+1|>3 F. |x+1|\lessdot 3
Zadanie 24.  1 pkt ⋅ Numer: pp-11980 ⋅ Poprawnie: 373/587 [63%] Rozwiąż 
Podpunkt 24.1 (1 pkt)
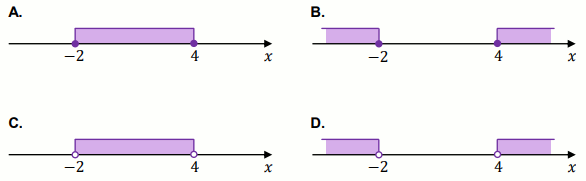
 Dana jest nierówność |x-1|\leqslant 3.

Na którym rysunku poprawnie zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających powyższą nierówność?

Odpowiedzi:
A. C B. A
C. D D. B
Zadanie 25.  1 pkt ⋅ Numer: pp-12135 ⋅ Poprawnie: 105/125 [84%] Rozwiąż 
Podpunkt 25.1 (1 pkt)
 Liczba wszystkich całkowitych rozwiązań nierówności |x-4| < 4 jest równa:
Odpowiedzi:
A. 11 B. 12
C. 8 D. 7
E. 5 F. 3
Zadanie 26.  2 pkt ⋅ Numer: pp-20920 ⋅ Poprawnie: 27/70 [38%] Rozwiąż 
Podpunkt 26.1 (2 pkt)
 Rozwiąż nierówność podwójną |x+5|\leqslant 3\leqslant|x+6|+1.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (wpisz liczbę zapisaną dziesiętnie)
max= (wpisz liczbę zapisaną dziesiętnie)
Zadanie 27.  2 pkt ⋅ Numer: pp-21034 ⋅ Poprawnie: 14/16 [87%] Rozwiąż 
Podpunkt 27.1 (2 pkt)
 Rozwiąż nierówność podwójną 2-|2x-7|\leqslant 2|-7+2x|\leqslant 4.

Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy i największy z końców liczbowych tych przedziałów.

Odpowiedzi:
min= (wpisz liczbę zapisaną dziesiętnie)
max= (wpisz liczbę zapisaną dziesiętnie)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm