⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Funkcja kwadratowa - postać kanoniczna
Zadania dla klasy drugiej liceum ogólnokształcącego - poziom podstawowy
- funkcja kwadratowa
- postać kanoniczna funkcji kwadratowej
- wektor przesunięcia
- funkcja postaci y=f(x-p)+q
| Zadanie 1. 1 pkt ⋅ Numer: pp-11031 ⋅ Poprawnie: 419/591 [70%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Wierzchołkiem paraboli, która jest wykresem funkcji f
jest punkt W=(-3,4).
Wówczas:
Odpowiedzi:
| T/N : f(-6)=f(0) | T/N : f(-9)=f(3) |
| T/N : f(-7)=f(2) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10989 ⋅ Poprawnie: 706/1015 [69%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Największą wartością funkcji kwadratowej
f(x)=-4(x-2)^2-3 jest ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10990 ⋅ Poprawnie: 263/409 [64%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Funkcja f(x)=x^2-12x+36
dla argumentu \sqrt{6} przyjmuje wartość
\left(......\cdot\sqrt{6}-6\right)^2.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10993 ⋅ Poprawnie: 572/825 [69%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Funkcja kwadratowa określona jest wzorem
f(x)=x^2-8x+c.
Jeżeli f(2)=-16, to f(1)=..........
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-11059 ⋅ Poprawnie: 251/430 [58%] | Rozwiąż |
Podpunkt 5.1 (0.5 pkt)
Parabola y=(4+3x)^2-3
ma wierzchołek w punkcie o współrzędnych \left(x_w,y_w\right).
Wyznacz współrzędną x_w.
Odpowiedź:
| x_w= | |
Podpunkt 5.2 (0.5 pkt)
Wyznacz współrzędną y_w.
Odpowiedź:
| y_w= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11072 ⋅ Poprawnie: 341/556 [61%] | Rozwiąż |
Podpunkt 6.1 (0.5 pkt)
« O funkcji kwadratowej opisanej wzorem f(x)=a(x-p)^2+q wiadomo, że ma dwa
miejsca zerowe 3 i 7 oraz
że najmniejszą jej wartością jest liczba -2.
Wyznacz wartość parametru a.
Odpowiedź:
| a= | |
Podpunkt 6.2 (0.5 pkt)
Wyznacz wartość parametru p.
Odpowiedź:
| p= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11002 ⋅ Poprawnie: 730/998 [73%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Funkcja kwadratowa
f(x)=x^2+bx+c jest malejąca dla
x\in(-\infty,-2\rangle, a zbiorem jej wartości
jest przedział \langle 3,+\infty).
Postać kanoniczna tej funkcji opisana jest wzorem y=(x-p)^2+q.
Podaj wartości parametrów p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11012 ⋅ Poprawnie: 642/967 [66%] | Rozwiąż |
Podpunkt 8.1 (0.5 pkt)
Postać kanoniczna trójmianu kwadratowego
y=3x^2-24x+\frac{145}{3}
opisana jest wzorem y=a(x-p)^2+q.
Podaj wartość parametru p.
Odpowiedź:
p=
(wpisz liczbę całkowitą)
Podpunkt 8.2 (0.5 pkt)
Podaj wartość parametru q.
Odpowiedź:
| q= | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11430 ⋅ Poprawnie: 986/1244 [79%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Wykresem funkcji kwadratowej f(x)=x^2-2x+2
jest parabola, której wierzchołkiem jest punkt o współrzędnych
\left(x_w, y_w\right).
Podaj współrzędne wierzchołka paraboli x_w i y_w.
Odpowiedzi:
| x_w | = |
(wpisz liczbę całkowitą) |
| y_w | = |
(wpisz liczbę całkowitą) |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10979 ⋅ Poprawnie: 178/326 [54%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Dana jest funkcja f określona wzorem f(x)=-8(x-1)^2+1.
Wyznacz największą wartość funkcji określonej wzorem h(x)=f(x+3)+5.
Odpowiedź:
h_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 11. 1 pkt ⋅ Numer: pp-10983 ⋅ Poprawnie: 303/536 [56%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Wierzchołek paraboli y=x^2-4x leży na prostej
o równaniu:
Odpowiedzi:
| A. y=-4x | B. y=-1x |
| C. y=4x | D. y=1x |
| E. y=-2x | F. y=2x |
| Zadanie 12. 1 pkt ⋅ Numer: pp-10991 ⋅ Poprawnie: 198/343 [57%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Zbiorem wartości funkcji kwadratowej
f(x)=-x^2+ax-\frac{a^2}{4}-a jest przedział
(-\infty,5\rangle.
Wyznacz wartość parametru a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 13. 1 pkt ⋅ Numer: pp-11003 ⋅ Poprawnie: 549/915 [60%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
» Wskaż funkcję kwadratową rosnąca w przedziale
(-\infty,-2\rangle:
Odpowiedzi:
| A. y=(x+2)^2+3 | B. y=-(x+3)^2+2 |
| C. y=-(x+2)^2+3 | D. y=-(x-3)^2-\frac{3}{2} |
| E. y=(x-2)^2+3 | F. y=-(x+3)^2-2 |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11052 ⋅ Poprawnie: 817/1146 [71%] | Rozwiąż |
Podpunkt 14.1 (0.8 pkt)
Zbiorem wartości funkcji kwadratowej
y=-x^2-4 x-1 jest pewien przedział liczbowy.
Podaj ten koniec tego przedziału, który jest liczbą całkowitą.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 14.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. \frac{3}{4} | B. -\infty |
| C. \frac{1}{2} | D. -\frac{3}{4} |
| E. +\infty | F. -\frac{1}{2} |
| Zadanie 15. 1 pkt ⋅ Numer: pp-11005 ⋅ Poprawnie: 359/563 [63%] | Rozwiąż |
Podpunkt 15.1 (0.2 pkt)
« Funkcja y=-(x+2)^2+3 jest rosnąca w pewnym
przedziale liczbowym.
Przedział ten ma postać:
Odpowiedzi:
| A. (p,q) | B. \langle p,+\infty) |
| C. (-\infty,p\rangle | D. (-\infty,p) |
| E. \langle p,q\rangle | F. (p,+\infty) |
Podpunkt 15.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 16. 1 pkt ⋅ Numer: pp-11006 ⋅ Poprawnie: 350/652 [53%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
« Wskaż funkcję, która w przedziale
(-\infty,-2) jest malejąca:
Odpowiedzi:
| A. y=-(x+2)^2-3 | B. y=(x-2)^2+3 |
| C. y=-(x-2)^2-2 | D. y=(x-3)^2-2 |
| E. y=(x+3)^2-2 | F. y=(x+2)^2+3 |
| Zadanie 17. 1 pkt ⋅ Numer: pp-11009 ⋅ Poprawnie: 212/393 [53%] | Rozwiąż |
Podpunkt 17.1 (0.2 pkt)
« Maksymalny zbiór, w którym funkcja kwadratowa
f(x)=-3(x+2)^2+3 jest rosnąca jest pewnym przedziałem liczbowym.
Przedział ten ma postać:
Odpowiedzi:
| A. (p,+\infty) | B. (p,q) |
| C. \langle p,q\rangle | D. \langle p,+\infty) |
| E. (-\infty,p\rangle | F. (-\infty,p) |
Podpunkt 17.2 (0.8 pkt)
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 18. 1 pkt ⋅ Numer: pp-11030 ⋅ Poprawnie: 900/1174 [76%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział
\langle 2,+\infty):
Odpowiedzi:
| A. y=(x+1)^2-2 | B. y=-(x-5)^2+2 |
| C. y=-(x+2)^2+2 | D. y=-2(x+6)^2-2 |
| E. y=(x-1)^2-2 | F. y=(x+3)^2+2 |
| Zadanie 19. 1 pkt ⋅ Numer: pp-11028 ⋅ Poprawnie: 610/795 [76%] | Rozwiąż |
Podpunkt 19.1 (1 pkt)
Osią symetrii paraboli o równaniu
y=-8x^2-248x-264 jest prosta określona:
równaniem x=..........
Podaj brakującą liczbę.
Odpowiedź:
| x= | |
| Zadanie 20. 1 pkt ⋅ Numer: pp-11029 ⋅ Poprawnie: 234/355 [65%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
» Prosta o równaniu 4x+3=0 jest osią symetrii
paraboli:
Odpowiedzi:
| A. y=-2x^2-1x-4 | B. y=-4x^2+\frac{9}{2}x-4 |
| C. y=-2x^2+1x-4 | D. y=-2x^2-3x-4 |
| E. y=-2x^2-\frac{3}{2}x-4 | F. y=-4x^2-\frac{9}{2}x-4 |
| Zadanie 21. 1 pkt ⋅ Numer: pp-11008 ⋅ Poprawnie: 400/563 [71%] | Rozwiąż |
Podpunkt 21.1 (0.8 pkt)
« Zbiorem wartości funkcji kwadratowej
f(x)=-x^2-\sqrt{2} jest pewnien przedział liczbowy.
Podaj ten koniec tego przedziału, który jest liczbą niewymierną.
Odpowiedź:
m\sqrt{n}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 21.2 (0.2 pkt)
Przedział ten ma postać:
Odpowiedzi:
| A. \left\langle p, q \right\rangle | B. \left(p, q\right) |
| C. \left\langle p,+\infty\right) | D. \left(-\infty,p\right\rangle |
| Zadanie 22. 1 pkt ⋅ Numer: pp-11032 ⋅ Poprawnie: 205/354 [57%] | Rozwiąż |
Podpunkt 22.1 (1 pkt)
Funkcja kwadratowa g spełnia warunek
g(-3)=g(4). Osią symetrii wykresu tej funkcji
jest prosta określona równaniem x+m=0.
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 23. 1 pkt ⋅ Numer: pp-11037 ⋅ Poprawnie: 210/336 [62%] | Rozwiąż |
Podpunkt 23.1 (1 pkt)
« Gdy przesuniemy wykres funkcji f(x)=x^2+\frac{1}{2} o
p=4 jednostek w lewo i q=10 jednostek w dół,
to otrzymamy wykres funkcji:
Odpowiedzi:
| A. y=(x-4)^2-\frac{19}{2} | B. y=(x-4)^2+\frac{21}{2} |
| C. y=(x+10)^2+\frac{9}{2} | D. y=(x+4)^2-\frac{19}{2} |
| Zadanie 24. 1 pkt ⋅ Numer: pp-11038 ⋅ Poprawnie: 136/229 [59%] | Rozwiąż |
Podpunkt 24.1 (1 pkt)
Gdy przesuniemy wykres funkcji f(x)=-2(x-4)^2-\frac{5}{2} o
p=6 jednostek w lewo i q=12 jednostek w górę,
to otrzymamy wykres funkcji:
Odpowiedzi:
| A. y=-2(x+2)^2-\frac{29}{2} | B. y=-2(x+2)^2+\frac{19}{2} |
| C. y=-2(x-10)^2+\frac{19}{2} | D. y=-2(x+8)^2+\frac{7}{2} |
| Zadanie 25. 1 pkt ⋅ Numer: pp-11039 ⋅ Poprawnie: 241/289 [83%] | Rozwiąż |
Podpunkt 25.1 (1 pkt)
Punkt (-3,4) jest wierzchołkiem paraboli.
Punkt o współrzędnych P=(0,-3) należy do tej
paraboli.
Zatem zbiorem wartości funkcji, której wykresem jest ta parabola jest:
Odpowiedzi:
| A. (-\infty,4\rangle | B. \langle 3,+\infty) |
| C. (-\infty,3\rangle | D. \langle -3,+\infty) |
| Zadanie 26. 1 pkt ⋅ Numer: pp-11040 ⋅ Poprawnie: 241/405 [59%] | Rozwiąż |
Podpunkt 26.1 (1 pkt)
Punkt P=(-3,4) należy do wykresu funkcji
g(x)=x^2-mx+1.
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 27. 1 pkt ⋅ Numer: pp-11044 ⋅ Poprawnie: 142/223 [63%] | Rozwiąż |
Podpunkt 27.1 (1 pkt)
Wykres funkcji kwadratowej g przecina oś
Ox w dwóch punktach.
Funkcja g opisana jest wzorem:
Odpowiedzi:
| A. g(x)=7(x+8)^2+7 | B. g(x)=9(x+4)^2+9 |
| C. g(x)=-11(x+11)^2-4 | D. g(x)=-3(x+4)^2+\sqrt{6} |
| Zadanie 28. 1 pkt ⋅ Numer: pp-11056 ⋅ Poprawnie: 610/801 [76%] | Rozwiąż |
Podpunkt 28.1 (1 pkt)
Parabola o wierzchołku P=(-3,4) i ramionach
skierowanych w dół może być wykresem funkcji określonej wzorem:
Odpowiedzi:
| A. y=(x+3)^2-4 | B. y=-2(x+3)^2+4 |
| C. y=3(x-4)^2+4 | D. y=-2(x-3)^2+4 |
| Zadanie 29. 1 pkt ⋅ Numer: pp-11063 ⋅ Poprawnie: 179/291 [61%] | Rozwiąż |
Podpunkt 29.1 (1 pkt)
« Funkcja f(x)=2x^2-8x+18 nie przyjmuje wartości:
Odpowiedzi:
| A. \frac{10\cdot\pi}{3} | B. \frac{20+\sqrt{2}}{2} |
| C. 5\sqrt{7} | D. \frac{\sqrt{2}}{5} |
| Zadanie 30. 1 pkt ⋅ Numer: pp-11060 ⋅ Poprawnie: 140/194 [72%] | Rozwiąż |
Podpunkt 30.1 (1 pkt)
Wierzchołek paraboli o równaniu y=(x+1)^2+2m+8
należy do prostej o równaniu y=1.
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 31. 1 pkt ⋅ Numer: pp-11061 ⋅ Poprawnie: 99/146 [67%] | Rozwiąż |
Podpunkt 31.1 (1 pkt)
» Oblicz odległość wierzchołka paraboli o równaniu
y=x^2+x+\frac{9}{4} od osi
Ox.
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 32. 1 pkt ⋅ Numer: pp-11071 ⋅ Poprawnie: 119/136 [87%] | Rozwiąż |
Podpunkt 32.1 (1 pkt)
W zbiorze wartości funkcji f(x)=-2(x+2)^2-1 zawarty
jest przedział:
Odpowiedzi:
| A. (-1,0) | B. (-2,0) |
| C. (-1,+\infty) | D. (-\infty,-1) |
| Zadanie 33. 1 pkt ⋅ Numer: pp-11074 ⋅ Poprawnie: 94/159 [59%] | Rozwiąż |
Podpunkt 33.1 (1 pkt)
« Różnica iloczynu liczby 7 oraz liczby x i kwadratu liczby
xjest największa dla liczby x równej:
Odpowiedź:
| x= | |
| Zadanie 34. 1 pkt ⋅ Numer: pp-11073 ⋅ Poprawnie: 184/339 [54%] | Rozwiąż |
Podpunkt 34.1 (1 pkt)
Dana jest funkcja kwadratowa f(x)=x^2+bx+c, przy czym
f(-2)=f(3)=3.
Wyznacz współczynnik b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 35. 1 pkt ⋅ Numer: pp-11082 ⋅ Poprawnie: 135/246 [54%] | Rozwiąż |
Podpunkt 35.1 (1 pkt)
» W przedziale \langle -1,2\rangle funkcja
y=2x^2+2x-1 osiąga wartość najmniejszą
równą ......... .
Podaj brakującą liczbę.
Odpowiedź:
| y_{min}= | |
| Zadanie 36. 1 pkt ⋅ Numer: pp-11083 ⋅ Poprawnie: 84/187 [44%] | Rozwiąż |
Podpunkt 36.1 (1 pkt)
» Dla x=-2 funkcja
f(x)=x^2+bx+c przyjmuje wartość najmniejszą równą
-6.
Wyznacz wartość współczynnika c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 37. 1 pkt ⋅ Numer: pp-11084 ⋅ Poprawnie: 115/172 [66%] | Rozwiąż |
Podpunkt 37.1 (1 pkt)
Dana jest funkcja y=x^2-6.
Do zbioru ZW_f nie należy liczba:
Odpowiedzi:
| A. 4-5\sqrt{5} | B. 4-3\sqrt{6} |
| C. 5-6\sqrt{3} | D. 5-4\sqrt{5} |
| Zadanie 38. 1 pkt ⋅ Numer: pp-11408 ⋅ Poprawnie: 170/221 [76%] | Rozwiąż |
Podpunkt 38.1 (1 pkt)
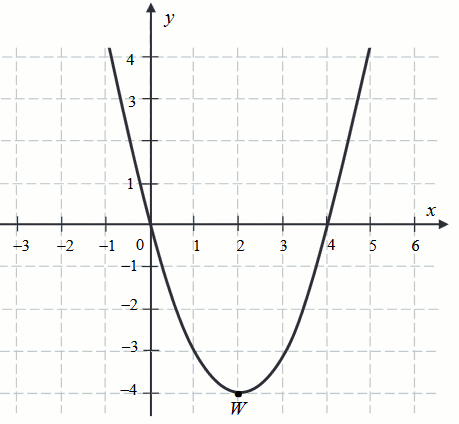
Na rysunku przedstawiono wykres funkcji kwadratowej f:
Zbiór wartości funkcji określonej wzorem y=-f(x) jest równy:
Odpowiedzi:
| A. (-\infty,+\infty) | B. (-\infty, 4\rangle |
| C. \langle -4,0\rangle | D. \langle 4,+\infty) |
| Zadanie 39. 1 pkt ⋅ Numer: pp-10997 ⋅ Poprawnie: 199/271 [73%] | Rozwiąż |
Podpunkt 39.1 (1 pkt)
Wskaż funkcję, która nie przyjmuje wartości ujemnych:
Odpowiedzi:
| A. y=3(x-7)^2-4 | B. y=(6-x)^2+7 |
| C. y=(x+5)^2-7 | D. y=-1(x+1)^2+7 |
| Zadanie 40. 1 pkt ⋅ Numer: pp-11505 ⋅ Poprawnie: 441/844 [52%] | Rozwiąż |
Podpunkt 40.1 (1 pkt)
(1 pkt)
Zbiorem wartości funkcji określonej wzorem
f(x)=-5(x+2011)^2+m-10
jest przedział (-\infty, 2021\rangle.
Wówczas liczba m jest równa:
Odpowiedzi:
| A. 2001 | B. 2011 |
| C. 2031 | D. 2041 |
| Zadanie 41. 1 pkt ⋅ Numer: pp-11813 ⋅ Poprawnie: 680/805 [84%] | Rozwiąż |
Podpunkt 41.1 (1 pkt)
Funkcja kwadratowa f jest określona wzorem
f(x)=(x-2)^2-16.
Jednym z miejsc zerowych tej funkcji jest liczba -2.
Drugim miejscem zerowym funkcji f jest liczba:
Odpowiedzi:
| A. 10 | B. 4 |
| C. 7 | D. 5 |
| E. 9 | F. 8 |
| G. 6 | H. 2 |
| Zadanie 42. 1 pkt ⋅ Numer: pp-11864 ⋅ Poprawnie: 347/471 [73%] | Rozwiąż |
Podpunkt 42.1 (1 pkt)
Wykresem funkcji kwadratowej f(x)=3x^2+bx+c jest parabola o wierzchołku
w punkcie W=(-2,-6). Wzór tej funkcji w postaci kanonicznej to:
Odpowiedzi:
| A. f(x)=3(x+6)^2-2 | B. f(x)=3(x+2)^2-6 |
| C. f(x)=3(x-2)^2+6 | D. f(x)=3(x-6)^2-2 |
| E. f(x)=3(x-2)^2-6 | F. f(x)=3(x+2)^2+6 |
| Zadanie 43. 1 pkt ⋅ Numer: pp-11889 ⋅ Poprawnie: 204/268 [76%] | Rozwiąż |
Podpunkt 43.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=-(x-2)^2-1 jest rosnąca w przedziale:
Odpowiedzi:
| A. \langle -2,+\infty\rangle | B. \langle 2,+\infty\rangle |
| C. (-\infty, -2\rangle | D. (-\infty, 2\rangle |
| Zadanie 44. 2 pkt ⋅ Numer: pp-20336 ⋅ Poprawnie: 86/239 [35%] | Rozwiąż |
Podpunkt 44.1 (1 pkt)
» Punkt P=(-2,0) jest wierzchołkiem paraboli określonej
równaniem y=2x^2+4px+q-2.
Oblicz wartości współczynników p i
q.
Podaj wartość p.
Odpowiedź:
p=
(wpisz liczbę całkowitą)
Podpunkt 44.2 (1 pkt)
Podaj wartość q.
Odpowiedź:
q=
(wpisz liczbę całkowitą)
| Zadanie 45. 2 pkt ⋅ Numer: pp-20337 ⋅ Poprawnie: 180/299 [60%] | Rozwiąż |
Podpunkt 45.1 (2 pkt)
Dana jest funkcja f(x)=a(x+1)^2-4, do wykresu której
nalezy punkt P=(-3,-24).
Wyznacz a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 46. 2 pkt ⋅ Numer: pp-20338 ⋅ Poprawnie: 96/229 [41%] | Rozwiąż |
Podpunkt 46.1 (1 pkt)
» Prosta x=2 jest osią symetrii paraboli
f(x)=ax^2+bx+1, a najmniejsza wartość funkcji
f jest równa -7.
Wyznacz równanie tej funkcji w postaci ogólnej.
Podaj a.
Odpowiedź:
| a= | |
Podpunkt 46.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 47. 2 pkt ⋅ Numer: pp-20339 ⋅ Poprawnie: 76/172 [44%] | Rozwiąż |
Podpunkt 47.1 (1 pkt)
« Najmniejszą wartość równą -26 trójmian
y=x^2+bx+c osiąga dla x=5.
Oblicz b.
Odpowiedź:
| b= | |
Podpunkt 47.2 (1 pkt)
Oblicz c.
Odpowiedź:
| c= | |
| Zadanie 48. 2 pkt ⋅ Numer: pp-20340 ⋅ Poprawnie: 81/206 [39%] | Rozwiąż |
Podpunkt 48.1 (2 pkt)
Współrzędna y wierzchołka wykresu funkcji
f(x)=ax^2+2x-1 jest równa 1.
Wyznacz a.
Odpowiedź:
| a= | |
| Zadanie 49. 2 pkt ⋅ Numer: pp-20341 ⋅ Poprawnie: 257/523 [49%] | Rozwiąż |
Podpunkt 49.1 (2 pkt)
Największa wartość funkcji f(x)=a(x-3)(x+1) jest równa
32.
Podaj a.
Odpowiedź:
| a= | |
| Zadanie 50. 2 pkt ⋅ Numer: pp-20342 ⋅ Poprawnie: 75/123 [60%] | Rozwiąż |
Podpunkt 50.1 (2 pkt)
» Wykres funkcji f(x)=x^2-6x+c-15 jest styczny do osi
Ox.
Wyznacz c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 51. 2 pkt ⋅ Numer: pp-20343 ⋅ Poprawnie: 36/110 [32%] | Rozwiąż |
Podpunkt 51.1 (1 pkt)
« Dane jest funkcja f(x)=-x^2+6x+16, gdzie
x\in\langle 2,8\rangle. Wyznacz
ZW_f.
Zapisz ZW_f w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
y_l=
(wpisz liczbę całkowitą)
Podpunkt 51.2 (1 pkt)
Podaj prawy koniec tego przedziału.
Odpowiedź:
y_p=
(wpisz liczbę całkowitą)
| Zadanie 52. 2 pkt ⋅ Numer: pp-20344 ⋅ Poprawnie: 27/69 [39%] | Rozwiąż |
Podpunkt 52.1 (1 pkt)
» Zbiorem wartości funkcji kwadratowej f jest przedział
(-\infty,27\rangle oraz
f(x) > 0\iff x\in(-2,4).
Wyznacz wzór funkcji f(x)=ax^2+bx+c i podaj wartość współczynnika a tej funkcji.
Odpowiedź:
| a= | |
Podpunkt 52.2 (1 pkt)
Podaj sumę obu współrzędnych wierzchołka tej paraboli.
Odpowiedź:
| x_w+y_w= | |
| Zadanie 53. 3 pkt ⋅ Numer: pp-20841 ⋅ Poprawnie: 60/101 [59%] | Rozwiąż |
Podpunkt 53.1 (2 pkt)
» Wyznacz współczynniki b i c
funkcji określonej wzorem f(x)=2x^2+bx+c wiedząc, że zbiorem jej wartości
jest przedział \langle -2,+\infty), a osią symetrii jej
wykresu jest prosta x=2.
Podaj b.
Odpowiedź:
| b= | |
Podpunkt 53.2 (1 pkt)
Podaj c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 54. 2 pkt ⋅ Numer: pp-21057 ⋅ Poprawnie: 306/751 [40%] | Rozwiąż |
Podpunkt 54.1 (2 pkt)
Oceń, które podanych funkcji mają zbiór wartości będący przedziałem
(-\infty, 3]:
Odpowiedzi:
| T/N : f(x)=(x-3)^2 | T/N : f(x)=2x^2+3 |
| T/N : f(x)=-2(x-4)^2 | T/N : f(x)=x^2-x+4 |
| Zadanie 55. 2 pkt ⋅ Numer: pp-21073 ⋅ Poprawnie: 75/163 [46%] | Rozwiąż |
Podpunkt 55.1 (1 pkt)
Funkcja kwadratowa f określona wzorem f(x)=ax^2+bx+c ma dokładnie jedno miejsce
zerowe równe -1. Ponadto f(0)=4.
Wyznacz współczynnik a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 55.2 (1 pkt)
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 56. 4 pkt ⋅ Numer: pp-30060 ⋅ Poprawnie: 32/66 [48%] | Rozwiąż |
Podpunkt 56.1 (2 pkt)
« Zbiorem wartości funkcji kwadratowej jest przedział
(-\infty,c\rangle oraz
f(x_1)=f(x_2)=d.
Zapisz wzór tej funkcji w postaci ogólnej. Podaj najmniejszy współczynnik występujący w tym wzorze.
Dane
c=-2
x1=0
x2=2
d=-5
x1=0
x2=2
d=-5
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 56.2 (2 pkt)
Podaj największy współczynnik występujący w tym wzorze.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 57. 4 pkt ⋅ Numer: pp-30061 ⋅ Poprawnie: 40/96 [41%] | Rozwiąż |
Podpunkt 57.1 (2 pkt)
« Dana jest funkcja kwadratowa f(x)=ax^2+bx+c, która
spełnia warunek f(x_1)=f(x_2)=y_1.
Najmniejszą wartością funkcji f jest liczba
y_2.
Oblicz wartość współczynnika a.
Dane
x_1=-4
x_2=0
y_1=-24
y_2=-32
x_2=0
y_1=-24
y_2=-32
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 57.2 (2 pkt)
Oblicz wartość współczynnika b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 58. 4 pkt ⋅ Numer: pp-30062 ⋅ Poprawnie: 27/134 [20%] | Rozwiąż |
Podpunkt 58.1 (2 pkt)
« Wyznacz współczynniki p i
q funkcji g(x)=ax^2+px+q
wiedząc, że ZW_f=\langle m,+\infty) oraz
g(0)=n.
Podaj p^2.
Dane
a=2
m=-2
n=6
m=-2
n=6
Odpowiedź:
p^2=
(wpisz liczbę całkowitą)
Podpunkt 58.2 (2 pkt)
Podaj q.
Odpowiedź:
q=
(wpisz liczbę całkowitą)
| Zadanie 59. 4 pkt ⋅ Numer: pp-30068 ⋅ Poprawnie: 32/124 [25%] | Rozwiąż |
Podpunkt 59.1 (2 pkt)
Dana jest funkcja g(x)=x^2+4px+1, która
spełnia warunek ZW_{g}=\langle a,+\infty).
Wyznacz p.
Podaj najmniejsze możliwe p.
Dane
a=-13
Odpowiedź:
| p_{min}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 59.2 (2 pkt)
Podaj największe możliwe p.
Odpowiedź:
| p_{max}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 60. 4 pkt ⋅ Numer: pp-30064 ⋅ Poprawnie: 143/371 [38%] | Rozwiąż |
Podpunkt 60.1 (2 pkt)
» Wyznacz współczynniki b i
c funkcji
f(x)=-\frac{1}{a}x^2+bx+c wiedząc, że
jej jedynym miejscem zerowym jest liczba p.
Podaj b.
Dane
a=3
p=-12
p=-12
Odpowiedź:
| b= | |
Podpunkt 60.2 (2 pkt)
Podaj c.
Odpowiedź:
| c= | |
| Zadanie 61. 4 pkt ⋅ Numer: pp-30065 ⋅ Poprawnie: 5/40 [12%] | Rozwiąż |
Podpunkt 61.1 (2 pkt)
» Punkt O=(0,0) należy do wykresu funkcji
kwadratowej y=g(x). Funkcja
h(x)=g(x+1) przyjmuje wartość największą równą
m dla x=n.
Wyznacz wzory obu funkcji w postaci ogólnej.
Podaj sumę współczynników funkcji g.
Dane
m=5
n=2
n=2
Odpowiedź:
| \frac{a}{b}= | |
Podpunkt 61.2 (2 pkt)
Podaj sumę współczynników h.
Odpowiedź:
| \frac{a}{b}= | |
| Zadanie 62. 4 pkt ⋅ Numer: pp-30066 ⋅ Poprawnie: 48/107 [44%] | Rozwiąż |
Podpunkt 62.1 (2 pkt)
« Wierzchołek wykresu funkcji kwadratowej
f(x)=ax^2-12x+11, gdzie a > 0, należy do
prostej o równaniu y=-1. Oblicz współrzędne tego wierzchołka.
Podaj odciętą wierzchołka paraboli.
Odpowiedź:
x_w=
(wpisz liczbę całkowitą)
Podpunkt 62.2 (2 pkt)
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 63. 4 pkt ⋅ Numer: pp-30067 ⋅ Poprawnie: 44/177 [24%] | Rozwiąż |
Podpunkt 63.1 (1 pkt)
» Funkcja kwadratowa f(x)=ax^2+bx-6 jest
malejąca w przedziale (-\infty,-1\rangle, a rosnąca
w przedziale \langle -1,+\infty). Wierzchołek
paraboli będącej wykresem tej funkcji należy do prostej o równaniu
y=3x-5.
Zapisz wzór tej funkcji w postaci kanonicznej y=a(x-p)^2+q. Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 63.2 (1 pkt)
Podaj q.
Odpowiedź:
q=
(wpisz liczbę całkowitą)
Podpunkt 63.3 (2 pkt)
Wyznacz miejsca zerowe tej funkcji.
Podaj mniejsze z miejsc zerowych.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)