Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Najmniejsza i największa wartość funkcji kwadratowej w przedziale

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-11466 ⋅ Poprawnie: 204/339 [60%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 « Dana jest funkcja kwadratowa f(x)=-0,5(x+2m)^2+10m, gdzie m > 0.

Wówczas:

Odpowiedzi:
A. dla m=-\frac{1}{2} funkcja jest rosnąca B. największą wartością funkcji jest -10m
C. wierzchołek paraboli, która jest wykresem tej funkcji należy do prostej y=-5x D. dla pewnego m funkcja ma jedno miejsce zerowe
Zadanie 2.  1 pkt ⋅ Numer: pp-11465 ⋅ Poprawnie: 481/946 [50%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 » Najmniejszą wartość w przedziale \langle 8, 12\rangle funkcja kwadratowa f(x)=-\left(x-9\right)^{2}-5 przyjmuje dla argumentu ......... .

Podaj brakującą liczbę.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 3.  1 pkt ⋅ Numer: pp-10978 ⋅ Poprawnie: 475/746 [63%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 « Najmniejszą wartość w przedziale \langle -12, -8\rangle funkcja kwadratowa określona wzorem f(x)=-\left(x+9\right)^{2}+5 przyjmuje dla argumentu ......... .

Podaj brakującą liczbę.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 4.  1 pkt ⋅ Numer: pp-10985 ⋅ Poprawnie: 233/345 [67%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 Dana jest funkcja g(x)=-\frac{1}{4}(x+6)x, gdzie x\in\langle -10,-7\rangle.

Wyznacz f_{min}.

Odpowiedź:
f_{min}=
(wpisz dwie liczby całkowite)
Zadanie 5.  1 pkt ⋅ Numer: pp-11409 ⋅ Poprawnie: 223/340 [65%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
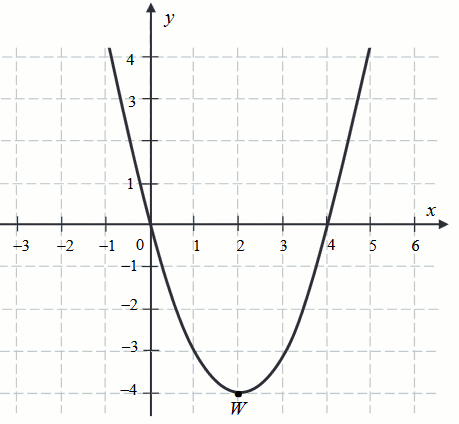
Na rysunku przedstawiono wykres funkcji kwadratowej f:

Podaj największą wartość funkcji f w przedziale \langle 1,4\rangle.

Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 6.  1 pkt ⋅ Numer: pp-10988 ⋅ Poprawnie: 72/95 [75%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
» Wyznacz najmniejszą wartość funkcji kwadratowej określonej wzorem f(x)=x^2+12x.
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Zadanie 7.  2 pkt ⋅ Numer: pp-20353 ⋅ Poprawnie: 223/691 [32%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 « Funkcja kwadratowa jest określona wzorem f(x)=ax^2+bx+c.

Oblicz najmniejszą wartość funkcji f w przedziale \langle p,q\rangle.

Dane
a=-1
b=-7
c=8
p=-7
q=3
Odpowiedź:
y_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 7.2 (1 pkt)
 Oblicz największą wartość funkcji f w tym przedziale.
Odpowiedź:
y_{max}=
(wpisz dwie liczby całkowite)
Zadanie 8.  2 pkt ⋅ Numer: pp-20361 ⋅ Poprawnie: 166/430 [38%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 Dana jest funkcja f(x)=ax^2+bx+c, gdzie x\in\langle p,q\rangle.

Oblicz najmniejszą wartość funkcji f.

Dane
a=1
b=10
c=-10
p=-7
q=-2
Odpowiedź:
y_{min}=
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (1 pkt)
 Oblicz największą wartość funkcji f.
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 9.  2 pkt ⋅ Numer: pp-20362 ⋅ Poprawnie: 18/49 [36%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Dana jest funkcja f(x)=ax^2+bx+c. Wyznacz zbiór wartości funkcji g(x)=f(x-p)+q.

Podaj najmniejszą liczbę w zbiorze wartości. Jeśli taka wartość nie istnieje wpisz 0.

Dane
a=-1
b=6
c=9
p=3
q=-4
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
 Podaj największą liczbę w zbiorze wartości. Jeśli taka wartość nie istnieje wpisz 0.
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 10.  2 pkt ⋅ Numer: pp-20363 ⋅ Poprawnie: 175/370 [47%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 « Dana jest funkcja f(x)=x^2+bx+c, gdzie x\in\langle p, q\rangle.

Oblicz najmniejszą wartość funkcji f.

Dane
b=6
c=12
p=-6
q=-4
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
 Oblicz największą wartość funkcji f.
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 11.  2 pkt ⋅ Numer: pp-20364 ⋅ Poprawnie: 114/261 [43%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 « Wyznacz najmniejszą wartość funkcji h(x)=ax^2+bx+c w przedziale \langle p,q\rangle.
Dane
a=-1
b=6
c=-7
p=1
q=7
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
 Wyznacz największą wartość tej funkcji w podanym przedziale.
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 12.  2 pkt ⋅ Numer: pp-20365 ⋅ Poprawnie: 84/186 [45%] Rozwiąż 
Podpunkt 12.1 (2 pkt)
 « Dana jest funkcja f(x)=ax^2+bx+c.

Oblicz najmniejszą wartość funkcji f w przedziale \langle p, q\rangle.

Dane
a=-1
b=6
c=-7
p=1
q=7
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Zadanie 13.  2 pkt ⋅ Numer: pp-20366 ⋅ Poprawnie: 64/115 [55%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 Funkcja kwadratowa jest określona wzorem f(x)=ax^2+bx+c.

Oblicz najmniejszą wartość funkcji f w przedziale \langle p,q\rangle.

Dane
a=1
b=-6
c=11
p=1
q=7
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
 Dla jakiego x funkcja f osiąga minimum?
Odpowiedź:
x= (wpisz liczbę całkowitą)
Zadanie 14.  2 pkt ⋅ Numer: pp-20367 ⋅ Poprawnie: 9/36 [25%] Rozwiąż 
Podpunkt 14.1 (2 pkt)
 Do wykresu paraboli y=2x^2-3x-1 należy punkt Q=(2am, y) taki, że różnica 2am-y jest największa z możliwych.

Podaj m.

Dane
a=\frac{1}{2}=0.50000000000000
Odpowiedź:
m=
(wpisz dwie liczby całkowite)
Zadanie 15.  2 pkt ⋅ Numer: pp-20368 ⋅ Poprawnie: 47/107 [43%] Rozwiąż 
Podpunkt 15.1 (1 pkt)
 » Wyznacz najmniejszą wartość funkcji g(x)=ax^2+bx+c w przedziale \langle p,q\rangle.
Dane
a=-1
b=6
c=-7
p=4
q=8
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
 Wyznacz największą wartość tej funkcji w podanym przedziale.
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 16.  2 pkt ⋅ Numer: pp-20354 ⋅ Poprawnie: 76/129 [58%] Rozwiąż 
Podpunkt 16.1 (1 pkt)
 «« Dana jest funkcja f(x)=ax^2+bx+c. Oblicz najmniejszą i największą wartość tej funkcji w przedziale \langle p,q\rangle.

Podaj wartośc najmniejszą.

Dane
a=-2
b=12
c=-16
p=4
q=8
Odpowiedź:
f_{min}(x)= (wpisz liczbę całkowitą)
Podpunkt 16.2 (1 pkt)
 Podaj wartośc największą.
Odpowiedź:
f_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 17.  2 pkt ⋅ Numer: pp-20355 ⋅ Poprawnie: 22/83 [26%] Rozwiąż 
Podpunkt 17.1 (1 pkt)
 Dana jest funkcja f(x)=ax^2+bx+c. Oblicz najmniejszą i największą wartość tej funkcji w przedziale \langle p,q\rangle.

Podaj wartośc najmniejszą.

Dane
a=-1
b=-\frac{2}{3}=-0.66666666666667
c=\frac{17}{9}=1.88888888888889
p=-3
q=3
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 17.2 (1 pkt)
 Podaj wartośc największą.
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 18.  2 pkt ⋅ Numer: pp-20356 ⋅ Poprawnie: 25/92 [27%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
 Dana jest funkcja f(x)=ax^2+bx+c. Oblicz najmniejszą i największą wartość tej funkcji w przedziale \langle p,q\rangle.

Podaj wartośc najmniejszą.

Dane
a=-2
b=12
c=-\frac{53}{3}=-17.66666666666670
p=1
q=6
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 18.2 (1 pkt)
 Podaj wartośc największą.
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 19.  2 pkt ⋅ Numer: pp-20357 ⋅ Poprawnie: 15/54 [27%] Rozwiąż 
Podpunkt 19.1 (1 pkt)
 « Dana jest funkcja f(x)=ax^2+bx+c. Oblicz najmniejszą i największą wartość tej funkcji w przedziale \langle p,q\rangle.

Podaj wartośc najmniejszą.

Dane
a=-1
b=-\frac{2}{5}=-0.40000000000000
c=\frac{62}{21}=2.96000000000000
p=-3
q=3
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 19.2 (1 pkt)
 Podaj wartośc największą.
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 20.  2 pkt ⋅ Numer: pp-20358 ⋅ Poprawnie: 32/67 [47%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
 « Dana jest funkcja f(x)=ax^2+bx+c. Oblicz najmniejszą i największą wartość tej funkcji w przedziale \langle p,q\rangle.

Podaj wartośc najmniejszą.

Dane
a=-2
b=-\frac{4}{5}=-0.80000000000000
c=\frac{38}{13}=2.92000000000000
p=-3
q=3
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 20.2 (1 pkt)
 Podaj wartośc największą.
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 21.  2 pkt ⋅ Numer: pp-20359 ⋅ Poprawnie: 53/113 [46%] Rozwiąż 
Podpunkt 21.1 (2 pkt)
 » Wyznacz największą wartość funkcji f(x)=bx+ax^2.
Dane
a=-\frac{2}{3}=-0.66666666666667
b=\frac{3}{5}=0.60000000000000
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 22.  2 pkt ⋅ Numer: pp-20360 ⋅ Poprawnie: 21/52 [40%] Rozwiąż 
Podpunkt 22.1 (2 pkt)
 » Wyznacz najmniejszą wartość funkcji f(x)=bx+ax^2.
Dane
a=\frac{2}{3}=0.66666666666667
b=-\frac{3}{2}=-1.50000000000000
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Zadanie 23.  4 pkt ⋅ Numer: pp-30078 ⋅ Poprawnie: 37/121 [30%] Rozwiąż 
Podpunkt 23.1 (2 pkt)
 Dana jest funkcja f(x)=(ax+b)(cx+d). Oblicz najmniejszą i największą wartość tej funkcji w przedziale \langle p,q\rangle.

Podaj wartość najmniejszą w tym przedziale.

Dane
a=-1
b=1
c=-3
d=6
p=-4
q=6
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 23.2 (2 pkt)
 Podaj wartość największą w tym przedziale.
Odpowiedź:
max=
(wpisz dwie liczby całkowite)
Zadanie 24.  4 pkt ⋅ Numer: pp-30079 ⋅ Poprawnie: 22/92 [23%] Rozwiąż 
Podpunkt 24.1 (2 pkt)
 « Liczba c jest rozwiązaniem równania 8^{p}+2^{q}\cdot x=0, zaś liczba d wynosi \frac{125^{500}}{5^{1500}}. Funkcja kwadratowa g(x)=(x-c)(x-d) określona jest w przedziale \langle x_1,x_2\rangle.

Podaj najmniejszą wartość funkcji g.

Dane
p=12
q=33
x1=-6
x2=1
Odpowiedź:
min=
(wpisz dwie liczby całkowite)
Podpunkt 24.2 (2 pkt)
 Podaj największą wartość funkcji g.
Odpowiedź:
g_{max}(x)= (wpisz liczbę całkowitą)
Zadanie 25.  4 pkt ⋅ Numer: pp-30080 ⋅ Poprawnie: 43/114 [37%] Rozwiąż 
Podpunkt 25.1 (4 pkt)
» Największa wartość funkcji kwadratowej f(x)=a(x-5)^2-6 w przedziale \langle -1,1\rangle jest równa 10. Wyznacz najmniejszą wartość funkcji f w przedziale \langle -1,1\rangle.

Podaj tę wartość.

Odpowiedź:
y_{min}=
(wpisz dwie liczby całkowite)
Zadanie 26.  4 pkt ⋅ Numer: pp-30081 ⋅ Poprawnie: 14/46 [30%] Rozwiąż 
Podpunkt 26.1 (4 pkt)
 « Dana jest funkcja kwadratowa h(x)=-\frac{1}{2}x^2-x+7,5 określona w przedziale w przedziale \langle -2, m+a\rangle. Funkcja h spełnia warunek h_{max}-h_{min}=\frac{9}{2}.

Oblicz m.

Dane
a=2
Odpowiedź:
m= (wpisz liczbę całkowitą)
Zadanie 27.  4 pkt ⋅ Numer: pp-30082 ⋅ Poprawnie: 29/61 [47%] Rozwiąż 
Podpunkt 27.1 (4 pkt)
 «« Wyznacz wartość największą funkcji f(x)=\frac{1}{x^2+12x+31} w przedziale \langle a,b\rangle.

Podaj tę wartość.

Dane
a=-3
b=1
Odpowiedź:
y_{max}=
(wpisz dwie liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm