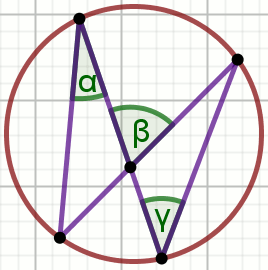
Kąty i koła
Zadania dla liceum ogólnokształcącego - poziom podstawowy
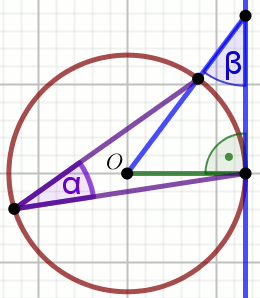
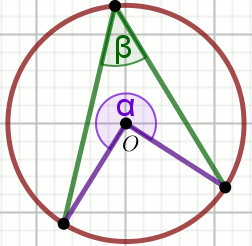
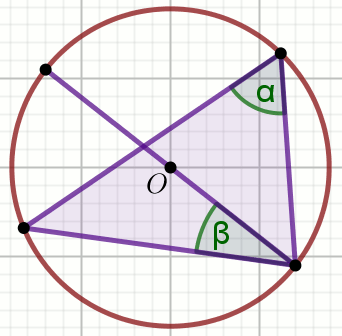
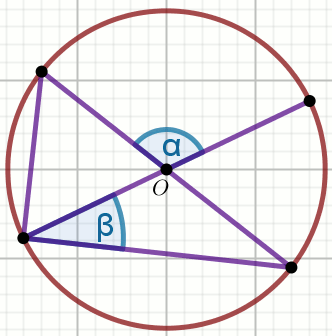
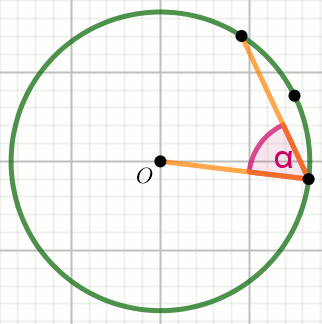
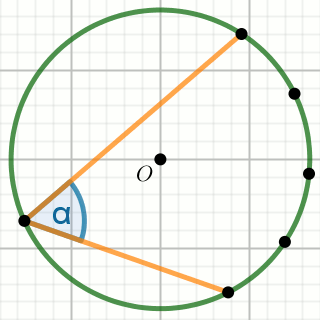
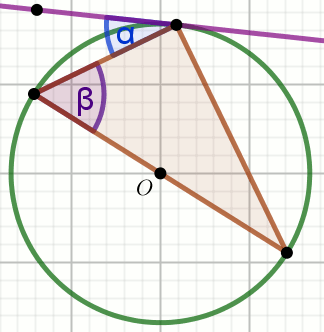
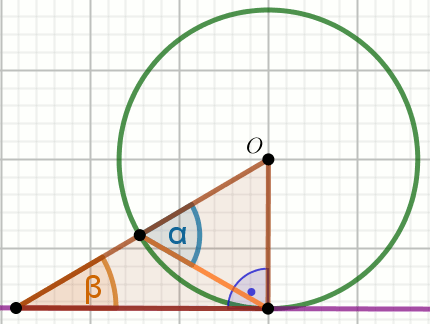
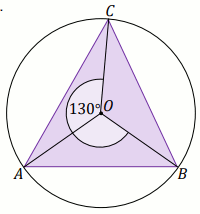
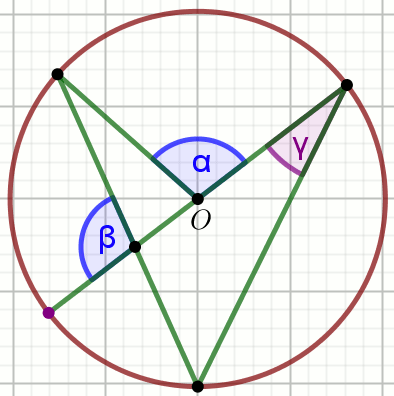
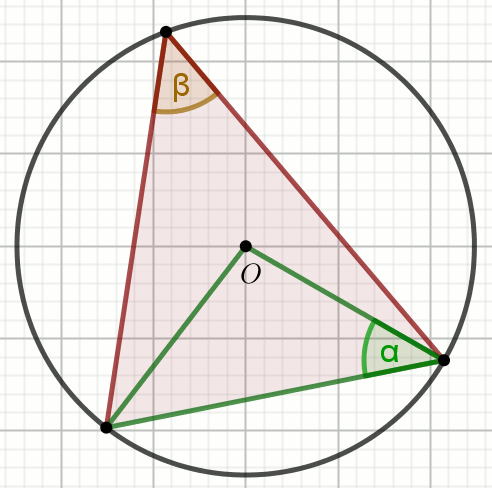
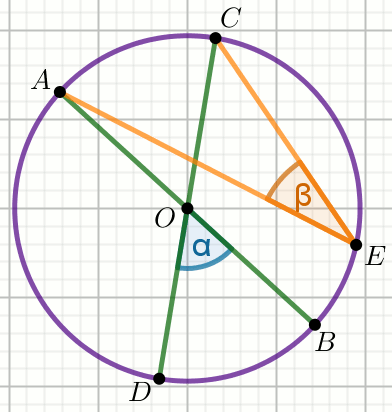
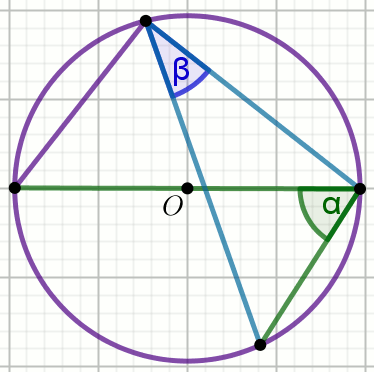
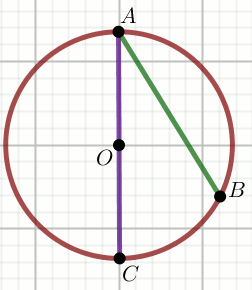
kąt środkowy
kąt wpisany w okrąg
kąty oparte na łuku
kąty w okręgu
kąt dopisany do okręgu
łuk okręgu
cięciwa okręgu
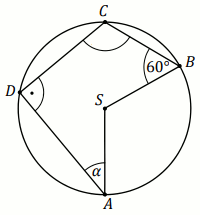
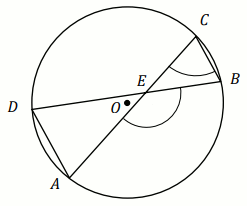
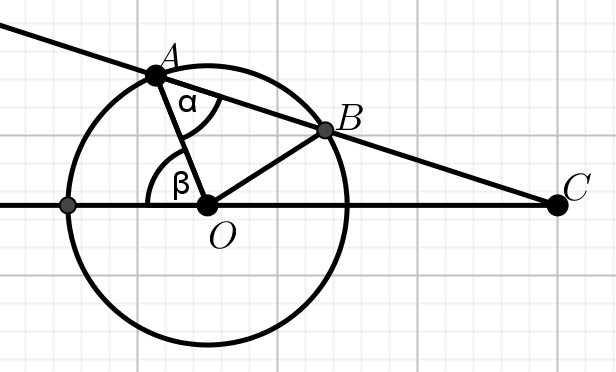
Zadanie 1. 1 pkt ⋅ Numer: pp-10546 ⋅ Poprawnie: 630/964 [65%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
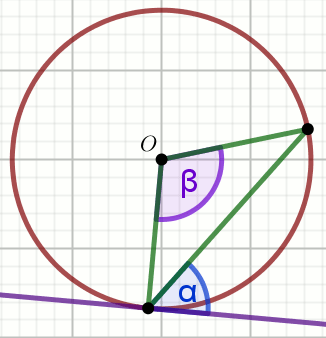
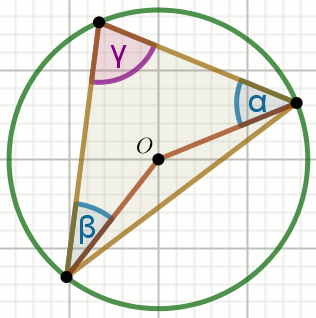
Punkt
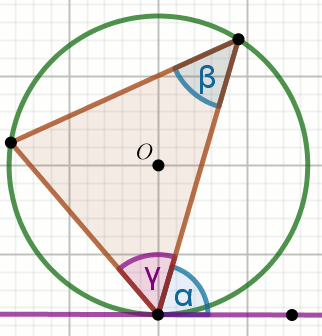
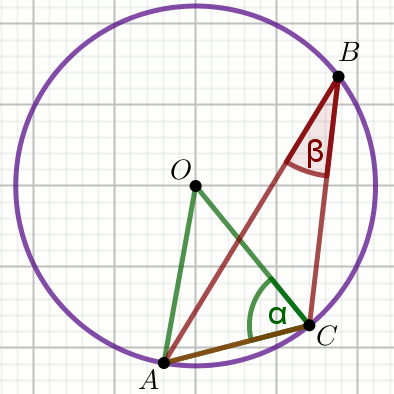
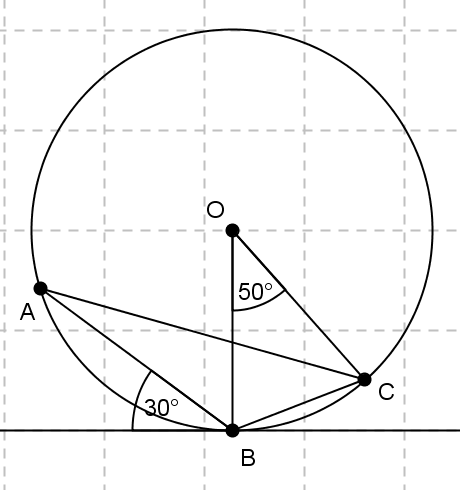
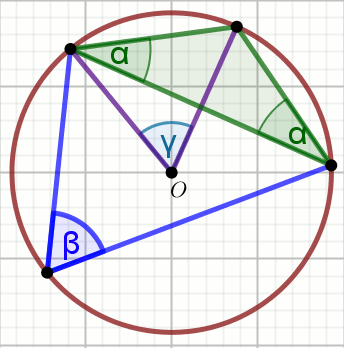
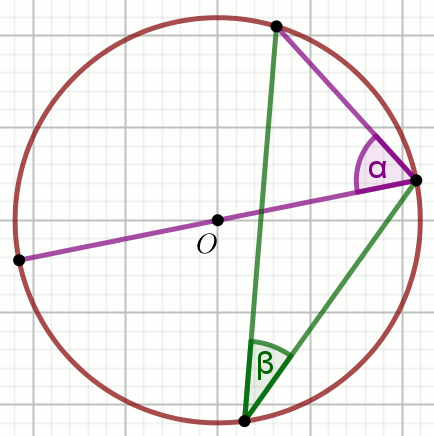
O jest środkiem okręgu na rysunku, w którym
\alpha=34^{\circ} :
Wyznacz miary stopniowe kątów \beta i
\gamma .
Odpowiedzi:
Zadanie 2. 1 pkt ⋅ Numer: pp-10494 ⋅ Poprawnie: 199/447 [44%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
« Punkt
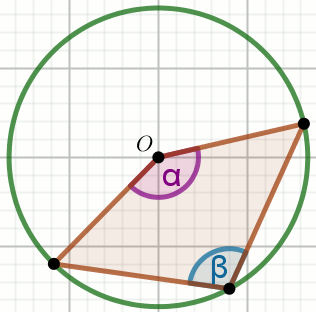
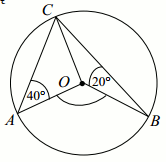
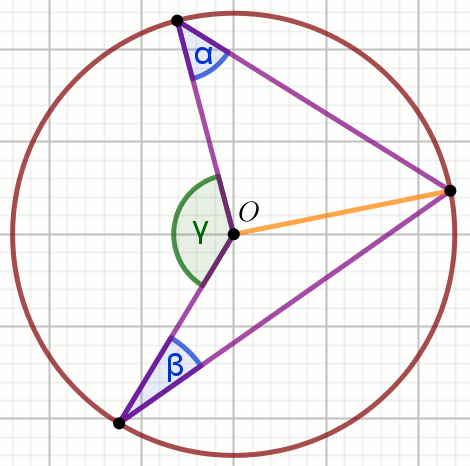
O jest środkiem okręgu na rysunku,
w którym
\alpha=40^{\circ} :
Wyznacz miary stopniowe kątów \beta i \gamma .
Odpowiedzi:
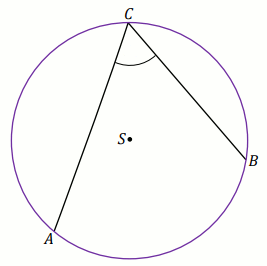
Zadanie 3. 1 pkt ⋅ Numer: pp-10504 ⋅ Poprawnie: 722/1039 [69%]
Rozwiąż
Podpunkt 3.1 (1 pkt)
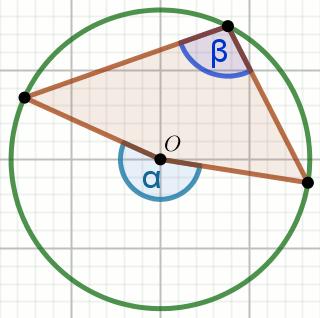
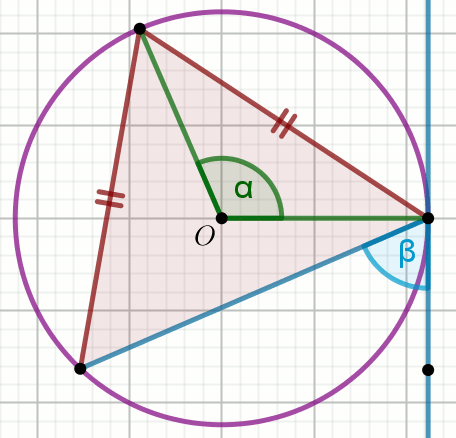
Punkt
O jest środkiem okręgu, w którym
\alpha=33^{\circ} :
Oblicz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
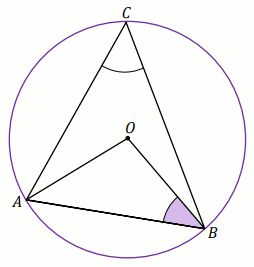
Zadanie 4. 1 pkt ⋅ Numer: pp-10544 ⋅ Poprawnie: 294/481 [61%]
Rozwiąż
Podpunkt 4.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, w którym
\alpha=100^{\circ} i
\beta=108^{\circ} :
Oblicz miarę stopniową kąta \gamma .
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 5. 1 pkt ⋅ Numer: pp-10526 ⋅ Poprawnie: 189/274 [68%]
Rozwiąż
Podpunkt 5.1 (1 pkt)
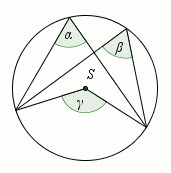
Dany jest okrąg
o(O, r) :
Oblicz miarę stopniową kąta \alpha .
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
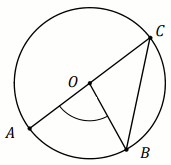
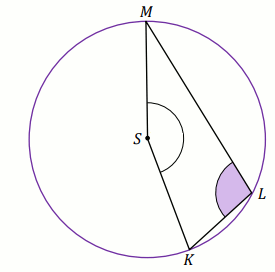
Zadanie 6. 1 pkt ⋅ Numer: pp-10543 ⋅ Poprawnie: 89/124 [71%]
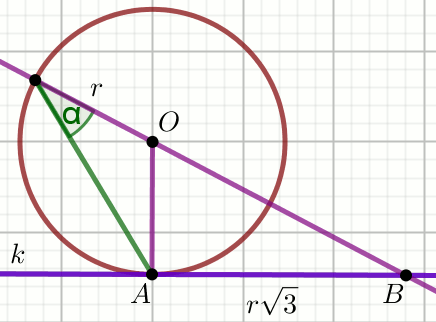
Rozwiąż
Podpunkt 6.1 (1 pkt)
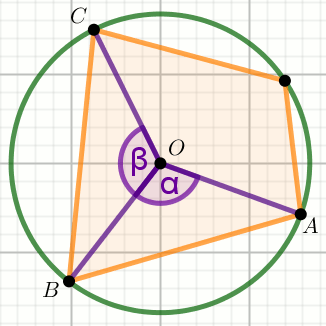
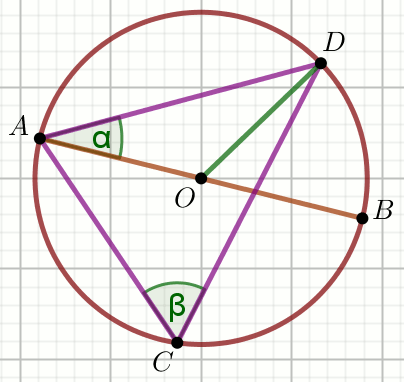
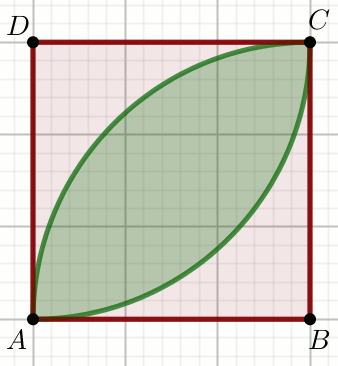
» Czworokąt na rysunku jest kwadratem o boku długości
5\sqrt{2} , a okręgi przechodzące przez punkty
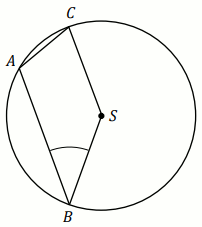
A i
C mają środki w
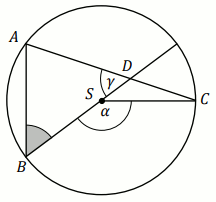
punktach
B i
D :
Oblicz pole powierzchni zielonej figury i zapisz wynik w postaci
m+n\cdot \pi , gdzie m,n\in\mathbb{Z} .
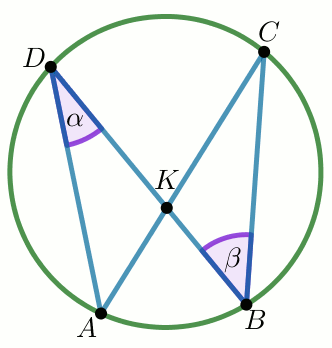
Podaj liczby m i n .
Odpowiedzi:
Zadanie 7. 1 pkt ⋅ Numer: pp-10482 ⋅ Poprawnie: 514/677 [75%]
Rozwiąż
Podpunkt 7.1 (1 pkt)
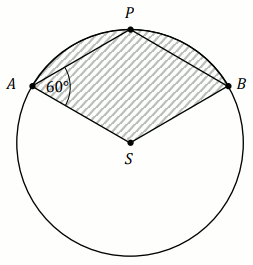
Kąt środkowy okręgu
\alpha i kąt wpisany w ten okrąg są oparte na tym samym łuku.
Suma ich miar jest równa
180^{\circ} .
Jaka jest miara stopniowa kąta środkowego?
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 8. 1 pkt ⋅ Numer: pp-10547 ⋅ Poprawnie: 663/914 [72%]
Rozwiąż
Podpunkt 8.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, w którym
\beta=120^{\circ} i
\gamma=31^{\circ} :
Obicz miarę stopniową kąta \alpha .
Odpowiedź:
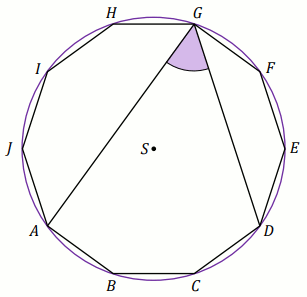
\alpha=
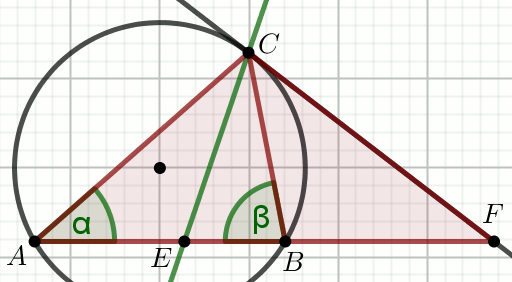
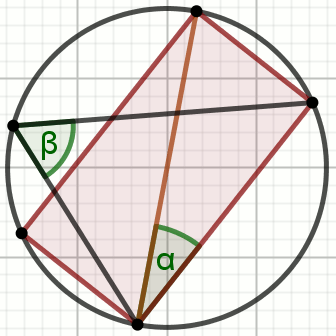
(wpisz liczbę całkowitą)
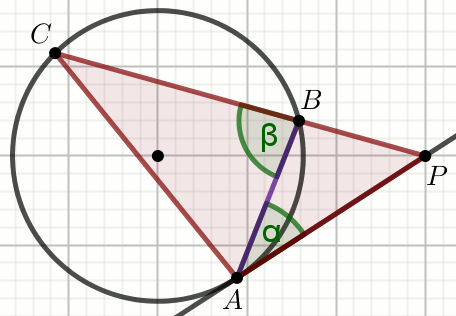
Zadanie 9. 1 pkt ⋅ Numer: pp-10548 ⋅ Poprawnie: 293/561 [52%]
Rozwiąż
Podpunkt 9.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, w którym
\alpha=56^{\circ} :
Oblicz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 10. 1 pkt ⋅ Numer: pp-10483 ⋅ Poprawnie: 174/258 [67%]
Rozwiąż
Podpunkt 10.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, w którym:
\alpha=28^{\circ} i
\beta=46^{\circ} :
Oblicz miarę stopniową kąta \gamma .
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 11. 1 pkt ⋅ Numer: pp-10484 ⋅ Poprawnie: 167/224 [74%]
Rozwiąż
Podpunkt 11.1 (1 pkt)
Oblicz miarę stopniową kąta środkowego opartego na łuku, którego długość jest równa
\frac{2}{9} długości okręgu.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
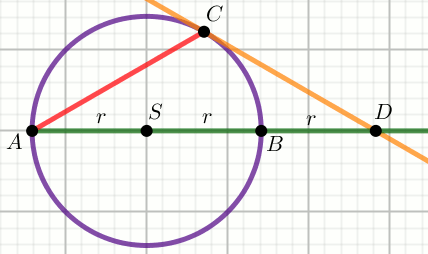
Zadanie 12. 1 pkt ⋅ Numer: pp-10485 ⋅ Poprawnie: 483/727 [66%]
Rozwiąż
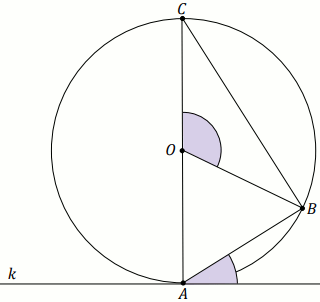
Podpunkt 12.1 (1 pkt)
Punkt
O jest środkiem okręgu opisanego na trojkącie
równoramiennym, a prosta jest styczną do tego okręgu:
Wiedząc, że \alpha=144^{\circ} , wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 13. 1 pkt ⋅ Numer: pp-10486 ⋅ Poprawnie: 314/406 [77%]
Rozwiąż
Podpunkt 13.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku:
Wiedząc, że
\alpha=36^{\circ} , wyznacz miarę stopniową kąta
\beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 14. 1 pkt ⋅ Numer: pp-10542 ⋅ Poprawnie: 78/110 [70%]
Rozwiąż
Podpunkt 14.1 (1 pkt)
Pięć punktów na okręgu dzieli go na łuki o długościach
6 ,
2 ,
3 ,
6 i
x . Kąt środkowy tego okręgu oparty na łuku o długości
6 ma miarę
48^{\circ} .
Oblicz x .
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Zadanie 15. 1 pkt ⋅ Numer: pp-10488 ⋅ Poprawnie: 201/279 [72%]
Rozwiąż
Podpunkt 15.1 (1 pkt)
Punkt
O jest środkiem okręgu o średnicy
AB , w którym
\alpha=106^{\circ} :
Oblicz miarę stopniową kąta \gamma .
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 16. 1 pkt ⋅ Numer: pp-10489 ⋅ Poprawnie: 182/258 [70%]
Rozwiąż
Podpunkt 16.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, w którym
\alpha=60^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 17. 1 pkt ⋅ Numer: pp-10539 ⋅ Poprawnie: 266/387 [68%]
Rozwiąż
Podpunkt 17.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, przy czym
\alpha=53^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 18. 1 pkt ⋅ Numer: pp-10491 ⋅ Poprawnie: 57/76 [75%]
Rozwiąż
Podpunkt 18.1 (1 pkt)
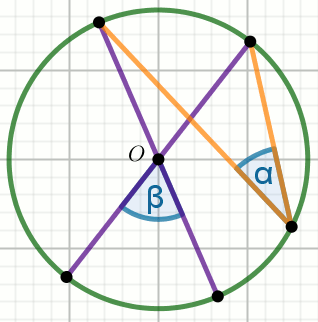
« W kąt
\alpha o mierze
45^{\circ} wpisano okrąg o środku
O styczny do ramion kąta w punktach
A i
B .
Wyznacz miarę stopniową mniejszego z kątów środkowych okręgu AOB .
Odpowiedź:
|\sphericalangle AOB|=
(wpisz liczbę całkowitą)
Zadanie 19. 1 pkt ⋅ Numer: pp-10492 ⋅ Poprawnie: 123/173 [71%]
Rozwiąż
Podpunkt 19.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, w którym:
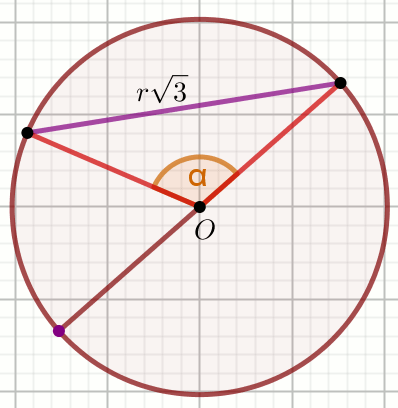
|AO|=9 oraz
|AB|=9\sqrt{3} :
Wówczas:
Odpowiedzi:
A. |\sphericalangle BCA|=45^{\circ}
B. |\sphericalangle BOC|=60^{\circ}
C. |\sphericalangle BCA|=90^{\circ}
D. |\sphericalangle BAC|=45^{\circ}
Zadanie 20. 1 pkt ⋅ Numer: pp-10493 ⋅ Poprawnie: 275/414 [66%]
Rozwiąż
Podpunkt 20.1 (1 pkt)
» Miara kąta wpisanego w okrąg jest o
51^{\circ}
mniejsza od miary kąta środkowego opartego na tym samym łuku.
Oblicz miarę stopniową kąta wpisanego w ten okrąg.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 21. 1 pkt ⋅ Numer: pp-10495 ⋅ Poprawnie: 130/186 [69%]
Rozwiąż
Podpunkt 21.1 (1 pkt)
» Długości przyprostokątnych trójkąta prostokątnego są równe
20 i
48 .
Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka kąta prostego.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 22. 1 pkt ⋅ Numer: pp-10496 ⋅ Poprawnie: 32/89 [35%]
Rozwiąż
Podpunkt 22.1 (1 pkt)
«« Na okręgu o promieniu długości
r zaznaczono
punkty
A i
B , które
wyznaczyły łuk o długości
\frac{\pi}{3}\cdot r .
Wyznacz miarę stopniową kąta wpisanego w ten okrąg opartego na tym łuku.
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 23. 1 pkt ⋅ Numer: pp-10478 ⋅ Poprawnie: 49/76 [64%]
Rozwiąż
Podpunkt 23.1 (1 pkt)
«« Kąt wpisany w okrąg o promieniu
\sqrt{7} ma miarę
20^{\circ} . Długość łuku, na którym oparty jest
ten kąt można zapisać w postaci
a\cdot \sqrt{7}\cdot \pi .
Podaj liczbę a .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 24. 1 pkt ⋅ Numer: pp-10498 ⋅ Poprawnie: 181/282 [64%]
Rozwiąż
Podpunkt 24.1 (1 pkt)
» Punkt
O jest środkiem okręgu na rysunku, przy czym
|OB|=|BC| i
\alpha=46^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 25. 1 pkt ⋅ Numer: pp-10499 ⋅ Poprawnie: 207/295 [70%]
Rozwiąż
Podpunkt 25.1 (1 pkt)
Oblicz miarę stopniową zaznaczonego na rysunku kąta
\gamma wiedząc,
że
\alpha=35^{\circ} i
\beta=52^{\circ} :
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 26. 1 pkt ⋅ Numer: pp-10500 ⋅ Poprawnie: 63/87 [72%]
Rozwiąż
Podpunkt 26.1 (1 pkt)
« Dłuższa przekątna sześciokąta foremnego ma długość
2\sqrt{11} .
Oblicz pole powierzchni tego sześciokąta.
Odpowiedź:
Zadanie 27. 1 pkt ⋅ Numer: pp-10536 ⋅ Poprawnie: 110/152 [72%]
Rozwiąż
Podpunkt 27.1 (1 pkt)
Punkt
O jest środkiem okręgu, przy czym
\beta=40^{\circ} :
Kąt \alpha , zaznaczony na rysunku, ma miarę:
Odpowiedzi:
A. 25^{\circ}
B. 29^{\circ}
C. 28^{\circ}
D. 21^{\circ}
E. 23^{\circ}
F. 31^{\circ}
Zadanie 28. 1 pkt ⋅ Numer: pp-10535 ⋅ Poprawnie: 205/255 [80%]
Rozwiąż
Podpunkt 28.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, przy czym
\alpha=250^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 29. 1 pkt ⋅ Numer: pp-10514 ⋅ Poprawnie: 185/314 [58%]
Rozwiąż
Podpunkt 29.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, przy czym
\beta=26^{\circ} :
Wyznacz miarę stopniową zaznaczonego na rysunku kąta \alpha .
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 30. 1 pkt ⋅ Numer: pp-10505 ⋅ Poprawnie: 178/231 [77%]
Rozwiąż
Podpunkt 30.1 (1 pkt)
Punkt
O na rysunku jest środkiem okręgu, przy czym
\alpha=50^{\circ} :
Wyznacz miarę zaznaczonego na rysunku kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 31. 1 pkt ⋅ Numer: pp-10506 ⋅ Poprawnie: 216/282 [76%]
Rozwiąż
Podpunkt 31.1 (1 pkt)
Punkt
O jest środkiem a prosta jest styczną
to tego okręgu, przy czym
\alpha=70^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 32. 1 pkt ⋅ Numer: pp-10507 ⋅ Poprawnie: 73/100 [73%]
Rozwiąż
Podpunkt 32.1 (1 pkt)
Suma miar kąta środkowego okręgu i kąta wpisanego w ten okrąg, opartego są na tym samym łuku
jest równa
120 .
Oblicz miarę kąta środkowego.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 33. 1 pkt ⋅ Numer: pp-10508 ⋅ Poprawnie: 78/131 [59%]
Rozwiąż
Podpunkt 33.1 (1 pkt)
» Kąt
\alpha wpisany w okrąg o promieniu długości
18
oparty jest na łuku o długości
6\pi .
Wyznacz miarę tego kąta.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 34. 1 pkt ⋅ Numer: pp-10509 ⋅ Poprawnie: 39/61 [63%]
Rozwiąż
Podpunkt 34.1 (1 pkt)
«« Kąt wpisany w okrąg o promieniu długości
15 ma miarę
72^{\circ} . Kąt ten oparty jest na łuku o długości
k\cdot \pi .
Wyznacz liczbę k .
Odpowiedź:
k=
(wpisz liczbę całkowitą)
Zadanie 35. 1 pkt ⋅ Numer: pp-10510 ⋅ Poprawnie: 81/143 [56%]
Rozwiąż
Podpunkt 35.1 (1 pkt)
Na łuku okręgu o długości równej
\frac{1}{5} długości okręgu, oparto dwa kąty:
kąt wpisany w ten okrąg i kąt środkowy tego okręgu.
Wyznacz sumę miar stopniowych tych kątów.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
Zadanie 36. 1 pkt ⋅ Numer: pp-10511 ⋅ Poprawnie: 147/201 [73%]
Rozwiąż
Podpunkt 36.1 (1 pkt)
Kąt
\alpha na rysunku ma miarę
50^{\circ} :
Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 37. 1 pkt ⋅ Numer: pp-10512 ⋅ Poprawnie: 187/251 [74%]
Rozwiąż
Podpunkt 37.1 (1 pkt)
Punkt
O na rysunku jest środkiem okręgu, a kąty mają miary
\alpha=105^{\circ} oraz
\beta=95^{\circ} :
Wyznacz miarę stopniową kąta ABC .
Odpowiedź:
|\sphericalangle ABC|=
(wpisz liczbę całkowitą)
Zadanie 38. 1 pkt ⋅ Numer: pp-10513 ⋅ Poprawnie: 152/257 [59%]
Rozwiąż
Podpunkt 38.1 (1 pkt)
Punkt
O jest środkiem okręgu na rysunku, a kąt:
\alpha ma miarę
210^{\circ} :
Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 39. 1 pkt ⋅ Numer: pp-10538 ⋅ Poprawnie: 139/246 [56%]
Rozwiąż
Podpunkt 39.1 (1 pkt)
Punkt
O jest środkiem okręgu:
Wyznacz miarę stopniową kąta ACO .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 40. 1 pkt ⋅ Numer: pp-10516 ⋅ Poprawnie: 164/225 [72%]
Rozwiąż
Podpunkt 40.1 (1 pkt)
Punkt
O jest środkiem okręgu, a kąty mają miary
\alpha=30^{\circ} oraz
\beta=35^{\circ} :
Wyznacz miarę stopniową kąta
\gamma .
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 41. 1 pkt ⋅ Numer: pp-10517 ⋅ Poprawnie: 196/272 [72%]
Rozwiąż
Podpunkt 41.1 (1 pkt)
Punkt
O jest środkiem okręgu, przy czym
\alpha=120^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 42. 1 pkt ⋅ Numer: pp-10518 ⋅ Poprawnie: 187/269 [69%]
Rozwiąż
Podpunkt 42.1 (1 pkt)
Punkt
O jest środkiem okręgu,
kąt
\alpha ma miarę
260^{\circ}
a prosta jest styczna do tego okręgu:
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 43. 1 pkt ⋅ Numer: pp-10519 ⋅ Poprawnie: 27/56 [48%]
Rozwiąż
Podpunkt 43.1 (1 pkt)
Na okręgu o środku
O zaznaczono
k=15
wierzchołków wielokąta foremnego. Spośród nich wybrano trzy kolejne i narysowano kąt
jak na rysunku:
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 44. 1 pkt ⋅ Numer: pp-10520 ⋅ Poprawnie: 54/108 [50%]
Rozwiąż
Podpunkt 44.1 (1 pkt)
Na okręgu zaznaczono wierzchołki
30 -kąta foremnego.
Spośród nich wybrano pięć kolejnych i narysowano kąt jak na rysunku:
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 45. 1 pkt ⋅ Numer: pp-10521 ⋅ Poprawnie: 49/145 [33%]
Rozwiąż
Podpunkt 45.1 (1 pkt)
«« Na okręgu zaznaczono wierzchołki
36 -kąta foremnego.
Spośród nich wybrano siedem kolejnych i narysowano kąt jak na rysunku:
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 46. 1 pkt ⋅ Numer: pp-10522 ⋅ Poprawnie: 236/330 [71%]
Rozwiąż
Podpunkt 46.1 (1 pkt)
Punkt
O jest środkiem okręgu, a prosta jest styczną
do tego okręgu, przy czym
\beta=55^{\circ} :
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 47. 1 pkt ⋅ Numer: pp-10523 ⋅ Poprawnie: 67/108 [62%]
Rozwiąż
Podpunkt 47.1 (1 pkt)
Punkt
O jest środkiem okręgu, a kąt
\alpha
ma miarę
60^{\circ} :
Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 48. 1 pkt ⋅ Numer: pp-10524 ⋅ Poprawnie: 148/203 [72%]
Rozwiąż
Podpunkt 48.1 (1 pkt)
Prosta jest styczną do okręgu, a kąty
\alpha i
\beta mają miary:
\alpha=40^{\circ} oraz
\beta=52^{\circ} :
Wyznacz miarę stopniową kąta \gamma .
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 49. 1 pkt ⋅ Numer: pp-10525 ⋅ Poprawnie: 78/125 [62%]
Rozwiąż
Podpunkt 49.1 (1 pkt)
Punkt
O jest środkiem okręgu, przy czym
\alpha=154^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 50. 1 pkt ⋅ Numer: pp-11414 ⋅ Poprawnie: 56/94 [59%]
Rozwiąż
Podpunkt 50.1 (1 pkt)
» Trójkąt
ABC jest równoramienny o podstawie
AB , odcinek
CD
jest średnicą okręgu oraz
\alpha=40^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 51. 1 pkt ⋅ Numer: pp-11445 ⋅ Poprawnie: 51/189 [26%]
Rozwiąż
Podpunkt 51.1 (1 pkt)
« Trójkąt
ABC jest równoramienny o podstawie
AB , odcinek
CD
jest średnicą okręgu oraz
\alpha=40^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 52. 1 pkt ⋅ Numer: pp-10529 ⋅ Poprawnie: 63/98 [64%]
Rozwiąż
Podpunkt 52.1 (1 pkt)
Punkt
O jest środkiem okręgu oraz
\alpha=35^{\circ} i
\beta=23^{\circ} :
Wyznacz miarę stopniopwą kąta \gamma .
Odpowiedź:
\gamma=
(wpisz liczbę całkowitą)
Zadanie 53. 1 pkt ⋅ Numer: pp-10530 ⋅ Poprawnie: 110/144 [76%]
Rozwiąż
Podpunkt 53.1 (1 pkt)
Dany jest okrąg o środku w punkcie
S , w którym
a=72^{\circ} :
Oblicz sumę miar stopniowych kątów
\beta i \gamma .
Odpowiedź:
\beta+\gamma=
(wpisz liczbę całkowitą)
Zadanie 54. 1 pkt ⋅ Numer: pp-10531 ⋅ Poprawnie: 99/134 [73%]
Rozwiąż
Podpunkt 54.1 (1 pkt)
Punkt
O jest środkiem okręgu, przy czym
\alpha=27^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
Zadanie 55. 1 pkt ⋅ Numer: pp-10532 ⋅ Poprawnie: 30/66 [45%]
Rozwiąż
Podpunkt 55.1 (1 pkt)
Punkt
O jest środkiem okręgu, przy czym
\beta=60^{\circ}
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
Zadanie 56. 1 pkt ⋅ Numer: pp-10533 ⋅ Poprawnie: 119/147 [80%]
Rozwiąż
Podpunkt 56.1 (1 pkt)
Punkt
O jest środkiem okręgu:
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 57. 1 pkt ⋅ Numer: pp-10534 ⋅ Poprawnie: 109/128 [85%]
Rozwiąż
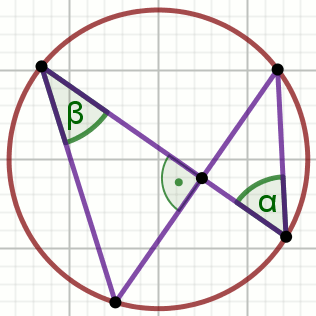
Podpunkt 57.1 (1 pkt)
Punkty
A ,
B i
C leżą na okręgu o środku
O :
Wyznacz miarę stopniową zaznaczonego na rysunku wypukłego kąta środkowego
AOB .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 58. 1 pkt ⋅ Numer: pp-10545 ⋅ Poprawnie: 81/112 [72%]
Rozwiąż
Podpunkt 58.1 (1 pkt)
Punkt
O jest środkiem okręgu, a prosta
k styczną do tego okręgu w punkcie
A :
.
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
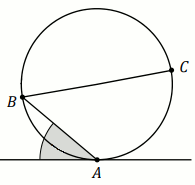
Zadanie 59. 1 pkt ⋅ Numer: pp-10501 ⋅ Poprawnie: 31/96 [32%]
Rozwiąż
Podpunkt 59.1 (1 pkt)
» Stosunek obwodu zacieniowanej części koła do obwodu całego koła wynosi:
Odpowiedzi:
A. \frac{3}{4}
B. \frac{4+\pi}{4\pi}
C. \frac{1}{4}
D. \frac{4+\pi}{2\pi}
Zadanie 60. 1 pkt ⋅ Numer: pp-10487 ⋅ Poprawnie: 50/62 [80%]
Rozwiąż
Podpunkt 60.1 (1 pkt)
W czworokącie
OBMA kąty wewnętrzne
AOB i
AMB mają równe
miary.
Wyznacz miarę stopniową kąta \alpha .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 61. 1 pkt ⋅ Numer: pp-10540 ⋅ Poprawnie: 52/65 [80%]
Rozwiąż
Podpunkt 61.1 (1 pkt)
« O godzinie 1020
Odpowiedzi:
A. 170^{\circ}
B. 162^{\circ}
C. 160^{\circ}
D. 165^{\circ}
Zadanie 62. 1 pkt ⋅ Numer: pp-10497 ⋅ Poprawnie: 52/88 [59%]
Rozwiąż
Podpunkt 62.1 (1 pkt)
W okręgu poprowadzono cięciwę
AB oraz cięciwę
BC (
A\neq C ). Obie
cięciwy mają długość równą promieniowi okręgu.
Wyznacz miarę stopniową kąta ABC .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 63. 1 pkt ⋅ Numer: pp-11513 ⋅ Poprawnie: 456/830 [54%]
Rozwiąż
Podpunkt 63.1 (1 pkt)
(1 pkt)
Punkt
O jest środkiem okręgu na rysunku, a kąt
\alpha ma miarę
33^{\circ} :
Wyznacz miarę stopniową kąta \beta .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
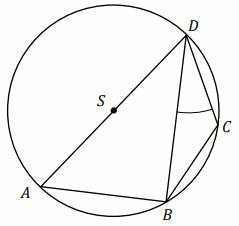
Zadanie 64. 1 pkt ⋅ Numer: pp-11543 ⋅ Poprawnie: 102/178 [57%]
Rozwiąż
Podpunkt 64.1 (1 pkt)
(1 pkt)
Trójkąty
ABC i
ADC są wpisane w okrąg o środku
S , przy czym
S\in CD . Kąt
\alpha
ma miarę
45^{\circ} , odcinek
AC długość
14 :
Średnica tego okręgu ma długość:
Odpowiedzi:
A. 14
B. \frac{28\sqrt{2}}{3}
C. 14\sqrt{2}
D. 21\sqrt{2}
E. 21
F. 7\sqrt{2}
Zadanie 65. 1 pkt ⋅ Numer: pp-11756 ⋅ Poprawnie: 15/39 [38%]
Rozwiąż
Podpunkt 65.1 (1 pkt)
(1 pkt)
Trójkąty
ABC i
ADC są wpisane w okrąg o środku
S , przy czym
S\in CD . Kąt
\alpha
ma miarę
45^{\circ} , odcinek
AC długość
14\sqrt{2} :
Średnica tego okręgu ma długość:
Odpowiedzi:
A. 28\sqrt{2}
B. 14
C. 28
D. \frac{28\sqrt{2}}{3}
E. 14\sqrt{2}
F. 21
Zadanie 66. 1 pkt ⋅ Numer: pp-11544 ⋅ Poprawnie: 44/134 [32%]
Rozwiąż
Podpunkt 66.1 (1 pkt)
(1 pkt)
Odcinek
AB jest średnicą okręgu o środku w punkcie
S
i promieniu
r o długości
22 . Na przedłużeniu półprostej
AB^{\rightarrow} zaznaczono punkt
D taki, że odcinek
BD ma długość równą promieniowi okręgu, a następnie
przez punkt
D poprowadzono styczną do tego okręgu w punkcie
C :
Wówczas cięciwa
AC ma długość:
Odpowiedzi:
A. 44
B. 33
C. 22\sqrt{2}
D. 22\sqrt{3}
E. 44\sqrt{3}
F. 11\sqrt{3}
Zadanie 67. 1 pkt ⋅ Numer: pp-11755 ⋅ Poprawnie: 27/39 [69%]
Rozwiąż
Podpunkt 67.1 (1 pkt)
(1 pkt)
Odcinek
AB jest średnicą okręgu o środku w punkcie
S
i promieniu
r o długości
22 . Na przedłużeniu półprostej
AB^{\rightarrow} zaznaczono punkt
D taki, że odcinek
BD ma długość równą promieniowi okręgu, a następnie
przez punkt
D poprowadzono styczną do tego okręgu w punkcie
C :
Wówczas odległość punktu
S od cięciwy
AC jest równa:
Odpowiedzi:
A. \frac{22}{3}
B. \frac{22\sqrt{3}}{3}
C. 11
D. \frac{11\sqrt{2}}{2}
E. 22\sqrt{2}
F. \frac{11\sqrt{3}}{2}
Zadanie 68. 1 pkt ⋅ Numer: pp-11770 ⋅ Poprawnie: 695/845 [82%]
Rozwiąż
Podpunkt 68.1 (1 pkt)
Punkty
A ,
B i
C
należą do okręgu o środku w punkcie
O , a kąt
\alpha ma miarę
62^{\circ} :
Miara kąta \beta jest równa:
Odpowiedzi:
A. 24^{\circ}
B. 32^{\circ}
C. 30^{\circ}
D. 28^{\circ}
Zadanie 69. 1 pkt ⋅ Numer: pp-11793 ⋅ Poprawnie: 654/842 [77%]
Rozwiąż
Podpunkt 69.1 (1 pkt)
Na łukach
AB i
CD okręgu są oparte kąty wpisane
ADB i
DBC , takie, że
\alpha=22^{\circ} i
\beta=36^{\circ} (zobacz rysunek).
Cięciwy
AC i
BD przecinają się w punkcie
K .
Miara kąta DKC jest równa:
Odpowiedzi:
A. 54^{\circ}
B. 66^{\circ}
C. 52^{\circ}
D. 62^{\circ}
E. 58^{\circ}
F. 60^{\circ}
Zadanie 70. 1 pkt ⋅ Numer: pp-11819 ⋅ Poprawnie: 511/696 [73%]
Rozwiąż
Podpunkt 70.1 (1 pkt)
Koło ma promień równy
4 .
Obwód wycinka tego koła o kącie środkowym 45^{\circ} jest równy:
Odpowiedzi:
A. 4+\frac{1}{2}\pi
B. 16+1
C. 16+2\pi
D. 8+\frac{1}{2}\pi
E. 8+\pi
F. 8+2\pi
Zadanie 71. 1 pkt ⋅ Numer: pp-11820 ⋅ Poprawnie: 526/668 [78%]
Rozwiąż
Podpunkt 71.1 (1 pkt)
W okręgu
\mathcal{O} kąt środkowy
\beta
oraz kąt wpisany
\alpha są oparte na tym samym łuku.
Kąt
\beta ma miarę o
50^{\circ} większą od kąta
\alpha .
Miara kąta \beta jest równa:
Odpowiedzi:
A. 75^{\circ}
B. 100^{\circ}
C. 50^{\circ}
D. \frac{350}{3}^{\circ}
E. \frac{250}{3}^{\circ}
F. 150^{\circ}
Zadanie 72. 1 pkt ⋅ Numer: pp-11845 ⋅ Poprawnie: 493/641 [76%]
Rozwiąż
Podpunkt 72.1 (1 pkt)
Punkty
A ,
B oraz
C
leżą na okręgu o środku w punkcie
O . Prosta
k
jest styczna do tego okręgu w punkcie
A i tworzy z cięciwą
AB kąt o mierze
44^{\circ} . Ponadto odcinek
AC jest średnicą tego okręgu (zobacz rysunek).
Miara kąta rozwartego BOC jest równa:
Odpowiedzi:
A. 86^{\circ}
B. 90^{\circ}
C. 88^{\circ}
D. 84^{\circ}
E. 94^{\circ}
F. 92^{\circ}
Zadanie 73. 1 pkt ⋅ Numer: pp-11866 ⋅ Poprawnie: 137/228 [60%]
Rozwiąż
Podpunkt 73.1 (1 pkt)
Punkty
A ,
B ,
C
leżą na okręgu o środku
S . Punkt
D jest punktem
przecięcia cięciwy
AC i średnicy okręgu poprowadzonej z punktu
B . Miara kąta
BSC jest równa
134^{\circ} , a miara kąta
ADB jest równa
\gamma (zobacz rysunek).
Wtedy kąt ABD ma miarę:
Odpowiedzi:
A. 73^{\circ}-\gamma
B. 113^{\circ}-2\gamma
C. 147^{\circ}-\gamma
D. 91^{\circ}-\gamma
E. 113^{\circ}-\gamma
F. 136^{\circ}-\frac{\gamma}{2}
Zadanie 74. 1 pkt ⋅ Numer: pp-11874 ⋅ Poprawnie: 171/256 [66%]
Rozwiąż
Podpunkt 74.1 (1 pkt)
Punkty
A ,
B ,
P leżą
na okręgu o środku
S i promieniu długości
8 .
Czworokąt
ASBP jest rombem, w którym kąt ostry
PAS
ma miarę
60^{\circ} (zobacz rysunek).
Pole powierzchni zakreskowanej na rysunku figury jest równe:
Odpowiedzi:
A. 64\pi
B. 16\pi
C. \frac{64}{3}\pi
D. \frac{16}{3}\pi
E. \frac{32}{3}\pi
F. \frac{128}{3}\pi
Zadanie 75. 1 pkt ⋅ Numer: pp-11892 ⋅ Poprawnie: 116/149 [77%]
Rozwiąż
Podpunkt 75.1 (1 pkt)
Na trójkącie ostrokątnym
ABC opisano okrąg o środku
O .
Miara kąta
ABC jest równa
64^{\circ} .
Miara kąta ACO jest równa:
Odpowiedzi:
A. 21^{\circ}
B. 26^{\circ}
C. 30^{\circ}
D. 22^{\circ}
E. 34^{\circ}
F. 24^{\circ}
Zadanie 76. 1 pkt ⋅ Numer: pp-11923 ⋅ Poprawnie: 127/187 [67%]
Rozwiąż
Podpunkt 76.1 (1 pkt)
Wierzchołki
A ,
B ,
C
czworokąta
ABSC leżą na okręgu o środku
S .
Kąt
ABS ma miarę
50^{\circ} (zobacz rysunek),
a przekątna
BC jest dwusieczną tego kąta.
Miara kąta ASC jest równa:
Odpowiedzi:
A. 42^{\circ}
B. 70^{\circ}
C. 50^{\circ}
D. 56^{\circ}
E. 62^{\circ}
F. 54^{\circ}
Zadanie 77. 1 pkt ⋅ Numer: pp-11924 ⋅ Poprawnie: 139/187 [74%]
Rozwiąż
Podpunkt 77.1 (1 pkt)
Punkty
A oraz
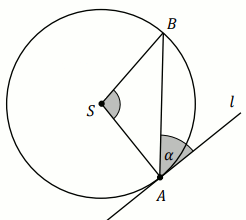
B leżą na okręgu o środku
S . Kąt środkowy
ASB ma miarę
120^{\circ} . Prosta
l jest styczna do
tego okręgu w punkcie
A i tworzy z cięciwą
AB
okręgu kąt o mierze
\alpha (zobacz rysunek).
Wtedy:
Odpowiedzi:
A. \alpha=70^{\circ}
B. \alpha=52^{\circ}
C. \alpha=60^{\circ}
D. \alpha=64^{\circ}
E. \alpha=66^{\circ}
F. \alpha=48^{\circ}
Zadanie 78. 1 pkt ⋅ Numer: pp-11953 ⋅ Poprawnie: 46/79 [58%]
Rozwiąż
Podpunkt 78.1 (1 pkt)
Punkty
A ,
B oraz
C
należą do okręgu o środku w punkcie
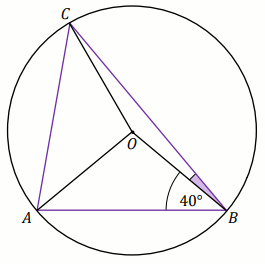
O . Kąt
ABO ma miarę
40^{\circ} , a kąt
OBC ma miarę
16^{\circ} (zobacz rysunek).
Miara kąta ACO jest równa:
Odpowiedzi:
A. 37^{\circ}
B. 33^{\circ}
C. 34^{\circ}
D. 30^{\circ}
E. 35^{\circ}
F. 36^{\circ}
Zadanie 79. 1 pkt ⋅ Numer: pp-11971 ⋅ Poprawnie: 39/58 [67%]
Rozwiąż
Podpunkt 79.1 (1 pkt)
Punkty
A ,
B ,
C
leżą na okręgu o środku
O (zobacz rysunek).
Ponadto
|\sphericalangle BOA}|=110^{\circ} .
Miara kąta CAB jest równa:
Odpowiedzi:
A. 63^{\circ}
B. 62^{\circ}
C. 60^{\circ}
D. 64^{\circ}
E. 56^{\circ}
F. 66^{\circ}
Zadanie 80. 1 pkt ⋅ Numer: pp-11996 ⋅ Poprawnie: 415/660 [62%]
Rozwiąż
Podpunkt 80.1 (1 pkt)
W trójkącie
ABC , wpisanym w okrąg o środku w punkcie
S ,
kąt
ACB ma miarę
47^{\circ} (zobacz rysunek).
Miara kąta ostrego BAS jest równa:
Odpowiedzi:
A. 46^{\circ}
B. 43^{\circ}
C. 48^{\circ}
D. 41^{\circ}
E. 47^{\circ}
F. 39^{\circ}
Zadanie 81. 1 pkt ⋅ Numer: pp-12017 ⋅ Poprawnie: 220/361 [60%]
Rozwiąż
Podpunkt 81.1 (1 pkt)
Punkty
A ,
B oraz
C
leżą na okręgu o środku w punkcie
S . Długość łuku
AB ,
na którym jest oparty kąt wpisany
ACB , jest równa
\frac{1}{6} długości okręgu (zobacz rysunek).
Miara stopniowa kąta ostrego ACB jest równa:
Odpowiedzi:
A. 28^{\circ}
B. 30^{\circ}
C. 32^{\circ}
D. 33^{\circ}
E. 46^{\circ}
F. 42^{\circ}
Zadanie 82. 1 pkt ⋅ Numer: pp-12036 ⋅ Poprawnie: 50/57 [87%]
Rozwiąż
Podpunkt 82.1 (1 pkt)
Trójkąt
ABC jest wpisany w okrąg o środku
O .
Miara kąta
CAO jest równa
60^{\circ}
(zobacz rysunek).
Wtedy miara stopniowa kąta ABC jest równa:
Odpowiedzi:
A. 25^{\circ}
B. 32^{\circ}
C. 30^{\circ}
D. 26^{\circ}
E. 33^{\circ}
F. 28^{\circ}
Zadanie 83. 1 pkt ⋅ Numer: pp-12072 ⋅ Poprawnie: 26/45 [57%]
Rozwiąż
Podpunkt 83.1 (1 pkt)
Punkty
A ,
B ,
C
i
D leżą na okręgu o środku
S . Miary kątów
SBC ,
BCD ,
CDA
są równe odpowiednio:
60^{\circ} ,
115^{\circ} ,
90^{\circ} (zobacz rysunek).
Wynika z tego, że miara \alpha jest równa:
Odpowiedzi:
A. 35^{\circ}
B. 38^{\circ}
C. 31^{\circ}
D. 40^{\circ}
E. 32^{\circ}
F. 33^{\circ}
G. 29^{\circ}
H. 39^{\circ}
Zadanie 84. 1 pkt ⋅ Numer: pp-12093 ⋅ Poprawnie: 15/21 [71%]
Rozwiąż
Podpunkt 84.1 (1 pkt)
Na okręgu o środku w punkcie
O leżą punkty
A ,
B oraz
C . Odcinek
AC jest średnicą tego okręgu, a kąt środkowy
AOB ma miarę
66^{\circ} (zobacz rysunek).
Miara kąta OBC jest równa:
Odpowiedzi:
A. 31^{\circ}
B. 36^{\circ}
C. 27^{\circ}
D. 30^{\circ}
E. 38^{\circ}
F. 35^{\circ}
G. 28^{\circ}
H. 33^{\circ}
Zadanie 85. 1 pkt ⋅ Numer: pp-12094 ⋅ Poprawnie: 12/18 [66%]
Rozwiąż
Podpunkt 85.1 (1 pkt)
Dane są okrąg i prosta styczna do tego okręgu w punkcie
A .
Punkty
B i
C są położone na okręgu tak,
że
BC jest jego średnicą. Cięciwa
AB
tworzy ze styczną kąt o mierze
39^{\circ} (zobacz rysunek).
Miara kąta ABC jest równa:
Odpowiedzi:
A. 49^{\circ}
B. 53^{\circ}
C. 56^{\circ}
D. 55^{\circ}
E. 51^{\circ}
F. 57^{\circ}
G. 54^{\circ}
H. 46^{\circ}
Zadanie 86. 1 pkt ⋅ Numer: pp-12123 ⋅ Poprawnie: 20/22 [90%]
Rozwiąż
Podpunkt 86.1 (1 pkt)
Czworokąt
ABCD jest wpisany w okrąg o środku
S . Bok
AD jest średnicą tego okręgu,
a miara kąta
BDC jest równa
27^{\circ} (zobacz rysunek).
Wtedy miara stopniowa kąta BSC jest równa:
Odpowiedzi:
A. 48^{\circ}
B. 52^{\circ}
C. 53^{\circ}
D. 58^{\circ}
E. 51^{\circ}
F. 59^{\circ}
G. 56^{\circ}
H. 54^{\circ}
Zadanie 87. 1 pkt ⋅ Numer: pp-12125 ⋅ Poprawnie: 15/22 [68%]
Rozwiąż
Podpunkt 87.1 (1 pkt)
Punkty
A ,
B ,
C i
D leżą na okręgu o środku w punkcie
O .
Cięciwy
DB i
AC przecinają się
w punkcie
E ,
|\sphericalangle ACB|=50^{\circ} oraz
|\sphericalangle AEB|=135^{\circ} (zobacz rysunek).
Miara stopniowa kąta DAC jest równa:
Odpowiedzi:
A. 83^{\circ}
B. 90^{\circ}
C. 82^{\circ}
D. 85^{\circ}
E. 81^{\circ}
F. 84^{\circ}
G. 87^{\circ}
H. 91^{\circ}
Zadanie 88. 1 pkt ⋅ Numer: pp-12149 ⋅ Poprawnie: 74/129 [57%]
Rozwiąż
Podpunkt 88.1 (1 pkt)
Punkty
K ,
L oraz
M
należą do okręgu o środku w punkcie
S . Miara kąta
KSM jest równa
134^{\circ}
(zobacz rysunek).
Miara kąta wpisanego w ten okrąg KLM jest równa:
Odpowiedzi:
A. 120^{\circ}
B. 108^{\circ}
C. 107^{\circ}
D. 113^{\circ}
E. 115^{\circ}
F. 105^{\circ}
G. 111^{\circ}
H. 118^{\circ}
Zadanie 89. 1 pkt ⋅ Numer: pp-12376 ⋅ Poprawnie: 149/185 [80%]
Rozwiąż
Podpunkt 89.1 (1 pkt)
Dany jest okrąg o środku w punkcie
S i promieniu
36 .
Miara kąta wpisanego
ACB jest równa
45^{\circ} (zobacz rysunek).
Długość łuku AB , na którym oparty jest kąt wpisany ACB ,
jest równa:
Odpowiedzi:
A. 12\pi
B. 27\pi
C. \frac{72}{5}\pi
D. 24\pi
E. 45\pi
F. 18\pi
Zadanie 90. 1 pkt ⋅ Numer: pp-11531 ⋅ Poprawnie: 375/426 [88%]
Rozwiąż
Podpunkt 90.1 (1 pkt)
Punkty
A ,
B oraz
C
leżą na okręgu o środku w punkcie
O . Miara kąta
BCA jest równa
50^{\circ} (zobacz rysunek).
Miara kąta ostrego ABO jest równa:
Odpowiedzi:
A. 40^{\circ}
B. 44^{\circ}
C. 37^{\circ}
D. 43^{\circ}
E. 36^{\circ}
F. 45^{\circ}
G. 39^{\circ}
H. 42^{\circ}
Zadanie 91. 1 pkt ⋅ Numer: pp-12413 ⋅ Poprawnie: 248/304 [81%]
Rozwiąż
Podpunkt 91.1 (1 pkt)
Na dziesięciokącie foremnym
ABCDEFGHIJ opisano okrąg o środku w
punkcie
S (zobacz rysunek).
Miara kąta środkowego okręgu ASD jest równa:
Odpowiedzi:
A. 105^{\circ}
B. 104^{\circ}
C. 116^{\circ}
D. 107^{\circ}
E. 113^{\circ}
F. 111^{\circ}
G. 112^{\circ}
H. 108^{\circ}
Zadanie 92. 2 pkt ⋅ Numer: pp-20201 ⋅ Poprawnie: 64/161 [39%]
Rozwiąż
Podpunkt 92.1 (1 pkt)
» Na trójkącie
ABC opisano okrąg.
W punkcie
C poprowadzono styczną do okręgu, jak
na rysunku.
Wiedząc, że
CE jest dwusieczną kąta
BCA oblicz miary kątów trójkąta
EFC .
Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=44^{\circ} \beta=80^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 92.2 (1 pkt)
Podaj miarę stopniową największego z kątów tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 93. 2 pkt ⋅ Numer: pp-20202 ⋅ Poprawnie: 73/149 [48%]
Rozwiąż
Podpunkt 93.1 (1 pkt)
« Na trójkącie
ABC opisano okrąg.
Z punktu
P leżącego poza okręgiem poprowadzono
styczną do okręgu w punkcie
A oraz sieczną,
która przecięła okrąg w punktach
B i
C .
Oblicz miary kątów trójkąta
APC .
Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=55^{\circ} \beta=85^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 93.2 (1 pkt)
Podaj miarę stopniową największego z kątów tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 94. 2 pkt ⋅ Numer: pp-20203 ⋅ Poprawnie: 50/101 [49%]
Rozwiąż
Podpunkt 94.1 (2 pkt)
Brązowy czworokąt na rysunku jest prostokątem:
Oblicz miarę stopniową kąta \alpha .
Dane
\beta=60^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 95. 2 pkt ⋅ Numer: pp-20204 ⋅ Poprawnie: 30/79 [37%]
Rozwiąż
Podpunkt 95.1 (2 pkt)
» Korzystając z danych na rysunku oblicz miarę stopniową
kąta
\beta:
Dane
\alpha=45^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 96. 2 pkt ⋅ Numer: pp-20783 ⋅ Poprawnie: 54/91 [59%]
Rozwiąż
Podpunkt 96.1 (2 pkt)
Z punktu
C leżącego poza okręgiem poprowadzono
sieczną okręgu zawierającą środek okręgu
S oraz
taką sieczną przecinającą ten okrąg w punktach
A
i
B , że
|SB|=|BC| .
Oblicz |\sphericalangle ASD| .
Dane
|\sphericalangle BCE|=18^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 97. 2 pkt ⋅ Numer: pp-20784 ⋅ Poprawnie: 25/76 [32%]
Rozwiąż
Podpunkt 97.1 (2 pkt)
Z punktu
C leżącego poza okręgiem poprowadzono
sieczną okręgu zawierającą środek okręgu
S oraz
taką sieczną przecinającą ten okrąg w punktach
A
i
B , że
|SB|=|BC| .
Oblicz |\sphericalangle BCS| .
Dane
|\sphericalangle ASD|=48^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 98. 2 pkt ⋅ Numer: pp-20207 ⋅ Poprawnie: 45/136 [33%]
Rozwiąż
Podpunkt 98.1 (1 pkt)
« Punkt
O jest środkiem okręgu, w którym
AB\parallel CD :
Podaj miarę stopniową kąta \beta .
Dane
\alpha=32^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 98.2 (1 pkt)
Podaj miarę stopniową kąta
\gamma .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 99. 2 pkt ⋅ Numer: pp-20208 ⋅ Poprawnie: 87/169 [51%]
Rozwiąż
Podpunkt 99.1 (2 pkt)
Punkt
O jest środkiem okręgu. Oblicz miarę
stopniową kąta
\alpha zaznaczonego na rysunku.
Dane
\beta=47^{\circ} \gamma=138^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 100. 2 pkt ⋅ Numer: pp-20205 ⋅ Poprawnie: 11/22 [50%]
Rozwiąż
Podpunkt 100.1 (1 pkt)
» W okrąg wpisano trójkąt
ABC ,
w którym
|\sphericalangle A|=42^{\circ} oraz
|\sphericalangle B|=61^{\circ} . Poprowadzono styczną
do okręgu w punkcie
C , która przecięła przedłużenie
boku
AB w punkcie
D .
Oblicz miary kątów trójkąta
BDC .
Podaj miarę stopniową najmniejszego kąta tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 100.2 (1 pkt)
Podaj miarę stopniową największego kąta tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 101. 2 pkt ⋅ Numer: pp-20206 ⋅ Poprawnie: 73/156 [46%]
Rozwiąż
Podpunkt 101.1 (2 pkt)
Kąt między cięciwą
AB a styczną do okręgu w punkcie
B ma miarę
30^{\circ} .
Korzystając z danych na rysunku oblicz miarę kąta
ABC .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 102. 2 pkt ⋅ Numer: pp-20809 ⋅ Poprawnie: 30/325 [9%]
Rozwiąż
Podpunkt 102.1 (1 pkt)
(1 pkt) Punkt
O jest środkiem, a odcinek
AC średnicą okręgu na rysunku.
W okrąg ten wpisano kąt
ABC , a następnie odcinek
BC przedłużono do takiego punktu
D , że
|BC|=|CD| .
Wiedząc, że kąt BOD jest prosty, oblicz pole
powierzchni trójkąta ABO .
Dane
a=14
Odpowiedź:
Podpunkt 102.2 (1 pkt)
(1 pkt) Łuk, na którym oparty jest mniejszy z kątów
środkowych okręgu
AOE , ma długość
p\cdot\pi .
Wyznacz liczbę p .
Odpowiedź:
(wpisz dwie liczby całkowite)
Zadanie 103. 2 pkt ⋅ Numer: pp-21064 ⋅ Poprawnie: 274/654 [41%]
Rozwiąż
Podpunkt 103.1 (2 pkt)
Dany jest okrąg
\mathcal{O} o środku w punkcie
S .
Średnica
AB tego okręgu przecina cięciwę
CD
w punkcie
P (zobacz rysunek). Ponadto:
|PB|=2 ,
|PC|=4 oraz
|PD|=5 .
Oblicz promień okręgu \mathcal{O} .
Odpowiedź:
(wpisz dwie liczby całkowite)
☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat
Masz pytania? Napisz: k42195@poczta.fm


 .
.