Okrąg opisany na trójkącie
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- symetralne boków trójkąta
- okrąg opisany na trójkącie
- promień okręgu opisanego
- punkt przecięcia symetralnych
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10551 |
Podpunkt 1.1 (1 pkt)
» Wielokąt na rysunku jest foremny, w którym |AB|=\frac{\sqrt{6}}{2}:
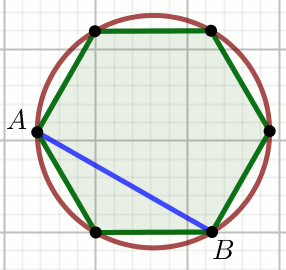
Pole powierzchni koła opisanego na tym wielokącie jest równe p\cdot\pi.
Wyznacz liczbę p.
Odpowiedź:
| p= | |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10552 |
Podpunkt 2.1 (1 pkt)
Pięciokąt na rysunku jest foremny:
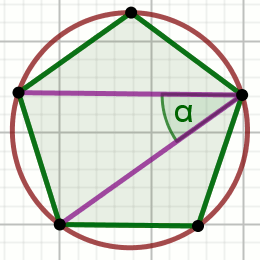
Wyznacz miarę stopniową zaznaczonego na rysunku kąta \alpha.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20210 |
Podpunkt 3.1 (1 pkt)
« Na trójkącie rozwartokątnym ABC, w którym kąt
przy wierzchołku C jest rozwarty, opisano okrąg
o środku w punkcie S. Kąt środkowy
BSC ma miarę \alpha,
zaś kąt środkowy wypukły ASB miarę
\beta. Oblicz miary kątów trójkąta
ABC.
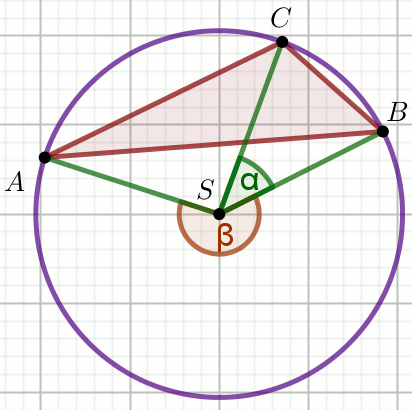
Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=32^{\circ}
\beta=202^{\circ}
\beta=202^{\circ}
Odpowiedź:
\gamma_{min}=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
Podaj miarę stopniową największego z kątów.
Odpowiedź:
\gamma_{max}=
(wpisz liczbę całkowitą)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20211 |
Podpunkt 4.1 (1 pkt)
« Na trójkącie ostrokątnym ABC opisano okrąg
o środku w punkcie O. Wiedząc, że
|\measuredangle CBO|=\alpha oraz
|\measuredangle CAO|=\beta oblicz miary
stopniowe kątów trójkąta ABC.
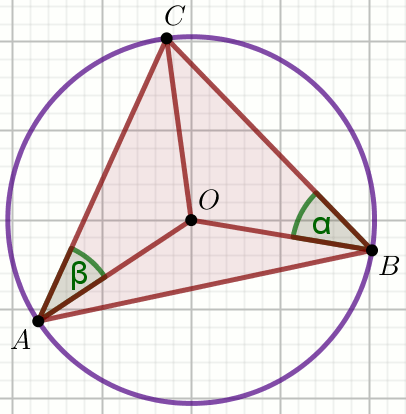
Podaj miarę stopniową najmniejszego z kątów tego trójkąta.
Dane
\alpha=10^{\circ}
\beta=48^{\circ}
\beta=48^{\circ}
Odpowiedź:
\gamma_{min}=
(wpisz liczbę całkowitą)
Podpunkt 4.2 (1 pkt)
Podaj miarę stopniową największego z kątów tego trójkąta.
Odpowiedź:
\gamma_{max}=
(wpisz liczbę całkowitą)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20212 |
Podpunkt 5.1 (1 pkt)
« Na trójkącie ABCopisano okrąg. Wierzchołki trójkąta
podzieliły okrąg na trzy łuki AB,
BC i CA, które pozostają w
stosunku x:y:z.
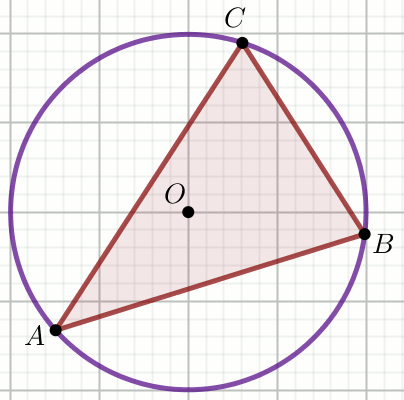
Podaj miarę stopniową najmniejszego kąta tego trójkąta.
Dane
x=4
y=18
z=8
y=18
z=8
Odpowiedź:
| \gamma_{min}= | |
Podpunkt 5.2 (1 pkt)
Podaj miarę stopniową największego kąta tego trójkąta.
Odpowiedź:
| \gamma_{max}= | |
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20215 |
Podpunkt 6.1 (2 pkt)
» Punkt O jest środkiem okręgu, do którego
należą punkty A, B i
C, jak na rysunku:
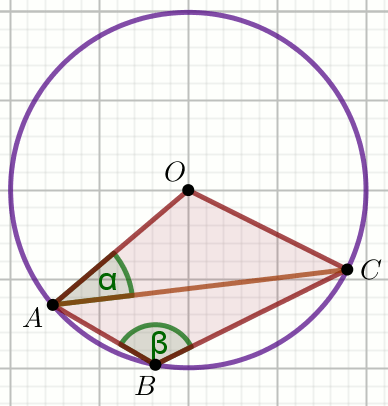
Wiedząc, że |\measuredangle OAC|=\alpha, oblicz
\beta.
Dane
\alpha=14^{\circ}
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20232 |
Podpunkt 7.1 (2 pkt)
Korzystając z danych oraz rysunku oblicz y:
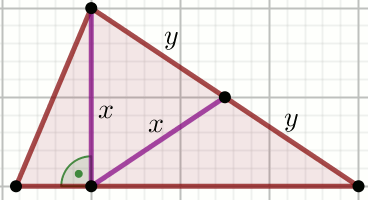
Dane
x=2\sqrt{2}=2.82842712474619
Odpowiedź:
y=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21019 |
Podpunkt 8.1 (2 pkt)
« W trójkącie ABC bok BC jest dłuższy od boku AC, a wysokość
CD ma długość 9. Symetralna boku AB
przecina ten bok w punkcie E, a bok
BC w punkcie F.
Wiedząc, że |EF|=6 oblicz stosunek |BD|:|AD|.
Odpowiedź:
| |BD|:|AD|= | |