Okrąg opisany na trójkącie
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- symetralne boków trójkąta
- okrąg opisany na trójkącie
- promień okręgu opisanego
- punkt przecięcia symetralnych
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10557 |
Podpunkt 1.1 (1 pkt)
Okrąg jest opisany na prostokącie o bokach długości 5
i 5\sqrt{2}.
Oblicz długość promienia tego okręgu.
Odpowiedź:
| r= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10556 |
Podpunkt 2.1 (1 pkt)
« Trójkąt ma przyprostokątne długości 5 i
5\sqrt{2}. Pole powierzchni koła opisanego na tym trójkącie jest
równe p\cdot \pi.
Oblicz liczbę p.
Odpowiedź:
| p= | |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10554 |
Podpunkt 3.1 (1 pkt)
Na kwadracie opisano koło o promieniu długości 7\sqrt{6}.
Oblicz długość promienia koła wpisanego w ten kwadrat.
Odpowiedź:
r=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10549 |
Podpunkt 4.1 (1 pkt)
« Oblicz pole powierzchni kwadratu wpisanego w okrąg o promieniu
długości \frac{\sqrt{2}}{5}.
Odpowiedź:
| P_{\square}= | |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10573 |
Podpunkt 5.1 (1 pkt)
» W trójkącie prostokątnym ABC kąt przy
wierzchołku A jest prosty, punkt
E jest środkiem boku AB,
zaś punkt D spodkiem wysokości opuszczonej z
wierzchołka kąta prostego A. Ponadto
|DE|=12.
Oblicz długość odcinka AB.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10555 |
Podpunkt 6.1 (1 pkt)
W okrąg o promieniu 8\sqrt{2} wpisano kwadrat, a następnie
w ten kwadrat wpisano okrąg o promieniu r.
Oblicz r.
Odpowiedź:
r=
(liczba zapisana dziesiętnie)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11685 |
Podpunkt 7.1 (1 pkt)
Promień okręgu opisanego na trójkącie prostokatnym ma długość 3\sqrt{11}.
Kąt przy wierzchołku A tego trójkąta jest prosty, a jego środkowe przecinają się
w punkcie S.
Oblicz długość odcinka AS.
Odpowiedź:
| |AS|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20716 |
Podpunkt 8.1 (2 pkt)
Niebieski odcinek jest wysokością trójkąta na rysunku. Korzystając z danych oraz rysunku oblicz
długość promienia tego okręgu:
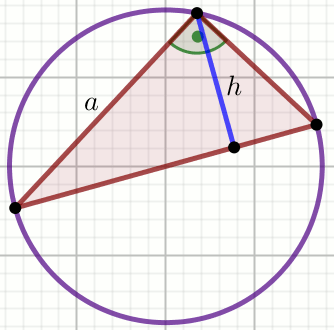
Dane
a=30
h=\frac{240}{17}=14.11764705882350
h=\frac{240}{17}=14.11764705882350
Odpowiedź:
| R= | |
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20957 |
Podpunkt 9.1 (2 pkt)
Na trójkącie prostokątnym opisano okrąg o środku w punkcie O.
Środkowe tego trojkąta przecinają się w punkcie S.
Przeciwprostokątna tego trójkąta jest o \frac{125}{12} dłuższa od długości
odcinka OS.
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | |
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20216 |
Podpunkt 10.1 (2 pkt)
Okrąg opisano na trójkącie o bokach długości
a, b i
c. Oblicz długość promienia tego okręgu.
Dane
a=\sqrt{3}=1.73205080756888
b=\sqrt{11}=3.31662479035540
c=\sqrt{14}=3.74165738677394
b=\sqrt{11}=3.31662479035540
c=\sqrt{14}=3.74165738677394
Odpowiedź:
| R= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 11. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21014 |
Podpunkt 11.1 (1 pkt)
W trójkącie prostokątnym boki przyległe do kąta prostego mają długość
7 i 24. Na trójkącie tym
opisano okrąg.
Oblicz długość promienia tego okręgu.
Odpowiedź:
| R= | |
Podpunkt 11.2 (1 pkt)
Oblicz odległość środka ciężkości tego trójkąta od środka okręgu opisanego na tym trójkącie.
Odpowiedź:
| d= | |
Podpunkt 11.3 (1 pkt)
Oblicz odległość spodka wysokości opuszczonej na przeciwprostokątną tego trójkąta od środka okręgu
opisanego na tym trójkącie.
Odpowiedź:
| d= | |
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30300 |
Podpunkt 12.1 (2 pkt)
« Spodek wysokości opuszczonej z wierzchołka kąta prostego trójkata prostokatnego
leży w odległości d od środka okręgu opisanego na tym
trójkącie, a wysokość ta ma długość h.
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Dane
d=7=7.00000000000000
h=24
h=24
Odpowiedź:
| R= | |
Podpunkt 12.2 (2 pkt)
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
L=
(liczba zapisana dziesiętnie)