Okrąg opisany na trójkącie
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- symetralne boków trójkąta
- okrąg opisany na trójkącie
- promień okręgu opisanego
- punkt przecięcia symetralnych
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20209 |
Podpunkt 1.1 (2 pkt)
« Na trójkącie równoramiennym ABC, w którym
|AC|=|BC| i kąt między ramionami trójkąta ma
miarę \alpha, opisano okrąg o środku w punkcie
S.
Półprosta BS^{\to} przecina bok
AC trójkąta w punkcie K.
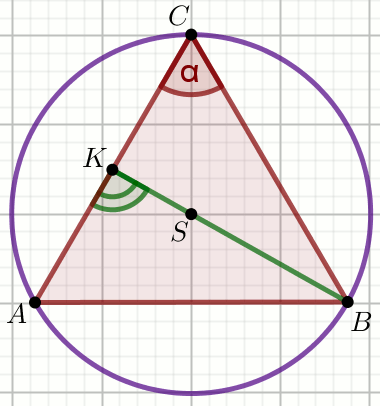

Wyznacz miarę stopniową kąta AKB.
Dane
\alpha=32^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20213 |
Podpunkt 2.1 (2 pkt)
Punkt O jest środkiem okręgu opisanego
na trójkącie równoramiennym ABC o podstawie
AB. Kąt OBC ma miarę
\alpha.
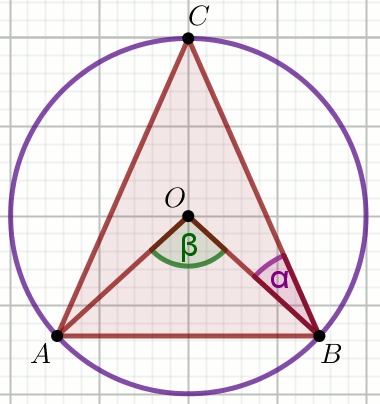

Oblicz \beta.
Dane
\alpha=16^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20715 |
Podpunkt 3.1 (2 pkt)
Podstawa trójkąta równoramiennego ma długość a, a jego
ramię długość c.
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Dane
a=48
c=40
c=40
Odpowiedź:
| r= | |
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20958 |
Podpunkt 4.1 (2 pkt)
W trójkącie ABC boki AC i BC
mają równą długość równą \sqrt{197}, a promień okręgu opisanego na tym
trójkącie ma długość \frac{197}{2}.
Oblicz długość boku AB tego trójkąta.
Odpowiedź:
|AB|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20959 |
Podpunkt 5.1 (2 pkt)
Symetralne boków trójkąta równoramiennego ABC o podstawie
AB, przecinają się w punkcie S.
Punkt S jest odległy do wierzchołka A
o \frac{18}{5}, a od boku BC
o \frac{3\sqrt{11}}{5}.
Oblicz długość boku AB tego trójkąta.
Odpowiedź:
|AB|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21008 |
Podpunkt 6.1 (1 pkt)
W trójkącie równoramiennym ABC o podstawie AB
kąt przy wierzchołku C ma miarę 120^{\circ}.
Symetralne tego trójkąta przecinają się w punkcie P.
Wiedząc, że |CP|=\sqrt{3}, oblicz długość podstawy tego trójkąta
Odpowiedź:
| |AB|= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 6.2 (1 pkt)
Oblicz długość ramienia tego trójkąta
Odpowiedź:
|AC|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)