Okrąg wpisany w trójkąt
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- okrąg wpisany
- dwusieczne kątów trójkąta
- środek okręgu wpisanego w trójkąt
- promień okręgu wpisanego w trójkąt
- twierdzenie o dwusiecznej trójkąta
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20023 |
Podpunkt 1.1 (2 pkt)
« AM i CN są
dwusiecznymi kątów \alpha i
\gamma w trójkącie ABC.
Dwusieczne te przecinają się w punkcie S. Wiedząc,
że na czworokącie NBMS można opisać okrąg oblicz
\frac{\alpha+\gamma}{2}.
Podaj obliczoną miarę stopniową.
Odpowiedź:
\frac{\alpha+\gamma}{2}=
(wpisz liczbę całkowitą)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20739 |
Podpunkt 2.1 (2 pkt)
«« Dany jest trójkąt:
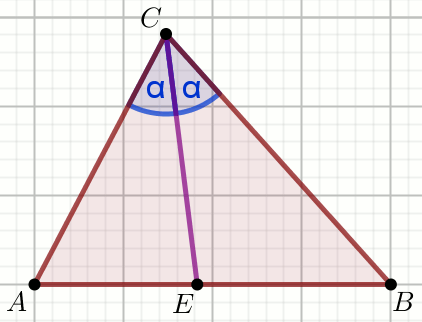

Oblicz |AE|.
Dane
|AB|=\frac{12}{5}=2.40000000000000
|AC|=\frac{6}{5}=1.20000000000000
|BC|=2=2.00000000000000
|AC|=\frac{6}{5}=1.20000000000000
|BC|=2=2.00000000000000
Odpowiedź:
| |AE|= | |
| Zadanie 3. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30005 |
Podpunkt 3.1 (4 pkt)
» W trójkąt ABC wpisano okrąg o promieniu
4, który jest styczny do boków
AB, BC i
CA odpowiednio w punktach
P, Q i
R.
Wiedząc, że |BQ|=8, |CQ|=4, oblicz pole tego trójkąta.
Odpowiedź:
P_{\triangle}=
(wpisz liczbę całkowitą)
| Zadanie 4. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30852 |
Podpunkt 4.1 (2 pkt)
Bok AC trójkąta ABC ma długość
17, a wysokość CD długość
15. Dwusieczna kąta BAC przecina bok
BC w punkcie P, który jest odległy od boku
AB o \frac{1800}{137}.
Oblicz długość boku AB.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 4.2 (2 pkt)
Oblicz długość boku BC.
Odpowiedź:
|BC|=
(wpisz liczbę całkowitą)
| Zadanie 5. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30853 |
Podpunkt 5.1 (2 pkt)
W trójkąt rozwartokątny ABC, w którym |AC|=|BC|,
wpisano okrąg o środku w punkcie O i promiemiu równym
30. Punkt P jest punktem styczności tego okręgu
z ramieniem AC, a symetralna boku AC przecina ten bok
w punkcie M oraz symetralną boku AB w punkcie
S. Wiedząc, że |PM|=52.0 oraz
|MS|=127.5, oblicz promień R okręgu opisanego
na trójkącie ABC oraz długość boku AB.
Podaj R.
Odpowiedź:
| R= | |
Podpunkt 5.2 (2 pkt)
Podaj |AB|.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
| Zadanie 6. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30854 |
Podpunkt 6.1 (4 pkt)
W trójkącie ABC bok AC ma długość
17. Wysokość CD dzieli bok
AB na odcinki AD i DB.
Dwusieczna kąta BAC przecina bok BC w punkcie
P. Wiedząc, że |AD|=8 i
|DB|=112 oblicz odległość d punktu P
od podstawy AB tego trójkąta.
Podaj obliczoną odległość.
Odpowiedź:
| d= | |