Okrąg wpisany w trójkąt
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- okrąg wpisany
- dwusieczne kątów trójkąta
- środek okręgu wpisanego w trójkąt
- promień okręgu wpisanego w trójkąt
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10560 |
Podpunkt 1.1 (1 pkt)
« W trójkąt równoramienny ABC o podstawie
AB wpisano okrąg o środku O.
Wiadomo, że |\sphericalangle BOA|=138^{\circ}.
Oblicz miarę stopniową kąta BCA.
Odpowiedź:
|\sphericalangle BCA|=
(wpisz liczbę całkowitą)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10574 |
Podpunkt 2.1 (1 pkt)
W trójkącie ABC, w którym
|AC|=|BC| i
|\sphericalangle BCA|=60^{\circ}, poprowadzono
dwusieczną AD.
Wyznacz miarę stopniową kąta ADC.
Odpowiedź:
|\sphericalangle ADC|=
(wpisz liczbę całkowitą)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10576 |
Podpunkt 3.1 (1 pkt)
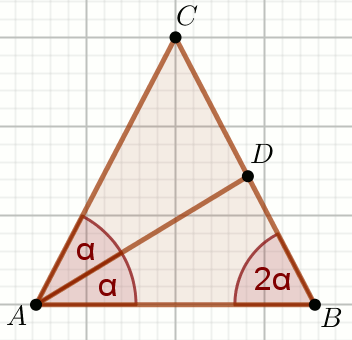
» Trójkąt ABC na rysunku jest równoramienny,
a AD jest dwusieczną kąta przy wierzchołku
A, przy czym |\sphericalangle B|=52^{\circ}:

Wyznacz miarę stopniową kąta \alpha.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20720 |
Podpunkt 4.1 (2 pkt)
« Dany jest trójkąt:
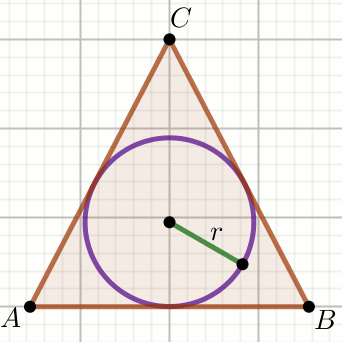

Oblicz r.
Dane
|AB|=32
|AC|=20
|BC|=20
|AC|=20
|BC|=20
Odpowiedź:
| r= | |
| Zadanie 5. (3 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20960 |
Podpunkt 5.1 (1 pkt)
Dany jest trójkąt ostrokątny ABC, w którym
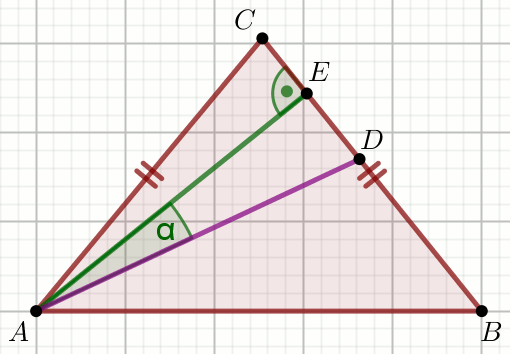
|CD|=\frac{578}{33} i |BD|=\frac{544}{33}:

Oblicz |AB|.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 5.2 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | |
Podpunkt 5.3 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
| r= | |
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20962 |
Podpunkt 6.1 (1 pkt)
W trójkącie równoramiennym ABC, w którym |AC|=|BC|,
dwusieczna kąta o wierzchołku A przeciecięła bok BC
w punkcie D takim, że |BD|=\frac{18}{5} i
|CD|=\frac{27}{5}.
Oblicz długość podstawy AB tego trójkąta.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Odcinek DE jest wysokością trójkąta ABD.
Oblicz długość odcinka EB.
Odpowiedź:
| |EB|= | |
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21013 |
Podpunkt 7.1 (1 pkt)
« W trójkącie równoramiennym ABC o podstawie AB
dane są długości boków: |AC|=|BC|=52 i |AB|=40.
W trójkąt ten wpisano okrąg.
Oblicz długości odcinków, na które dwusieczna kąta przy podstawie podzieliła ramię tego trójkąta.
Odpowiedzi:
| min | = |
(wpisz liczbę zapisaną dziesiętnie) |
| max | = |
(wpisz liczbę zapisaną dziesiętnie) |
Podpunkt 7.2 (1 pkt)
Oblicz długości odcinków, na które punkt styczności okręgu z ramieniem trójkąta podzielił to ramię.
Odpowiedzi:
| min | = |
(wpisz liczbę zapisaną dziesiętnie) |
| max | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-21022 |
Podpunkt 8.1 (1 pkt)
W trójkącie równoramiennym ABC, w którym |AC|=|BC|,
wysokość CD ma długośc 21, a promień okręgu
wpisanego w ten trójkąt ma długość \frac{60}{7}.
Oblicz długość boku AB.
Odpowiedź:
|AB|=
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Oblicz długość boku AC.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20217 |
Podpunkt 9.1 (2 pkt)
«« Trójkąt równoramienny ABC o podstawie
AB jest ostrokątny. W trójkąt ten wpisano okrąg
o środku S, przy czym kąt
|\sphericalangle SAB|=\alpha.
Oblicz |\sphericalangle BCA|.
Dane
\alpha=38^{\circ}
Odpowiedź:
|\sphericalangle BCA|=
(wpisz liczbę całkowitą)
| Zadanie 10. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-30401 |
Podpunkt 10.1 (1 pkt)
W trójkącie równoramiennym ABC podstawa AB
ma długość 42, a wysokość AD długość
33.6. Dwusieczna kąta ABC przecina bok
AC w punkcie P.
Oblicz długość ramion tego trójkąta.
Odpowiedź:
|AC|=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
Oblicz długość odcinków AP i CP.
Odpowiedzi:
| |AP| | = |
(wpisz liczbę zapisaną dziesiętnie) |
| |CP| | = |
(wpisz liczbę zapisaną dziesiętnie) |
Podpunkt 10.3 (2 pkt)
Oblicz długość odcinka BP.
Odpowiedź:
| |BP|= | ||
| (wpisz trzy liczby całkowite) | ||