⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Wykresy funkcji trygonometrycznych
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- wykresy funkcji trygonometrycznych
- przekształcenia wykresów
- symetrie wykresów
- przesunięcie o wektor wykresu funkcji
| Zadanie 1. 1 pkt ⋅ Numer: pr-10147 ⋅ Poprawnie: 169/213 [79%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Dana jest funkcja g(x)=3\cos^4x-3\sin^4x-5,
której zbiorem wartości jest przedział \langle a,b\rangle.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pr-10149 ⋅ Poprawnie: 186/272 [68%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Wyznacz okres podstawowy funkcji określonej wzorem
g(x)=\cos\left(\frac{3}{2}\pi+2\pi x\right).
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 3. 1 pkt ⋅ Numer: pr-11641 ⋅ Poprawnie: 7/15 [46%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji f określonej dla każdej
liczby rzeczywistej x:
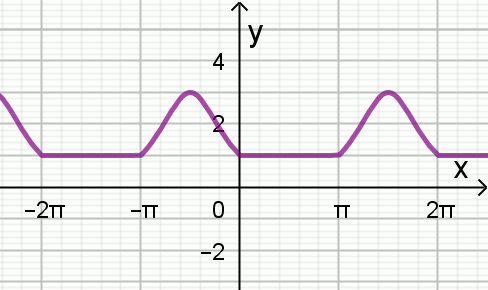
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji f.
Odpowiedzi:
| A. f(x)=\frac{\sin{x}-2}{|\sin{x}|-2} | B. f(x)=\frac{|\cos{x}|-2}{\cos{x}-2} |
| C. f(x)=\frac{|\sin{x}|-2}{\cos{x}-2} | D. f(x)=\frac{|\sin{x}|+1}{\sin{x}-1} |
| E. f(x)=\frac{|\cos{x}|-2}{\sin{x}-2} | F. f(x)=\frac{\cos{x}-2}{|\sin{x}|-2} |
| Zadanie 4. 1 pkt ⋅ Numer: pr-11647 ⋅ Poprawnie: 13/31 [41%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu pewnej funkcji f określonej dla
każdej liczby rzeczywistej x. Jeden z podanych poniżej wzorów jest wzorem
tej funkcji.
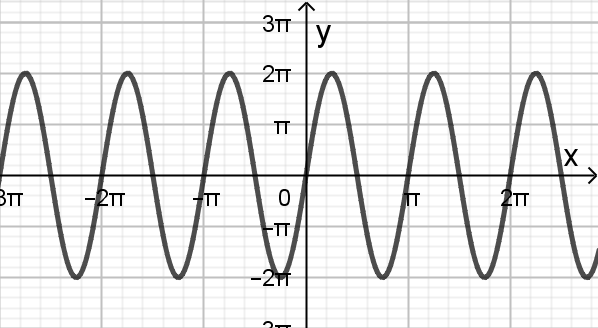
Wskaż wzór funkcji f.
Odpowiedzi:
| A. f(x)=2\cdot\sin{2x} | B. f(x)=2\pi\cdot\sin{\frac{1}{2}x} |
| C. f(x)=2\cdot\sin{\frac{1}{2}x} | D. f(x)=2\pi\cdot\sin{x} |
| E. f(x)=2\cdot\sin{x} | F. f(x)=2\pi\cdot\sin{2x} |
| Zadanie 5. 4 pkt ⋅ Numer: pr-30197 ⋅ Poprawnie: 18/64 [28%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
» Wyznacz te wartości parametru m, dla których
równanie
4\sin^2 2x\cdot \cos^2 2x+\frac{m+2}{2m-16}=4
nie jest sprzeczne.
Podaj najmniejsze możliwe m spełniające warunki zadania.
Odpowiedź:
| m_{min}= | |
Podpunkt 5.2 (2 pkt)
Podaj największe możliwe m spełniające warunki
zadania.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)
| Zadanie 6. 4 pkt ⋅ Numer: pr-30202 ⋅ Poprawnie: 58/144 [40%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Funkcja f określona jest wzorem
f(x)=-2\cos^2 x-6\cos x-\frac{3}{2},
gdzie x\in\langle 0,2\pi\rangle.
Wyznacz ZW_f.
Podaj najmniejszą wartość tej funkcji.
Odpowiedź:
| min= | |
Podpunkt 6.2 (2 pkt)
Podaj największą wartość tej funkcji.
Odpowiedź:
| max= | |
| Zadanie 7. 4 pkt ⋅ Numer: pr-30201 ⋅ Poprawnie: 7/25 [28%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Funkcja g określona jest wzorem
g(x)=\cos\left(\frac{1}{2}\pi+x\right)+\sin(-x)-2,
gdzie x\in\langle \pi,2\pi\rangle.
Dla jakich wartości parametru m równanie
g(x)=\frac{m-3}{2}-3 ma rozwiązania należące
do przedziału \langle \pi,2\pi\rangle?
Podaj najmniejsze możliwe m spełniające warunki zadania.
Odpowiedź:
m_{min}=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (2 pkt)
Podaj największe możliwe m spełniające warunki
zadania.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)
| Zadanie 8. 4 pkt ⋅ Numer: pr-30204 ⋅ Poprawnie: 40/67 [59%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Dana jest funkcja
f(x)=\sqrt{1-\cos^2\left(x+\frac{\pi}{2}\right)}
, gdzie x\in(-\pi,\pi).
Narysuj wykres funkcji f. Na podstawie wykresu
ustal dla jakich wartości parametru m
równanie f(x)=\frac{m-2}{2} ma co najmniej jedno rozwiązanie
należące do przedziału
\left\langle -\frac{\pi}{3},\frac{\pi}{3}\right\rangle?
Podaj najmniejsze możliwe m spełniające warunki zadania.
Odpowiedź:
| m_{min}= | |
Podpunkt 8.2 (2 pkt)
Podaj największe możliwe m spełniające warunki
zadania.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)
| Zadanie 9. 4 pkt ⋅ Numer: pr-30875 ⋅ Poprawnie: 4/27 [14%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« Dana jest funkcja
f(x)=\sqrt{1-\sin^2\left(x+\frac{\pi}{2}\right)}
, gdzie x\in(-\pi,\pi).
Narysuj wykres funkcji f. Na podstawie wykresu
ustal dla jakich wartości parametru m
równanie f(x)=\frac{m-5}{2} ma co najmniej jedno rozwiązanie
należące do przedziału
\left\langle -\frac{\pi}{3},\frac{\pi}{3}\right\rangle?
Podaj najmniejsze możliwe m spełniające warunki zadania.
Odpowiedź:
| m_{min}= | |
Podpunkt 9.2 (2 pkt)
Podaj największe możliwe m spełniające warunki
zadania.
Odpowiedź:
m_{max}=
(wpisz liczbę całkowitą)