⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Twierdzenie sinusów
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- twierdzenie sinusów
- wzór sinusów
- funkcje trygonometryczne w dowolnym trójkącie
- promień okręgu opisanego na trójkącie
- rozwiązywanie trójkątów
- związki miarowe w trójkącie
| Zadanie 1. 2 pkt ⋅ Numer: pr-20565 ⋅ Poprawnie: 83/65 [127%] | Rozwiąż |
Podpunkt 1.1 (2 pkt)
« Dany jest trójkąt:
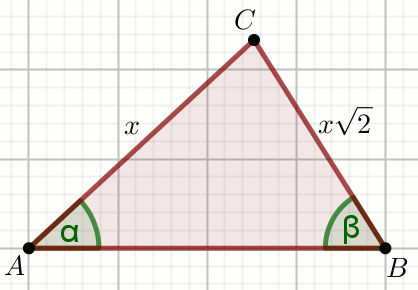
Wiedząc, że x=6, oblicz \frac{\cos^2\alpha}{2\cos^2\beta-1}.
Odpowiedź:
| \frac{\cos^2\alpha}{2\cos^2\beta-1}= | |
| Zadanie 2. 2 pkt ⋅ Numer: pr-20738 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
» W trójkącie ostrokątnym ABC dane są:
długość boku |AB|=42 oraz tangens kąta przy
wierzchołku C: \tan\gamma=\frac{40}{9}.
Oblicz długość promienia koła opisanego na tym trójkącie.
Odpowiedź:
| R= | |
| Zadanie 3. 2 pkt ⋅ Numer: pr-20770 ⋅ Poprawnie: 77/65 [118%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Dwa boki trójkąta mają długość 9 i
7. Dowolny punkt boku trzeciego połączono
z wierzchołkiem kąta naprzeciwległego odcinkiem, który podzielił
ten trójkąta na dwa mniejsze trójkąty.
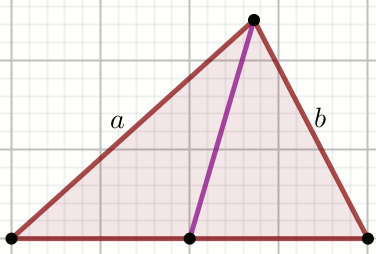
Oblicz stosunek długości promieni okręgów opisanych na otrzymanych trójkątach. Podaj wartość tego stosunku należącą do przedziału \langle 1,+\infty).
Odpowiedź:
| r_1:r_2= | |
| Zadanie 4. 2 pkt ⋅ Numer: pr-20769 ⋅ Poprawnie: 82/65 [126%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Dany jest trójkąt ABC, w którym
|BC|=\frac{7\sqrt{2}}{3},
|\sphericalangle CAB|=45^{\circ},
|\sphericalangle BCA|=30^{\circ}.
Oblicz |AB|.
Odpowiedź:
| |AB|= | |
| Zadanie 5. 3 pkt ⋅ Numer: pr-21195 ⋅ Poprawnie: 18/29 [62%] | Rozwiąż |
Podpunkt 5.1 (3 pkt)
W trójkącie ABC kąt BAC jest dwa razy większy od
kąta ABC o mierze \alpha. Niech |BC|=a,
|AC|=b oraz |AB|=c. Wówczas
\cos\alpha=\frac{b+c}{k\cdot a}, gdzie k jest
pewną liczbą rzeczywistą.
Podaj liczbę k.
Odpowiedź:
| k= | |