Twierdzenie cosinusów
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- twierdzenie cosinusów
- wzory cosinusów
- funkcje trygonometryczne w dowolnym trójkącie
- cosinus kąta w trójkącie
- rozwiązywanie trójkątów
- związki miarowe w trójkącie
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20883 |
Podpunkt 1.1 (1 pkt)
« Kąt ostry DAB równoległoboku
ABCD, w którym |AB|=5 i
|AD|=10, ma miarę 60^{\circ}.
Oblicz długość krótszej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 1.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20884 |
Podpunkt 2.1 (1 pkt)
Dwa boki trójkąta mają długość 14 i
7, a \alpha jest kątem
zawartym między nimi, przy czym \sin\alpha=\frac{\sqrt{195}}{14}.
Wyznacz najmniejszą możliwą długość trzeciego boku tego trójkąta.
Odpowiedź:
c_{min}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 2.2 (1 pkt)
Wyznacz największą możliwą długość trzeciego boku tego trójkąta.
Odpowiedź:
c_{max}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20885 |
Podpunkt 3.1 (2 pkt)
« Dany jest trójkąt ABC, w którym
|AB|=2\sqrt{3},
|BC|=2 i
|AC|=2.
Oblicz miarę kąta CAB.
Odpowiedź:
|\sphericalangle CAB|=
(wpisz liczbę całkowitą)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20886 |
Podpunkt 4.1 (2 pkt)
» Oblicz długość niebieskiego odcinka na rysunku wiedząc, że:
|AD|=90,
|DB|=3,
|AC|=106,
|BC|=\sqrt{3145}:
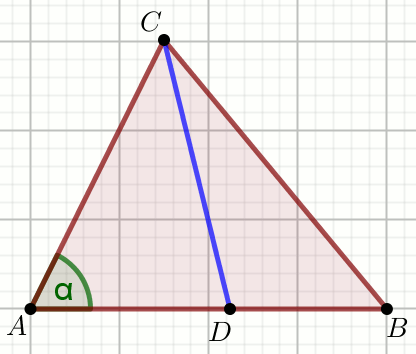
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20887 |
Podpunkt 5.1 (2 pkt)
» Oblicz długość promienia okręgu na rysunku wiedząc, że
|AC|-|AB|=48\sqrt{2} oraz
|BC|=80:
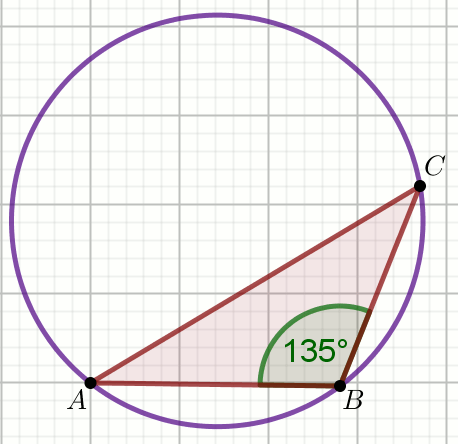
Odpowiedź:
R=
(wpisz liczbę całkowitą)
Liczba wyświetlonych zadań: 5
Liczba pozostałych zadań dostępnych dla zarejestrowanych nauczycieli: 4