Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Twierdzenie cosinusów

Zadania dla liceum ogólnokształcącego - poziom rozszerzony

 

Zadanie 1.  2 pkt ⋅ Numer: pr-20745 ⋅ Poprawnie: 76/161 [47%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 « Dany jest trójkąt ABC, w którym d=4 i |AC|=8:

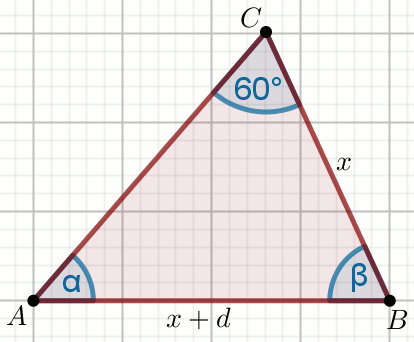
Oblicz \sin\alpha.

Odpowiedź:
\sin\alpha= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 1.2 (1 pkt)
 Oblicz \sin\beta.
Odpowiedź:
\sin\beta= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 2.  2 pkt ⋅ Numer: pr-20747 ⋅ Poprawnie: 38/89 [42%] Rozwiąż 
Podpunkt 2.1 (2 pkt)
 « Trójkąt na rysunku jest równoboczny, a liczba k jest równa 8:

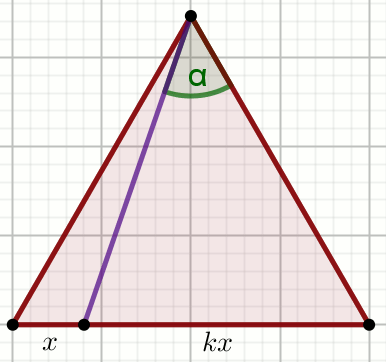
Oblicz \sin\alpha.

Odpowiedź:
\sin\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 3.  2 pkt ⋅ Numer: pr-20746 ⋅ Poprawnie: 25/51 [49%] Rozwiąż 
Podpunkt 3.1 (2 pkt)
» Dany jest trójkąt:

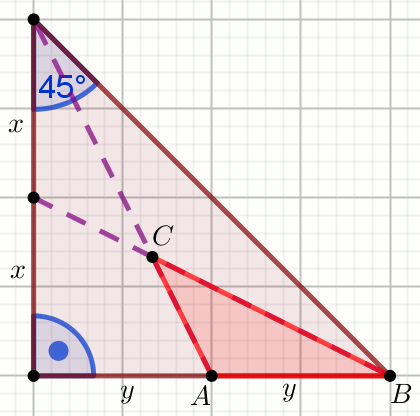
Oblicz \cos\sphericalangle BCA.

Odpowiedź:
\cos\sphericalangle BCA=
(wpisz dwie liczby całkowite)
Zadanie 4.  2 pkt ⋅ Numer: pr-21196 ⋅ Poprawnie: 1/2 [50%] Rozwiąż 
Podpunkt 4.1 (2 pkt)
 W trójkącie ABC bok AB jest 2 razy dłuższy od boku AC, a długość boku BC stanowi \frac{9}{7} długości boku AC.

Oblicz cosinus najmniejszego kąta trójkąta ABC.

Odpowiedź:
\cos\alpha=
(wpisz dwie liczby całkowite)
Zadanie 5.  4 pkt ⋅ Numer: pr-30348 ⋅ Poprawnie: 43/98 [43%] Rozwiąż 
Podpunkt 5.1 (4 pkt)
 » Odcinki na rysunku maja długość: a=96, b=84 i c=36:

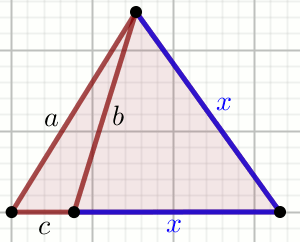
Oblicz obwód trójkąta na rysunku.

Odpowiedź:
L= (wpisz liczbę całkowitą)
Zadanie 6.  4 pkt ⋅ Numer: pr-30379 ⋅ Poprawnie: 27/80 [33%] Rozwiąż 
Podpunkt 6.1 (2 pkt)
 «« Pole powierzchni trójkąta o kącie ostrym 30^{\circ} jest równe 36\sqrt{3}, a promień okręgu na nim opisanego ma długość 12.

Podaj długość najdłuższego boku tego trójkąta.

Odpowiedź:
a_{max}= \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 6.2 (1 pkt)
 Podaj długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R= (wpisz liczbę całkowitą)
Podpunkt 6.3 (1 pkt)
 Podaj długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 7.  4 pkt ⋅ Numer: pr-30380 ⋅ Poprawnie: 26/80 [32%] Rozwiąż 
Podpunkt 7.1 (4 pkt)
 « W trójkącie na rysunku dane są długości odcinków: |AD|=1, |DB|=\frac{5}{2}, |BC|=2\sqrt{2} i |AC|=\frac{5}{2}:

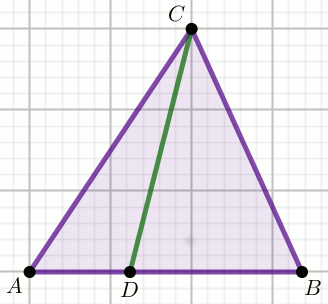
Oblicz \sin\sphericalangle{ADC}.

Odpowiedź:
\sin\sphericalangle{ADC}= (liczba zapisana dziesiętnie)
Zadanie 8.  4 pkt ⋅ Numer: pr-30794 ⋅ Poprawnie: 21/78 [26%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 W prostokącie ABCD dane są długości boków |AB|=52 i |AD|=48. Na boku CD zaznaczono punkt E taki, że |DE|=32, zaś na odcinku EB punkt M taki, że |EM|=48 (zobacz rysunek).

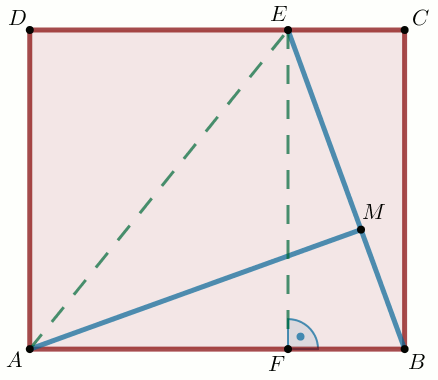
Wykorzystując podane poniżej długości odcinków oblicz pole powierzchni trójkąta ABM.

Odpowiedź:
P_{ABM}= (wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
 Oblicz długość odcinka AM.
Odpowiedź:
|AM|= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 8.3 (2 pkt)
 Oblicz długość promienia okręgu opisanego na trójkącie ABM.
Odpowiedź:
R= \cdot√
(wpisz trzy liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm