Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Pole trójkąta cz.1

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-10678 ⋅ Poprawnie: 417/517 [80%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 » Oblicz pole powierzchni rombu o boku długości 40 i kącie rozwartym 120^{\circ}.
Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 2.  1 pkt ⋅ Numer: pp-10647 ⋅ Poprawnie: 380/531 [71%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 W trójkącie równoramiennym ramię o długości 7\sqrt{3} tworzy z podstawą kąt o mierze 67,5^{\circ}.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 3.  1 pkt ⋅ Numer: pp-10669 ⋅ Poprawnie: 402/594 [67%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 Dany jest trójkąt ABC, w którym |AB|=4, |BC|=12 oraz \sin\sphericalangle ABC=\frac{2\sqrt{2}}{3}.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle ABC}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 4.  1 pkt ⋅ Numer: pp-10655 ⋅ Poprawnie: 365/619 [58%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 « Bok rombu ma długość 9, a jego kąt ostry miarę \alpha taką, że \cos\alpha=\frac{\sqrt{3}}{3}.

Oblicz pole powierzchni tego rombu.

Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 5.  1 pkt ⋅ Numer: pp-10654 ⋅ Poprawnie: 235/355 [66%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 Oblicz pole powierzchni równoległoboku o bokach długości \frac{7}{3} i 4 oraz kącie ostrym o mierze 30^{\circ}.
Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 6.  1 pkt ⋅ Numer: pp-10666 ⋅ Poprawnie: 258/455 [56%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 « Przyprostokątna trójkąta o długości 9 jest jednym z ramion kąta ostrego tego trójkąta o mierze 30^{\circ}

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 7.  1 pkt ⋅ Numer: pp-10673 ⋅ Poprawnie: 230/347 [66%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 » Przekątne równoległoboku o długości 7 i \frac{3}{4} przecinają się pod kątem rozwartym o mierze 150^{\circ}.

Oblicz pole powierzchni tego równoległoboku.

Odpowiedź:
P=
(wpisz dwie liczby całkowite)
Zadanie 8.  1 pkt ⋅ Numer: pp-10656 ⋅ Poprawnie: 354/511 [69%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 « Przekątne równoległoboku mają długość 2 i 6, a kąt między tymi przekątnymi ma miarę 30^{\circ}.

Oblicz pole powierzchni tego równoległoboku.

Odpowiedź:
P=
(wpisz dwie liczby całkowite)
Zadanie 9.  1 pkt ⋅ Numer: pp-11512 ⋅ Poprawnie: 483/859 [56%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Oblicz pole powierzchni prostokąta,którego przekątne mają długość 16 i przecinają się pod kątem o mierze 30^{\circ}.
Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 10.  1 pkt ⋅ Numer: pp-10667 ⋅ Poprawnie: 258/335 [77%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 Każde z ramion trójkąta równoramiennego ma długość 30. Kąt zawarty między ramionami tego trójkąta ma miarę 120^{\circ}.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 11.  1 pkt ⋅ Numer: pp-10679 ⋅ Poprawnie: 172/233 [73%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 Pole powierzchni rombu o obwodzie długości 56 jest równe 49. Kąt ostry tego rombu ma miarę \alpha.

Wówczas:

Odpowiedzi:
A. 60^{\circ} \lessdot \alpha \lessdot 61^{\circ} B. 29^{\circ} \lessdot \alpha \lessdot 30^{\circ}
C. 75^{\circ} \lessdot \alpha \lessdot 76^{\circ} D. 14^{\circ} \lessdot \alpha \lessdot 15^{\circ}
Zadanie 12.  1 pkt ⋅ Numer: pp-11389 ⋅ Poprawnie: 387/549 [70%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 » Podstawa trójkąta równoramiennego ma długość 12, a jego wysokość długość 8.

Oblicz długość wysokości opuszczonej na ramię tego trójkąta.

Odpowiedź:
h_c=
(wpisz dwie liczby całkowite)
Zadanie 13.  1 pkt ⋅ Numer: pp-11545 ⋅ Poprawnie: 55/150 [36%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
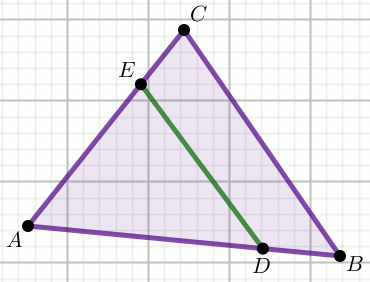
 (1 pkt) Trójkąt ABC ma pole powierzchni równe 140. Na bokach AB i AC tego trójkąta zaznaczono punkty odpowiednio D i E takie, że |DB|=\frac{3}{7}|AB| oraz |EC|=\frac{1}{5}|AC|:
Pole powierzchni trójkąta ADE jest równe:
Odpowiedzi:
A. 96 B. \frac{128}{3}
C. 48 D. 64
E. \frac{256}{5} F. \frac{256}{3}
Zadanie 14.  1 pkt ⋅ Numer: pp-11848 ⋅ Poprawnie: 161/304 [52%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
 Wysokość trójkąta równobocznego jest równa 3\sqrt{2}. Pole powierzchni tego trójkąta jest równe:
Odpowiedzi:
A. 9\sqrt{3} B. 6\sqrt{3}
C. \frac{3\sqrt{3}}{2} D. 3\sqrt{3}
E. 6 F. 18
Zadanie 15.  1 pkt ⋅ Numer: pp-12069 ⋅ Poprawnie: 42/68 [61%] Rozwiąż 
Podpunkt 15.1 (1 pkt)
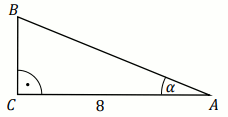
 Przyprostokątna AC trójkąta prostokątnego ABC ma długość 8 oraz \tan\alpha=\frac{3}{4} (zobacz rysunek).

Pole tego trójkąta jest równe:

Odpowiedzi:
A. 24 B. \frac{96}{7}
C. 9 D. 40
E. 6 F. 60
G. 12 H. 48
Zadanie 16.  1 pkt ⋅ Numer: pp-12070 ⋅ Poprawnie: 41/67 [61%] Rozwiąż 
Podpunkt 16.1 (1 pkt)
 Pole pewnego trójkąta równobocznego jest równe \frac{4\sqrt{3}}{9}.

Obwód tego trójkąta jest równy:

Odpowiedzi:
A. 4 B. \frac{17}{4}
C. 5 D. \frac{25}{6}
E. \frac{22}{5} F. 2\sqrt{3}
G. 4\sqrt{3} H. \frac{9}{2}
Zadanie 17.  2 pkt ⋅ Numer: pp-20745 ⋅ Poprawnie: 43/196 [21%] Rozwiąż 
Podpunkt 17.1 (2 pkt)
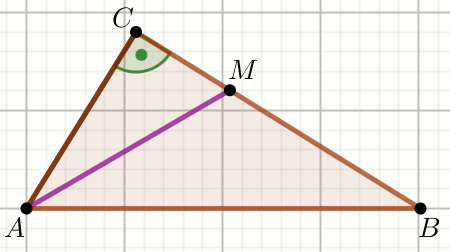
 » Odcinki AM i MB na rysunku maja równą długość, a bok AC ma długość 22:

Wiedząc, że P_{\triangle ABC}=242\sqrt{3}, oblicz P_{\triangle ABM}.

Odpowiedź:
P_{\triangle ABM}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 18.  2 pkt ⋅ Numer: pp-20746 ⋅ Poprawnie: 48/156 [30%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
 « Jeden z kątów trójkąta równoramiennego ma miarę \alpha taką, że \cos\alpha=-\frac{1}{2} a pole powierzchni tego trójkąta jest równe 225.

Oblicz \alpha.

Odpowiedź:
\alpha\ [^{\circ}]= (wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
 Oblicz długość ramienia tego trójkąta.
Odpowiedź:
c= (liczba zapisana dziesiętnie)
Zadanie 19.  2 pkt ⋅ Numer: pp-20281 ⋅ Poprawnie: 19/60 [31%] Rozwiąż 
Podpunkt 19.1 (2 pkt)
 « W okrąg o obwodzie \frac{2}{3}\pi wpisano ośmiokąt foremny.

Oblicz pole powierzchni tego ośmiokąta.

Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 20.  2 pkt ⋅ Numer: pp-20279 ⋅ Poprawnie: 104/190 [54%] Rozwiąż 
Podpunkt 20.1 (2 pkt)
 Dwa boki trójkąta mają długości \frac{4}{5} i \frac{3}{5}, a pole powierzchni tego trójkąta jest równe \frac{4}{25}.

Wyznacz z dokładnością do jednego stopnia miarę kąta zawartego między tymi bokami.

Odpowiedź:
\alpha\ [^{\circ}]= (wpisz liczbę całkowitą)
Zadanie 21.  2 pkt ⋅ Numer: pp-20284 ⋅ Poprawnie: 18/39 [46%] Rozwiąż 
Podpunkt 21.1 (2 pkt)
 » We wnętrzu trójkąta równobocznego o boku długości 5\sqrt{2} zaznaczono dowolny punkt.

Oblicz sumę odległości tego punktu od wszystkich boków tego trójkąta.

Odpowiedź:
d= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 22.  2 pkt ⋅ Numer: pp-20751 ⋅ Poprawnie: 52/141 [36%] Rozwiąż 
Podpunkt 22.1 (2 pkt)
 « Pole powierzchni trójkąta prostokątnego jest równe 24, a jeden z jego kątów ostrych spełnia warunek \tan\alpha=\frac{1}{3}.

Oblicz długość wysokości opuszczonej na przeciwprostokątna tego trójkąta.

Odpowiedź:
h= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 23.  2 pkt ⋅ Numer: pp-20749 ⋅ Poprawnie: 67/234 [28%] Rozwiąż 
Podpunkt 23.1 (2 pkt)
 « W trójkącie prostokątnym kąt ostry spałnia warunek \cos\alpha=\frac{1}{3}, a promień okręgu opisanego na tym trójkącie ma długość 10.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= (liczba zapisana dziesiętnie)
Zadanie 24.  2 pkt ⋅ Numer: pp-20750 ⋅ Poprawnie: 10/41 [24%] Rozwiąż 
Podpunkt 24.1 (2 pkt)
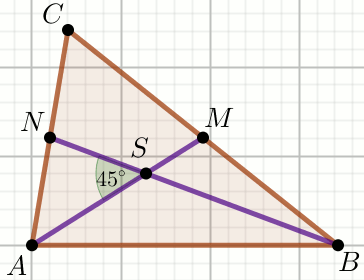
 « Punkty M i N są środkami boków trójkąta na rysunku i spełniają warunki: |AM|=18 i |BN|=\frac{63}{2}:

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle ABC}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 25.  2 pkt ⋅ Numer: pp-20901 ⋅ Poprawnie: 6/11 [54%] Rozwiąż 
Podpunkt 25.1 (2 pkt)
 « Pole powierzchni trójkąta prostokątnego jest równe 480, a tangens jednego z kątów ostrych tego trójkąta jest równy \frac{12}{5}.

Oblicz długość promienia okręgu opisanego na tym trójkącie.

Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Zadanie 26.  2 pkt ⋅ Numer: pp-20902 ⋅ Poprawnie: 33/50 [66%] Rozwiąż 
Podpunkt 26.1 (2 pkt)
 « Pole powierzchni trójkąta ABC jest równe 60. Środkowa CD ma długość 9, a sinus kąta BDC jest równy \frac{5}{9}.

Oblicz długość boku AB.

Odpowiedź:
|AB|= (wpisz liczbę całkowitą)
Zadanie 27.  2 pkt ⋅ Numer: pp-20904 ⋅ Poprawnie: 5/8 [62%] Rozwiąż 
Podpunkt 27.1 (2 pkt)
 Podstawą trójkąta równoramiennego ABC jest bok AB. Środkowe AL i BK przecinają się w punkcie S i tworzą kąt ASB o mierze 60^{\circ}. Wiadomo, że pole powierzchni trójkąta ABS jest równe 100\sqrt{3}.

Oblicz pole powierzchni trójkąta ABC.

Odpowiedź:
P_{\triangle ABC}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 28.  2 pkt ⋅ Numer: pp-21054 ⋅ Poprawnie: 307/807 [38%] Rozwiąż 
Podpunkt 28.1 (2 pkt)
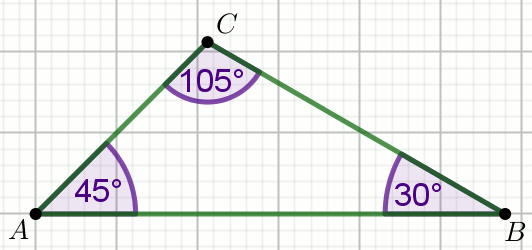
 Dany jest trójkąt, którego kąty mają miary 30^{\circ}, 45^{\circ} oraz 105^{\circ}. Długości boków tego trójkąta są równe: |AB|=5c, |BC|=b i |AC|=2a.

Oceń, które z podanych wyrażeń poprawnie określają pole tego trójkąta:

Odpowiedzi:
T/N : 5\sqrt{2}a\cdot c T/N : \frac{5}{2}b\cdot c
T/N : \frac{5}{8}b\cdot c T/N : 10\sqrt{2}a\cdot c
Zadanie 29.  2 pkt ⋅ Numer: pp-21097 ⋅ Poprawnie: 24/77 [31%] Rozwiąż 
Podpunkt 29.1 (2 pkt)
 Dany jest trójkąt ABC, w którym |AC|=3, |AB|=4 \cos\sphericalangle BAC=\frac{3}{5}.

Oblicz pole trójkąta ABC.

Odpowiedź:
P_{\triangle ABC}=
(wpisz dwie liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm