Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Pole trójkąta cz.2

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-11925 ⋅ Poprawnie: 135/226 [59%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 Pole prostokąta jest równe \frac{361}{3}, a przekątne tego prostokąta przecinają się pod kątem ostrym \alpha, takim, że \sin\alpha=\frac{1}{24}.

Długość przekątnej tego prostokąta jest równa:

Odpowiedzi:
A. 93 B. 85
C. 96 D. 76
E. 77 F. 65
Zadanie 2.  2 pkt ⋅ Numer: pp-20905 ⋅ Poprawnie: 3/99 [3%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 Pole powierzchni trójkąta równoramiennego jest równe 120, a sinus kąta kąta przy podstawie jest równy \frac{15}{17}.

Oblicz długość obwodu tego trójkąta.

Odpowiedź:
L= (wpisz liczbę całkowitą)
Podpunkt 2.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 3.  2 pkt ⋅ Numer: pp-21026 ⋅ Poprawnie: 2/92 [2%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 Pole powierzchni trójkąta równoramiennego jest równe 2640, a cosinus kąta przy podstawie jest równy \frac{48}{73}.

Oblicz długość obwodu tego trójkąta.

Odpowiedź:
L= (wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 4.  2 pkt ⋅ Numer: pp-21027 ⋅ Poprawnie: 38/64 [59%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 « Pole powierzchni trójkąta równoramiennego jest równe 3072, a tangens kąta kąta przy podstawie jest równy \frac{4}{3}.

Oblicz długość obwodu tego trójkąta.

Odpowiedź:
L= (wpisz liczbę całkowitą)
Podpunkt 4.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 5.  2 pkt ⋅ Numer: pp-20906 ⋅ Poprawnie: 23/63 [36%] Rozwiąż 
Podpunkt 5.1 (2 pkt)
 « Pole powierzchni trójkąta jest równe 84, a promień okręgu wpisanego w ten trójkąt ma długość 4.

Wiedząc, że długości boków tego trójkąta są kolejnymi liczbami naturalnymi, oblicz długość najkrótszej wysokości tego trójkąta.

Odpowiedź:
h_{min}=
(wpisz dwie liczby całkowite)
Zadanie 6.  2 pkt ⋅ Numer: pp-21028 ⋅ Poprawnie: 23/40 [57%] Rozwiąż 
Podpunkt 6.1 (2 pkt)
 « Pole powierzchni trójkąta jest równe 6, a promień okręgu wpisanego w ten trójkąt ma długość 1.

Wiedząc, że długości boków tego trójkąta są kolejnymi liczbami naturalnymi, oblicz długość najdłuższej wysokości tego trójkąta.

Odpowiedź:
h_{min}=
(wpisz dwie liczby całkowite)
Zadanie 7.  2 pkt ⋅ Numer: pp-20907 ⋅ Poprawnie: 42/115 [36%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 Podstawa trójkąta równoramiennego ma długość 16, a pole powierzchni tego trójkąta jest równe 120.

Oblicz długość ramienia tego trójkąta.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
 Wyznacz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Zadanie 8.  2 pkt ⋅ Numer: pp-21029 ⋅ Poprawnie: 16/25 [64%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 Podstawa trójkąta równoramiennego ma długość 96, a pole powierzchni tego trójkąta jest równe 2640.

Oblicz długość obwodu tego trójkąta.

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
 Wyznacz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Zadanie 9.  2 pkt ⋅ Numer: pp-20908 ⋅ Poprawnie: 38/71 [53%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 W trójkącie równoramiennym podstawa ma długość 16, a cosinus kąta przy podstawie jest równy \frac{8}{17}.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= (wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
 Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Zadanie 10.  2 pkt ⋅ Numer: pp-21030 ⋅ Poprawnie: 1/3 [33%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 W trójkącie równoramiennym podstawa ma długość 96, a sinus kąta przy podstawie jest równy \frac{55}{73}.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= (wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
 Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Zadanie 11.  2 pkt ⋅ Numer: pp-21031 ⋅ Poprawnie: 1/4 [25%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 W trójkącie równoramiennym podstawa ma długość 128, a tangens kąta przy podstawie jest równy \frac{3}{4}.

Oblicz pole powierzchni tego trójkąta.

Odpowiedź:
P_{\triangle}= (wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
 Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Zadanie 12.  2 pkt ⋅ Numer: pp-20909 ⋅ Poprawnie: 3/8 [37%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 W trójkącie dwa boki mają długość 17, a promień okręgu opisanego na tym trójkącie ma długość \frac{289}{30}. Pole powierzchni tego trójkąta jest równe 120.

Oblicz długość trzeciego boku tego trójkąta.

Odpowiedź:
c= (wpisz liczbę całkowitą)
Podpunkt 12.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 13.  2 pkt ⋅ Numer: pp-20910 ⋅ Poprawnie: 38/57 [66%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 Dwa boki trójkąta mają długość 28 i 30, a promień okręgu opisanego na tym trójkącie ma długość \frac{65}{4}. Pole powierzcni tego trójkąta jest równe 336.

Oblicz długość trzeciego boku tego trójkąta.

Odpowiedź:
c= (wpisz liczbę całkowitą)
Podpunkt 13.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 14.  2 pkt ⋅ Numer: pp-21032 ⋅ Poprawnie: 25/36 [69%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
 Dwa boki trójkąta mają długość 17 i 25, a promień okręgu opisanego na tym trójkącie ma długość \frac{325}{24}. Pole powierzcni tego trójkąta jest równe 204.

Oblicz długość trzeciego boku tego trójkąta.

Odpowiedź:
c= (wpisz liczbę całkowitą)
Podpunkt 14.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 15.  2 pkt ⋅ Numer: pp-21033 ⋅ Poprawnie: 3/3 [100%] Rozwiąż 
Podpunkt 15.1 (1 pkt)
 Dwa boki trójkąta mają długość 6 i 29, a promień okręgu opisanego na tym trójkącie ma długość \frac{145}{8}. Pole powierzcni tego trójkąta jest równe 60.

Oblicz długość trzeciego boku tego trójkąta.

Odpowiedź:
c= (wpisz liczbę całkowitą)
Podpunkt 15.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 16.  3 pkt ⋅ Numer: pp-20911 ⋅ Poprawnie: 19/37 [51%] Rozwiąż 
Podpunkt 16.1 (1 pkt)
 Dwa boki trójkąta ostrokątnego mają długość 6 i 17, a jego pole powierzchni jest równe 17.

Oblicz sinus kąta zawartego między tymi bokami.

Odpowiedź:
\sin\alpha=
(wpisz dwie liczby całkowite)
Podpunkt 16.2 (1 pkt)
 Oblicz długość trzeciego boku tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Podpunkt 16.3 (1 pkt)
 Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 17.  2 pkt ⋅ Numer: pp-20753 ⋅ Poprawnie: 55/231 [23%] Rozwiąż 
Podpunkt 17.1 (2 pkt)
 » Promień okręgu opisanego na trójkącie prostokątnym jest równy R, a promień okręgu wpisanego w ten trójkąt - r.

Oblicz pole powierzchni tego trójkąta.

Dane
R=13
r=4=4.00000000000000
Odpowiedź:
P_{\triangle}= (wpisz liczbę całkowitą)
Zadanie 18.  2 pkt ⋅ Numer: pp-20755 ⋅ Poprawnie: 46/177 [25%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
 W trójkącie równoramiennym podstawa ma długość a, a jego pole jest równe P. Promień okręgu wpisanego w ten trójkąta ma długość r.

Oblicz długość ramienia tego trójkąta.

Dane
a=20
P=240
r=\frac{20}{3}=6.66666666666667
Odpowiedź:
b= (wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
 Oblicz sinus kąta między ramionami tego trójkąta.
Odpowiedź:
\sin\alpha=
(wpisz dwie liczby całkowite)
Zadanie 19.  2 pkt ⋅ Numer: pp-20199 ⋅ Poprawnie: 63/107 [58%] Rozwiąż 
Podpunkt 19.1 (2 pkt)
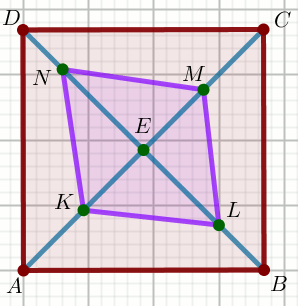
Czworokąt ABCD jest kwadratem. Punkt K jest środkiem odcinka AE, punkt M środkiem odcinka EC. Ponadto |BL|=\frac{1}{3}|BE| oraz |DN|=\frac{1}{3}|DE|.

Ile razy pole kwadratu jest większe od pola czworokąta KLMN?

Odpowiedź:
P_{\square KLMN}= (wpisz liczbę całkowitą)
Zadanie 20.  2 pkt ⋅ Numer: pp-20754 ⋅ Poprawnie: 48/117 [41%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
 « Dwa boki trójkąta mają długość a i b, a promień okręgu opisanego na tym trójkącie jest równy R. Pole powierzchni tego trójkąta jest równe P.

Wyznacz długość trzeciego boku tego trójkąta.

Dane
a=20
b=7
R=\frac{25}{2}=12.50000000000000
P=42
Odpowiedź:
c= (wpisz liczbę całkowitą)
Podpunkt 20.2 (1 pkt)
 Wyznacz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 21.  2 pkt ⋅ Numer: pp-20198 ⋅ Poprawnie: 71/181 [39%] Rozwiąż 
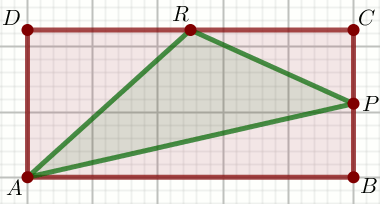
Podpunkt 21.1 (2 pkt)
W prostokącie ABCD punkt P jest środkiem boku BC, a punkt R jest środkiem boku CD.

Jakim procentem sumy pól trójkątów ARD i PCR jest pole trójkąta APR?

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 22.  2 pkt ⋅ Numer: pp-20752 ⋅ Poprawnie: 41/170 [24%] Rozwiąż 
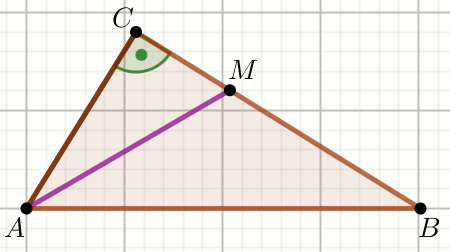
Podpunkt 22.1 (2 pkt)
 «« Odcinki AM i MB na rysunku maja równą długość:

Oblicz P_{AMC}.

Dane
|AC|=10
P_{\triangle ABC}=120=120.00000000000000
Odpowiedź:
P_{\triangle AMC}=
(wpisz dwie liczby całkowite)
Zadanie 23.  2 pkt ⋅ Numer: pp-21098 ⋅ Poprawnie: 36/110 [32%] Rozwiąż 
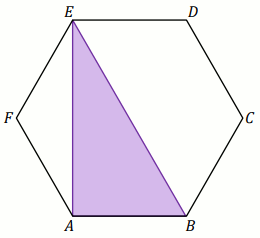
Podpunkt 23.1 (1 pkt)
 Dany jest sześciokąt foremny ABCDEF o polu równym 16\sqrt{3} (zobacz rysunek).

Pole trójkąta ABE jest równe:

Odpowiedzi:
A. \frac{64}{9} B. \frac{16\sqrt{3}}{3}
C. \frac{32\sqrt{3}}{9} D. 4\sqrt{3}
E. \frac{64}{5} F. 8\sqrt{3}
Podpunkt 23.2 (1 pkt)
 Długość odcinka AE jest równa:
Odpowiedzi:
A. 4\sqrt{2} B. 6\sqrt{2}
C. \frac{16}{3} D. \frac{16\sqrt{6}}{5}
E. 48\sqrt{2} F. \frac{8\sqrt{2}}{3}
Zadanie 24.  4 pkt ⋅ Numer: pp-30025 ⋅ Poprawnie: 38/219 [17%] Rozwiąż 
Podpunkt 24.1 (4 pkt)
 «« W trójkącie ABC dane są długości boków AC, BC i kąt między tymi bokami o mierze 60^{\circ}. Dwusieczna kąta BCA przecina bok AB w punkcie D.

Oblicz |CD|.

Dane
|AC|=6
|BC|=2
Odpowiedź:
|CD|= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 25.  4 pkt ⋅ Numer: pp-30020 ⋅ Poprawnie: 35/120 [29%] Rozwiąż 
Podpunkt 25.1 (4 pkt)
 « Każdy bok trójkąta podzielono dwoma punktami na odcinki, których długości mają się do siebie jak a:b:a. Pole powierzchni tego trójkąta jest równe P.

Wyznacz pole sześciokąta, którego wierzchołkami są punkty podziałów boków trójkąta.

Dane
a=2
b=1
P=25
Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 26.  4 pkt ⋅ Numer: pp-30398 ⋅ Poprawnie: 11/46 [23%] Rozwiąż 
Podpunkt 26.1 (1 pkt)
 « Dwa boki trójkąta ostrokątnego mają długość 14 i 15, a jego pole powierzchni jest równe \frac{105}{2}.

Oblicz miarę stopniową kąta zawartego między tymi bokami.

Odpowiedź:
\alpha= (wpisz liczbę całkowitą)
Podpunkt 26.2 (1 pkt)
 Oblicz długość trzeciego boku tego trójkąta.
Odpowiedź:
c= \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 26.3 (1 pkt)
 Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R= (liczba zapisana dziesiętnie)
Podpunkt 26.4 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
r= (liczba zapisana dziesiętnie)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm