⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Pole trójkąta cz.2
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- pole powierzchni trójkąta
- wzory ma pole trójkąta:
- P=r\cdot p
- P=\frac{a\cdot b\cdot c}{4R}
- P=\sqrt{p(p-a)(p-b)(p-c)}
- promień okręgu wpisanego: r=\frac{P}{p}
- promień okręgu opisanego: R=\frac{a\cdot b\cdot c}{4P}
| Zadanie 1. 2 pkt ⋅ Numer: pr-20749 ⋅ Poprawnie: 61/65 [93%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Oblicz długości boków trójkąta równoramiennego o polu powierzchni równym
P i kącie między ramionami o mierze
45^{\circ}.
Podaj długość ramienia tego trójkąta.
Dane
P=36\sqrt{2}=50.91168824543142
Odpowiedź:
b=
(wpisz liczbę całkowitą)
Podpunkt 1.2 (1 pkt)
Podaj długość podstawy tego trójkąta.
Odpowiedź:
a=
(liczba zapisana dziesiętnie)
| Zadanie 2. 2 pkt ⋅ Numer: pr-20568 ⋅ Poprawnie: 76/65 [116%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Dwa boki trójkąta maja długości a i
b, a jego pole powierzchni jest równe
P. W trójkąt ten wpisano okrąg o promieniu
długości r.
Wyznacz najmniejszy z sinusów kątów tego trojkąta.
Dane
a=28
b=28
r=\frac{14\sqrt{3}}{3}=8.08290376865476
P=196\sqrt{3}=339.48195828349995
b=28
r=\frac{14\sqrt{3}}{3}=8.08290376865476
P=196\sqrt{3}=339.48195828349995
Odpowiedź:
| min= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 2.2 (1 pkt)
Wyznacz największy z sinusów kątów tego trojkąta.
Odpowiedź:
| max= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. 1 pkt ⋅ Numer: pr-21159 ⋅ Poprawnie: 90/91 [98%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Dany jest trójkąt prostokątny ABC, w którym
|\sphericalangle ABC|=90^{\circ} oraz
|\sphericalangle CAB|=60^{\circ}. Punkty K i
L leżą na bokach – odpowiednio – AB i
BC tak, że |BK|=|BL|=3 (zobacz rysunek).
Odcinek KL przecina wysokość BD tego trójkąta
w punkcie N, a ponadto |AD|=16.
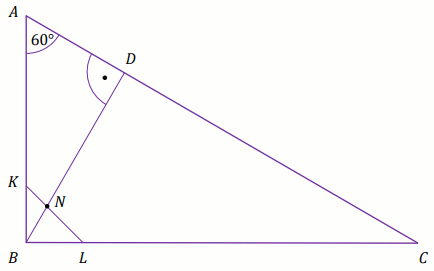
Oblicz, |ND|.
Odpowiedź:
| |ND|= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 4. 4 pkt ⋅ Numer: pr-30346 ⋅ Poprawnie: 72/65 [110%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
««« W trójkącie ABC dane są:
|\sphericalangle BCA|=120^{\circ},
|AC|=b i |BC|=a oraz
dwusieczna CD.
Oblicz |CD|.
Dane
a=4
b=10
b=10
Odpowiedź:
| |CD|= | |
Podpunkt 4.2 (2 pkt)
Oblicz długość promienia okręgu opisanego na trójkącie
DBC.
Odpowiedź:
| R_{\triangle DBC}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 4 pkt ⋅ Numer: pr-31045 ⋅ Poprawnie: 78/65 [120%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
Dany jest trójkąt prostokątny ABC. Promień okręgu wpisanego w ten
trójkąt jest równy 12 i jest o 46 krótszy od przeciwprostokątnej tego trójkąta.
Oblicz iloczyn długości przyprostokątnych tego trójkata.
Odpowiedź:
a\cdot b=
(wpisz liczbę całkowitą)
Podpunkt 5.2 (2 pkt)
Oblicz sinus większego z kątów ostrych tego trójkąta.
Odpowiedź:
| \sin\alpha= | |