Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania ☆ Zbiór zadań ☆ Rankingi ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Pola powierzchni trójkątów podobnych

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  (1 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-10587  
Podpunkt 1.1 (1 pkt)
 Trójkąty ABC i A'B'C' są podobne, a ich pola powierzchni są odpowiednio, równe 8 cm2 i 100 cm2.

Wyznacz skalę tego podobieństwa \frac{|A'B'|}{|AB|}.

Odpowiedź:
\frac{|A'B'|}{|AB|}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 2.  (1 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-10586  
Podpunkt 2.1 (1 pkt)
 « Najkrótsze wysokości dwóch trójkątów podobnych pozostają w stosunku 2:15. Pola tych trójkątów mogą być równe:
Odpowiedzi:
A. 6 i \frac{675}{2} B. 3 i \frac{225}{2}
C. 3 i \frac{45}{2} D. 1 i \frac{45}{2}
Zadanie 3.  (1 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-10591  
Podpunkt 3.1 (1 pkt)
 Trójkąt ABC jest podobny do trójkąta A_1B_1C_1 w skali k=\frac{11}{4}. Stosunek pola trójkąta ABC do pola trójkąta A_1B_1C_1 jest równy:
Odpowiedź:
\frac{P_{\triangle ABC}}{P_{\triangle A_1B_1C_1}}=
(wpisz dwie liczby całkowite)
Zadanie 7.  (2 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-20756  
Podpunkt 7.1 (2 pkt)
 « Dane są punkty na okręgu:

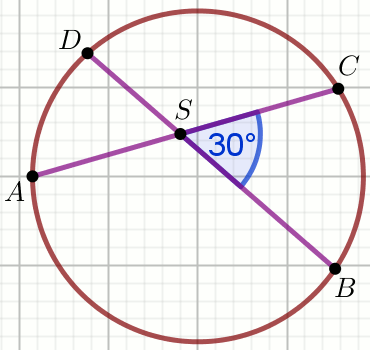
Oblicz P_{\triangle ASD}.

Dane
|AS|=16
|SB|=6
|SC|=19
Odpowiedź:
P_{\triangle ASD}=
(wpisz dwie liczby całkowite)
Zadanie 8.  (2 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-20757  
Podpunkt 8.1 (1 pkt)
 » Dany jest trójkąt równoramienny o podstawie AB:

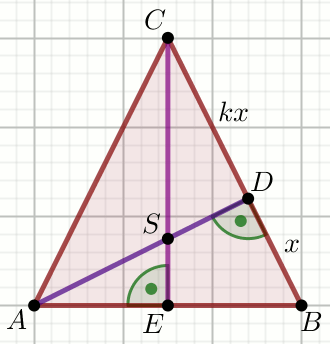
Oblicz \sin\sphericalangle DAB.

Dane
k=6
Odpowiedź:
\sin\sphericalangle DAB= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 8.2 (1 pkt)
 Oblicz \frac{P_{\triangle AES}}{P_{\triangle SDC}} .
Odpowiedź:
\frac{P_{\triangle AES}}{P_{\triangle SDC}}=
(wpisz dwie liczby całkowite)
Zadanie 9.  (2 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-20758  
Podpunkt 9.1 (2 pkt)
 « Dany jest trójkąt:

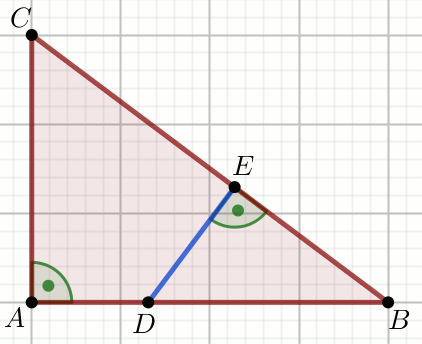
Oblicz |DE|.

Dane
|AC|=27
P_{\triangle DBE}:P_{ADEC}=98:388=0.25257731958763
Odpowiedź:
|DE|= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 10.  (2 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-20759  
Podpunkt 10.1 (2 pkt)
 Trójkąt ABC jest równoramienny o podstawie AB, a odcinek DE jest równoległy do podstawy AB:

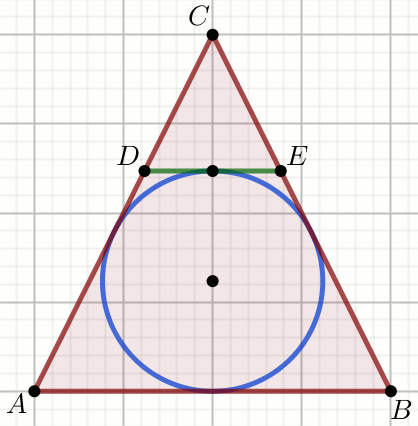
Oblicz P_{DEC}.

Dane
|AC|=|BC|=45
|AB|=54
Odpowiedź:
P_{\triangle DEC}=
(wpisz dwie liczby całkowite)
Zadanie 11.  (2 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-20760  
Podpunkt 11.1 (2 pkt)
 » Trójkąt ABC jest ostrokątny i równoramienny o podstawie AB:

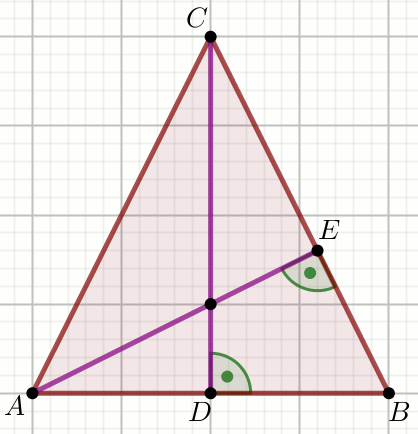
Oblicz P_{ABC}.

Dane
|AB|+|BC|+|AC|=480
\frac{P_{\triangle ABE}}{P_{\triangle ADC}}=\frac{36}{25}=1.44000000000000
Odpowiedź:
P_{\triangle ABC}= (wpisz liczbę całkowitą)
Zadanie 12.  (2 pkt) [ ⇒ Dodaj do testu ]  Numer zadania: pp-20774  
Podpunkt 12.1 (1 pkt)
 « Odcinki DE, FG i AB są równoległe, a pola wielokątów DEC, FGED i ABGF pozostają w stosunku a:b:c.

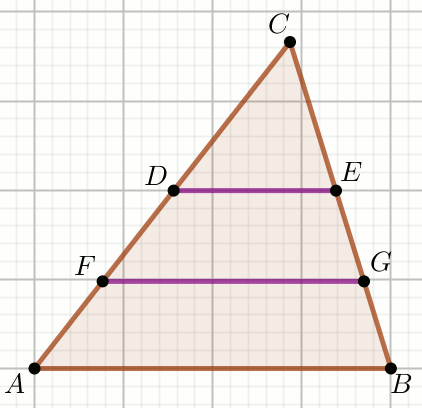
Oblicz \frac{|DE|}{|FG|}.

Dane
a=9
b=7
c=33
Odpowiedź:
\frac{|DE|}{|FG|}=
(wpisz dwie liczby całkowite)
Podpunkt 12.2 (1 pkt)
 Oblicz \frac{|FG|}{|AB|}.
Odpowiedź:
\frac{|FG|}{|AB|}=
(wpisz dwie liczby całkowite)

Liczba wyświetlonych zadań: 9

Liczba pozostałych zadań dostępnych dla zarejestrowanych nauczycieli: 8

Masz pytania? Napisz: k42195@poczta.fm