Pola trójkątów podobnych
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- trójkąty podobne
- pola powierzchni trójkątów podobnych
- stosunek pól powierzchni trójkątów podobnych
- skala podobieństwa trójkątów
| Zadanie 1. 2 pkt ⋅ Numer: pr-20946 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» W ostrokątnym trójkącie równoramiennym ABC,
|AC|=|BC|, wysokość CD przecięła
wysokość AE w punkcie S.
Wysokość AE dzieli ramię BC tego trójkąta
w stosunku |BE|:|EC|=1:2.
Oblicz sinus kąta EAB.
Odpowiedź:
| \sin\sphericalangle EAB= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 1.2 (1 pkt)
Wyznacz stosunek pola powierzchni trójkąta ADC do pola powierzchni
trójkąta CSE.
Odpowiedź:
| \frac{P_{\triangle ADC}}{P_{\triangle CSE}}}= | |
| Zadanie 2. 2 pkt ⋅ Numer: pr-20947 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (2 pkt)
Wysokość CD trójkąta ABC ma długość
4 i dzieli bok AB tego trójkąta
na odcinki o długości |AD|=8 i |DB|=18.
Poprowadzono prostą równoległą do wysokości CD, która przecięła
boki AB i BC odpowiednio w punktach
E i F.
Wiedząc, że odcinek EF dzieli trójkąt ABC na dwie figury o równych polach powierzchni, oblicz jego długość.
Odpowiedź:
| |EF|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. 3 pkt ⋅ Numer: pr-21192 ⋅ Poprawnie: 4/10 [40%] | Rozwiąż |
Podpunkt 3.1 (3 pkt)
Dany jest trójkąt ABC. Na boku AB tego trójkąta
obrano punkty D, E i F
tak, że |AD|=|DE|=|EF|=4\cdot|FB|. Na bokach AC
i BC obrano – odpowiednio – punkty G i
H tak, że DG\parallel EC oraz
FH\parallel EC (zobacz rysunek).
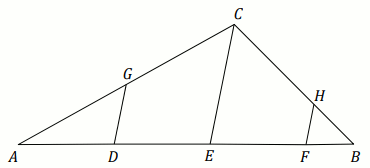

Niech pole trójkąta FBH będzie równe S.
Zapisz pole trójkąta ADG w postaci k\cdot S.
Podaj liczbę k.
Odpowiedź:
| k= | |
| Zadanie 4. 4 pkt ⋅ Numer: pr-30003 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Na bokach AB i AC trójkąta
ABC obrano punkty odpowiednio
M i L, takie, że
|MB|=2|AM| oraz |LC|=3|AL|.
Proste CM i BL przecięły
się w punkcie S. Przez punkty
A i S poprowadzono prostą,
która przecięła bok BC w punkcie
K. Pole powierzchni trójkąta
ABC jest równe 300.
Oblicz pola powierzchni trójkątów AMS,
MBS, ASL i
LSC.
Podaj najmniejsze z tych pól.
Odpowiedź:
| P_{min}= | |
Podpunkt 4.2 (2 pkt)
Podaj największe z tych pól.
Odpowiedź:
| P_{max}= | |