⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Pole wycinka i odcinka kołowego
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- pole powierzchni koła
- pole powierzchni wycinka kołowego
- pole powierzchni odcinka koła
| Zadanie 1. 1 pkt ⋅ Numer: pp-11598 ⋅ Poprawnie: 47/117 [40%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Promień koła ma długość 2, a kąt wycinka tego koła ma miarę
88^{\circ}. Oblicz pole powierzchni tego wycinka i zapisz wynik w postaci
p\cdot\pi.
Podaj liczbę p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11599 ⋅ Poprawnie: 43/82 [52%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Pole powierzchni wycinka koła jest równe 54\pi, a łuk tego wycinka ma długość
\frac{1}{7}\pi.
Oblicz długość promienia tego koła.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11600 ⋅ Poprawnie: 9/39 [23%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
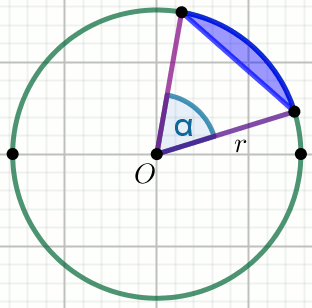
« Punkt O jest środkiem koła na rysunku, a promień r tego
koła ma długość 12. Kąt środkowy koła \alpha
oparty jest na łuku o długości 5\pi:
Oblicz pole powierzchni zaznaczonego na rysunku odcinka koła.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 1 pkt ⋅ Numer: pp-11601 ⋅ Poprawnie: 9/11 [81%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Stosunek pola powierzchni trójkąta do pola powierzchni koła wpisanego w ten trójkąt jest równy
17:\pi, a średnica tego koła ma długość 4.
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 1 pkt ⋅ Numer: pp-11602 ⋅ Poprawnie: 5/11 [45%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
W trójkącie prostokątnym stosunek długości przyprostokątnej do długości przeciwprostokątnej jest równy
8:17.
Oblicz stosunek pola powierzchni koła wpisanego w ten trójkąt do pola powierzchni koła opisanego na tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 1 pkt ⋅ Numer: pp-11699 ⋅ Poprawnie: 1/4 [25%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
W trójkącie prostokątnym stosunek długości przyprostokątnej do długości przeciwprostokątnej jest równy
20:52.
Oblicz stosunek pola powierzchni koła opisanego na tym trójkącie do pola powierzchni koła wpisanego w ten trójkąt.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 1 pkt ⋅ Numer: pp-11603 ⋅ Poprawnie: 2/13 [15%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Kąt wpisany w koło ma miarę 60^{\circ} i jest oparty
na łuku o długości 8\pi.
Oblicz pole powierzchni wycinka koła wyznaczonego przez ten łuk i zapisz wynik w postaci
p\cdot \pi.
Podaj liczbę p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20766 ⋅ Poprawnie: 19/105 [18%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
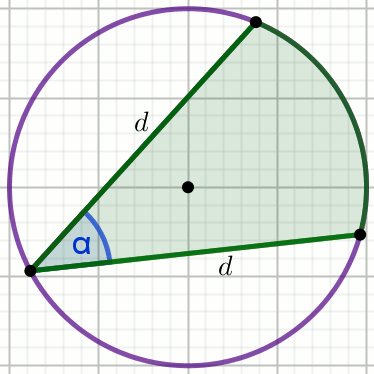
W wycinek kołowy o kącie środkowym \alpha
wpisano okrąg o polu powierzchni P:
Oblicz pole powierzchni tego wycinka.
Dane
\alpha=120^{\circ}
P=36\pi=113.09733552923256
P=36\pi=113.09733552923256
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20761 ⋅ Poprawnie: 65/212 [30%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
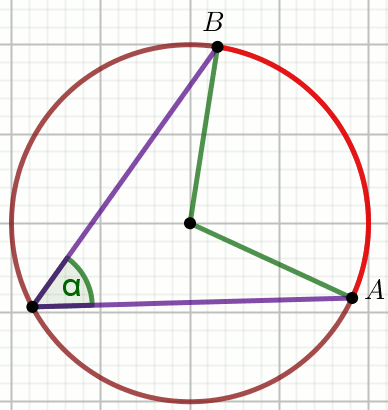
» Łuk \stackrel{\frown}{\ AB\ } ma długość
l:
Oblicz pole powierzchni wycinka kołowego wyznaczonego przez ten łuk.
Dane
l=12\pi=37.69911184307752
\alpha=15^{\circ}
\alpha=15^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20762 ⋅ Poprawnie: 25/217 [11%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
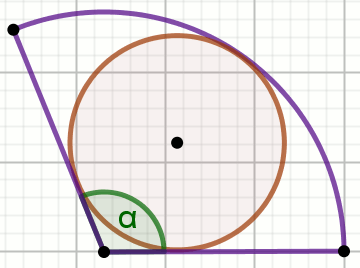
«« Dany jest okrąg:
Oblicz pole powierzchni zielonego obszaru.
Dane
d=8
\alpha=60^{\circ}
\alpha=60^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 2 pkt ⋅ Numer: pp-20763 ⋅ Poprawnie: 11/48 [22%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
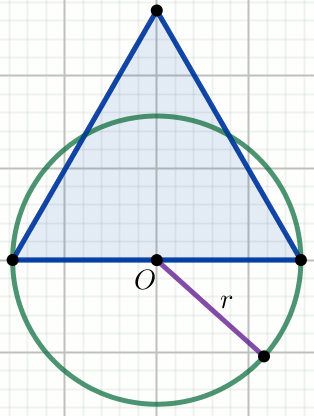
Punkt O jest środkiem okręgu, a niebieski trójkąt
jest równoboczny:
Oblicz pole powierzchni części koła leżącej poza trójkątem.
Dane
r=4\sqrt{2}=5.65685424949238
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. 2 pkt ⋅ Numer: pp-20765 ⋅ Poprawnie: 47/195 [24%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
« Punkt O jest środkiem okręgu. Oblicz pole
powierzchni niebieskiego obszaru:
Dane
r=2
\alpha=45^{\circ}
\alpha=45^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. 2 pkt ⋅ Numer: pp-20764 ⋅ Poprawnie: 18/55 [32%] | Rozwiąż |
Podpunkt 13.1 (2 pkt)
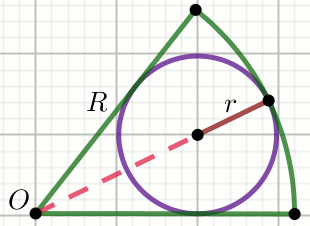
» Punkt O jest środkiem okręgu, z którego
wycięto wycinek kołowy:
Oblicz pole powierzchni tego wycinka.
Dane
r=7
R=21
R=21
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. 2 pkt ⋅ Numer: pp-20918 ⋅ Poprawnie: 2/4 [50%] | Rozwiąż |
Podpunkt 14.1 (2 pkt)
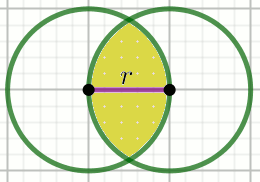
Dwa koła mają promień o długości 1 i są tak położone, że do okręgu każdego z nich
należy środek drugiego z kół:
Oblicz pole obszaru wspólnego tych kół.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. 2 pkt ⋅ Numer: pp-20919 ⋅ Poprawnie: 1/5 [20%] | Rozwiąż |
Podpunkt 15.1 (2 pkt)
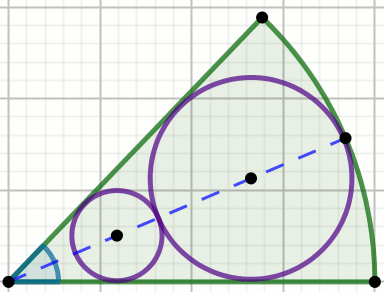
Dwa koła styczne zewnętrznie wpisano w kąt, którego miara jest równa 60^{\circ}.
Pole powierzchni mniejszego z kół jest równe 2.
Oblicz pole powierzchni większego koła.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)