Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Czworokąty - romby i równoległoboki

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-11085 ⋅ Poprawnie: 100/171 [58%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
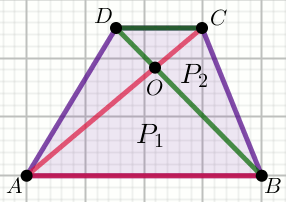
 Czworokąt na rysunku jest trapezem. Pole trójkata ABC jest równe 56, a pole trójkąta BCD jest równe 18:

Oblicz pole powierzchni tego trapezu.

Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 2.  1 pkt ⋅ Numer: pp-11474 ⋅ Poprawnie: 152/218 [69%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 W równoległoboku, z wierzchołka kąta rozwartego poprowadzono dwie wysokości tego równoległoboku, które przecięły sie pod kątem ostrym o mierze 16^{\circ}. Kąt ostry tego równoległoboku ma miarę stopniową \alpha.

Podaj \alpha.

Odpowiedź:
\alpha= (wpisz liczbę całkowitą)
Zadanie 3.  1 pkt ⋅ Numer: pp-11475 ⋅ Poprawnie: 70/97 [72%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
 « W równoległoboku kąty wewnętrzne leżące przy tym samym boku mają miary 12^{\circ} i \beta. Dwusieczne tych kątów przecinają się pod kątem o mierze stopniowej \alpha.

Podaj \alpha.

Odpowiedź:
\alpha= (wpisz liczbę całkowitą)
Zadanie 4.  1 pkt ⋅ Numer: pp-11094 ⋅ Poprawnie: 378/542 [69%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 Kąt rombu ma miarę 135^{\circ}, a jego wysokość długość 2\sqrt{2}.

Oblicz długość boku tego rombu.

Odpowiedź:
a= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 5.  1 pkt ⋅ Numer: pp-11096 ⋅ Poprawnie: 159/322 [49%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 W romb o boku długości \frac{7\sqrt{3}}{6} i kącie rozwartym 120^{\circ} wpisano okrąg.

Oblicz długość promienia tego okręgu.

Odpowiedź:
r= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 6.  1 pkt ⋅ Numer: pp-11087 ⋅ Poprawnie: 259/453 [57%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 « Przekątne rombu mają długości 2\sqrt{3} i 4\sqrt{3}.

Wyznacz obwód tego rombu.

Odpowiedź:
L= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 7.  1 pkt ⋅ Numer: pp-11100 ⋅ Poprawnie: 94/192 [48%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
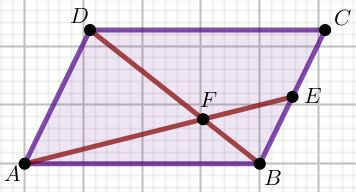
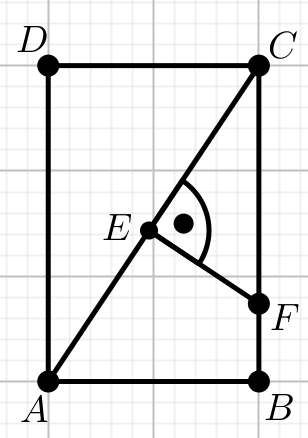
 « Czworokąt na rysunku jest równoległobokiem, w którym |FB|=2 oraz |BE|:|CE|=1:4:

Oblicz długość odcinka DF.

Odpowiedź:
|DF|=
(wpisz dwie liczby całkowite)
Zadanie 8.  1 pkt ⋅ Numer: pp-11444 ⋅ Poprawnie: 57/156 [36%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
« Punkty A, B, C nie leżą na jednej prostej i wraz z punktem D są wierzchołkami równoległoboku.

Ile jest takich figur?

Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Zadanie 9.  1 pkt ⋅ Numer: pp-11480 ⋅ Poprawnie: 18/50 [36%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
 Przekątne rombu maja długości 3\sqrt{3} i 4\sqrt{3}.

Oblicz obwód tego rombu.

Odpowiedź:
L= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 10.  1 pkt ⋅ Numer: pp-11101 ⋅ Poprawnie: 93/203 [45%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
 « W równoległoboku ABCD o krótszym boku długości 3, kąt przy wierzchołku D jest rozwarty. Punkt H jest punktem wspólnym dwusiecznej tego kąta i boku AB i spełnia warunek |HB|:|AH|=2:9.

Wyznacz obwód tego równoległoboku.

Odpowiedź:
L=
(wpisz dwie liczby całkowite)
Zadanie 11.  1 pkt ⋅ Numer: pp-11091 ⋅ Poprawnie: 89/147 [60%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 W rombie ABCD cosinus kąta rozwartego jest równy -\frac{\sqrt{2}}{4}.

Oblicz cosinus kąta ostrego tego rombu.

Odpowiedź:
\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 12.  1 pkt ⋅ Numer: pp-11772 ⋅ Poprawnie: 504/695 [72%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 W rombie o boku długości 5\sqrt{3} kąt rozwarty ma miarę 150^{\circ}.

Iloczyn długości przekątnych tego rombu jest równy:

Odpowiedzi:
A. 37 B. 75
C. 150 D. 75\sqrt{3}
Zadanie 13.  1 pkt ⋅ Numer: pp-12039 ⋅ Poprawnie: 12/33 [36%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 W romb o boku 9\sqrt{5} i kącie 60^{\circ} wpisano okrąg.

Promień tego okręgu jest równy:

Odpowiedzi:
A. \frac{9\sqrt{30}}{4} B. \frac{9\sqrt{15}}{4}
C. 9\sqrt{15} D. \frac{9\sqrt{30}}{8}
E. \frac{27\sqrt{5}}{8} F. \frac{9\sqrt{15}}{2}
Zadanie 14.  1 pkt ⋅ Numer: pp-12073 ⋅ Poprawnie: 17/23 [73%] Rozwiąż 
Podpunkt 14.1 (1 pkt)
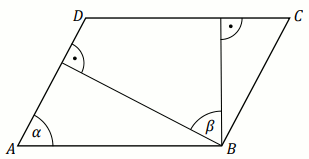
 W równoległoboku ABCD, przedstawionym na rysunku, kąt \alpha ma miarę 68^{\circ}.

Wtedy kąt \beta ma miarę:

Odpowiedzi:
A. 67^{\circ} B. 74^{\circ}
C. 68^{\circ} D. 65^{\circ}
E. 64^{\circ} F. 63^{\circ}
G. 66^{\circ} H. 62^{\circ}
Zadanie 15.  2 pkt ⋅ Numer: pp-20443 ⋅ Poprawnie: 18/96 [18%] Rozwiąż 
Podpunkt 15.1 (2 pkt)
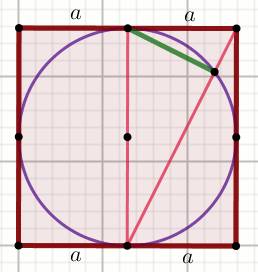
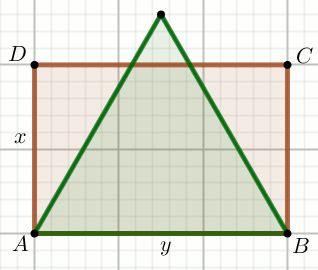
 « Czworokąt na rysunku jest kwadratem, w którym a=5:

Oblicz długość zielonego odcinka.

Odpowiedź:
Wpisz odpowiedź:  \cdot√
(wpisz dwie liczby całkowite)
Zadanie 16.  2 pkt ⋅ Numer: pp-20444 ⋅ Poprawnie: 18/95 [18%] Rozwiąż 
Podpunkt 16.1 (2 pkt)
 Czworokąt ABCD na rysunku jest prostokątem, a zielony trójkąt jest równoboczny, przy czym x=12 i y=16:

Oblicz długość boku DC prostokąta, zawartego wewnątrz zielonego trójkąta.

Odpowiedź:
d= + \cdot√
(wpisz cztery liczby całkowite)
Zadanie 17.  2 pkt ⋅ Numer: pp-20445 ⋅ Poprawnie: 67/233 [28%] Rozwiąż 
Podpunkt 17.1 (1 pkt)
 « Kąt rozwarty rombu ma miarę 120^{\circ}, a jego wysokość jest równa 4.

Oblicz obwód tego rombu.

Odpowiedź:
L= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 17.2 (1 pkt)
 Oblicz długość krótszej przekątnej tego rombu.
Odpowiedź:
d_{min}= (liczba zapisana dziesiętnie)
Zadanie 18.  2 pkt ⋅ Numer: pp-20446 ⋅ Poprawnie: 50/151 [33%] Rozwiąż 
Podpunkt 18.1 (1 pkt)
 « W rombie o boku długości 53 różnica długości jego przekątnych wynosi 34.

Oblicz długość krótszej przekątnej tego równoległoboku.

Odpowiedź:
d_{min}= (wpisz liczbę całkowitą)
Podpunkt 18.2 (1 pkt)
 Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
d_{max}= (wpisz liczbę całkowitą)
Zadanie 19.  2 pkt ⋅ Numer: pp-20447 ⋅ Poprawnie: 126/417 [30%] Rozwiąż 
Podpunkt 19.1 (1 pkt)
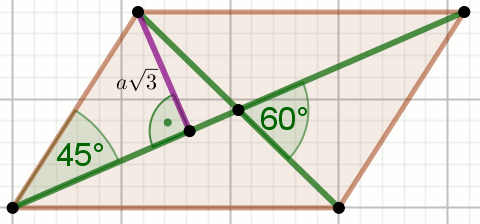
 » Czworokąt na rysunku jest równoległobokiem, przy czym a=3:
Oblicz długość krótszej przekątnej tego rombu.
Odpowiedź:
Wpisz odpowiedź:  (wpisz liczbę całkowitą)
Podpunkt 19.2 (1 pkt)
 Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
d_{max}= + \cdot √
(wpisz trzy liczby całkowite)
Zadanie 20.  2 pkt ⋅ Numer: pp-20448 ⋅ Poprawnie: 44/129 [34%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
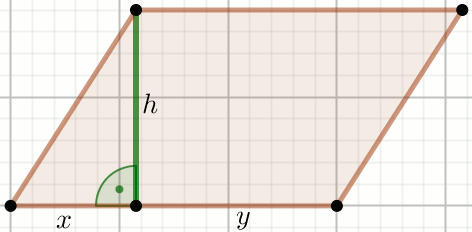
 Czworokąt na rysunku jest równoległobokiem, w którym x=27, y=50 i h=36:

Oblicz długość krótszej przekątnej tego równoległoboku.

Odpowiedź:
d_{min}= \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 20.2 (1 pkt)
 Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
d_{max}= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 21.  2 pkt ⋅ Numer: pp-20449 ⋅ Poprawnie: 54/131 [41%] Rozwiąż 
Podpunkt 21.1 (2 pkt)
 Miary kątów równoległoboku mają się do siebie jak 2:7.

Oblicz miarę stopniową kąta pod jakim przecinają się wysokości tego równoległoboku opuszczone z kąta rozwartego tego równoległoboku.

Odpowiedź:
\alpha= (wpisz liczbę całkowitą)
Zadanie 22.  2 pkt ⋅ Numer: pp-20450 ⋅ Poprawnie: 26/165 [15%] Rozwiąż 
Podpunkt 22.1 (1 pkt)
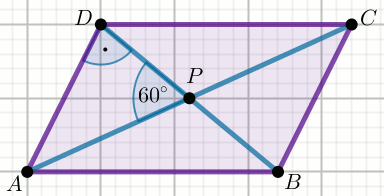
 « Czworokąt na rysunku jest równoległobokiem, w którym: |AC|=6:

Oblicz krótszy bok tego równoległoboku.

Odpowiedź:
a_{min}= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 22.2 (1 pkt)
 Oblicz dłuższy bok tego równoległoboku.
Odpowiedź:
a_{max}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 23.  2 pkt ⋅ Numer: pp-20451 ⋅ Poprawnie: 31/85 [36%] Rozwiąż 
Podpunkt 23.1 (2 pkt)
 Przekątne prostokąta mają długość 16 i przecinają sie w punkcie E oraz |EF|=6.

Oblicz długość odcinka BF.

Odpowiedź:
|BF|=
(wpisz dwie liczby całkowite)
Zadanie 24.  2 pkt ⋅ Numer: pp-21096 ⋅ Poprawnie: 13/82 [15%] Rozwiąż 
Podpunkt 24.1 (2 pkt)
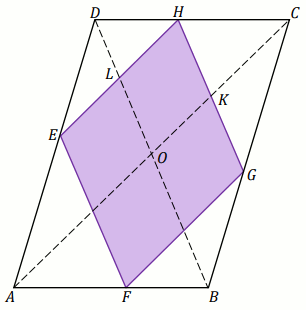
 Przekątne równoległoboku ABCD mają długość: |AC|=72, oraz |BD|=54, Wierzchołki E, F𝐹, G oraz H rombu EFGH leżą na bokach równoległoboku ABCD. Boki tego rombu są równoległe do przekątnych równoległoboku (zobacz rysunek).

Oblicz długość boku rombu EFGH.

Oblicz długość odcinka BF.

Odpowiedź:
|EF|=|FG|=
(wpisz dwie liczby całkowite)
Zadanie 25.  4 pkt ⋅ Numer: pp-30112 ⋅ Poprawnie: 18/100 [18%] Rozwiąż 
Podpunkt 25.1 (4 pkt)
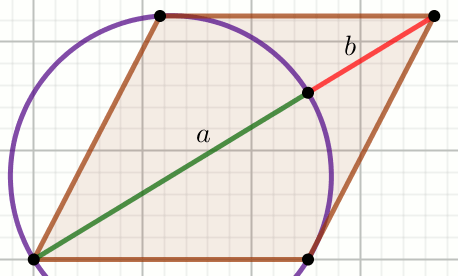
 « Czworokąt na rysunku jest rombem, w którym a=8 oraz b=4:

Oblicz długość boku tego rombu.

Odpowiedź:
a= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 26.  4 pkt ⋅ Numer: pp-30113 ⋅ Poprawnie: 89/273 [32%] Rozwiąż 
Podpunkt 26.1 (2 pkt)
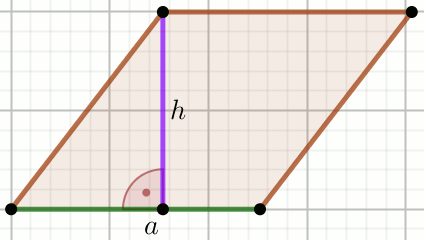
 « Czworokąt na rysunku jest rombem, w którym a=10 i h=8:

Podaj długość krótszej przekątnej tego rombu.

Odpowiedź:
d_{min}= \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 26.2 (2 pkt)
 Podaj długość dłuższej przekątnej tego rombu.
Odpowiedź:
d_{max}= \cdot√
(wpisz dwie liczby całkowite)
Zadanie 27.  4 pkt ⋅ Numer: pp-30114 ⋅ Poprawnie: 14/97 [14%] Rozwiąż 
Podpunkt 27.1 (2 pkt)
 W romb o kącie ostrym o mierze 30{^\circ} wpisano koło o polu powierzchni \frac{4}{9}\pi.

Oblicz obwód tego rombu.

Odpowiedź:
L= + \cdot√
(wpisz cztery liczby całkowite)
Podpunkt 27.2 (2 pkt)
 Oblicz długośc dłuższej przekatnej tego rombu.
Odpowiedź:
d_{max}= (liczba zapisana dziesiętnie)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm