⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Czworokąty - okrąg opisany na czworokącie
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- czworokąty
- okrąg opisany na czworokącie
- warunek opisania okręgu na czworokącie
| Zadanie 1. 2 pkt ⋅ Numer: pr-20126 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 1.1 (2 pkt)
« Trapez ABCD o krótszej podstawie |CD|=2
wpisany jest w półkole o promieniu r=16:
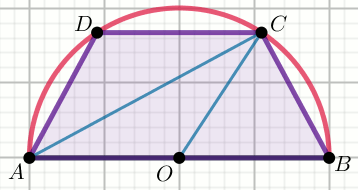
Oblicz |AC|.
Odpowiedź:
|AC|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 2. 2 pkt ⋅ Numer: pr-20127 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (2 pkt)
» Przedstawiony na rysunku czworokąt jest trapezem wpisanym w okrąg o środku
O i promieniu długości \frac{13}{2},
w którym przekątna ma długość 12:
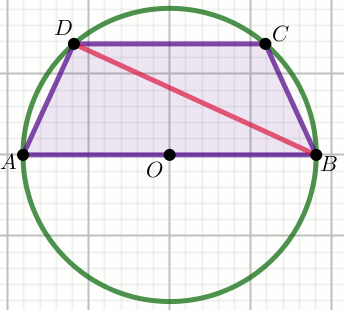
Oblicz obwód tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pr-20128 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (2 pkt)
« Na czworokącie ABCD, w którym |BC|=2 i
|CD|=1, opisano okrąg:
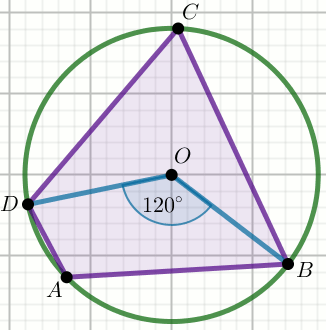
Oblicz długość promienia tego okręgu.
Odpowiedź:
R=
(wpisz liczbę całkowitą)
| Zadanie 4. 2 pkt ⋅ Numer: pr-20129 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (2 pkt)
Dany jest czworokąt wpisany w okrąg:
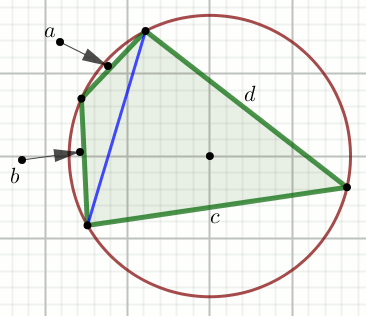
Oblicz długość niebieskiego odcinka.
Dane
a=2
b=3
c=4
d=5
b=3
c=4
d=5
Odpowiedź:
| d= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 2 pkt ⋅ Numer: pr-20130 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (2 pkt)
Dany jest czworokąt:
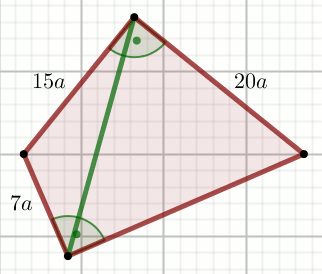
Oblicz długość zielonego odcinka.
Dane
a=1
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pr-20131 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 6.1 (2 pkt)
« Dany jest czworokąt:
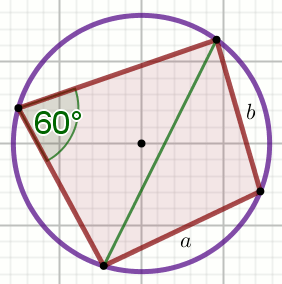
Oblicz długość zielonego odcinka.
Dane
a=16
b=14
b=14
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pr-20132 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Dany jest czworokąt:
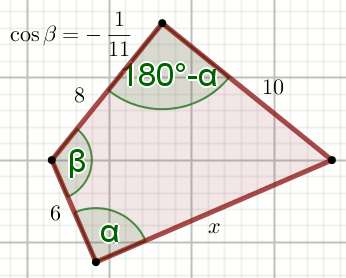
Oblicz x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20133 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (2 pkt)
Dane są figury:
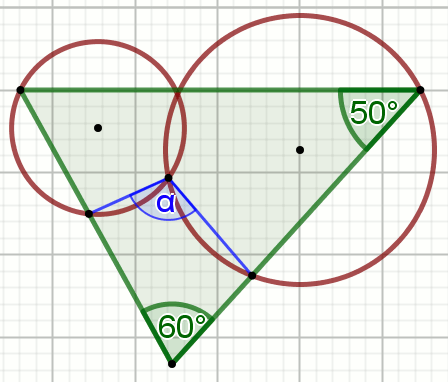
Oblicz \alpha.
Odpowiedź:
\alpha=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pr-20134 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 9.1 (2 pkt)
» Czworokąt na rysunku ma dwa kąty proste:
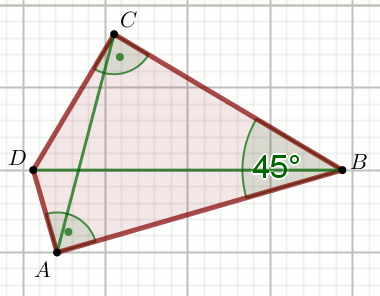
Oblicz \frac{|AC|}{|BD|}.
Odpowiedź:
| \frac{|AC|}{|BD|}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 10. 4 pkt ⋅ Numer: pr-30101 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 10.1 (4 pkt)
« Kąt rozwarty trapezu równoramiennego ABCD
o ramieniu AD ma miarę
\alpha, a jego dłuższą podstawą
jest odcinek AB. Oblicz długość promienia
okręgu opisanego na trapezie ABCD.
Podaj długość tego promienia.
Dane
|AB|=84\sqrt{3}=145.49226783578569
|AD|=6
\alpha=150^{\circ}
|AD|=6
\alpha=150^{\circ}
Odpowiedź:
R=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 11. 4 pkt ⋅ Numer: pr-30102 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 11.1 (4 pkt)
« Czworokąt na rysunku jest trapezem równoramiennym:
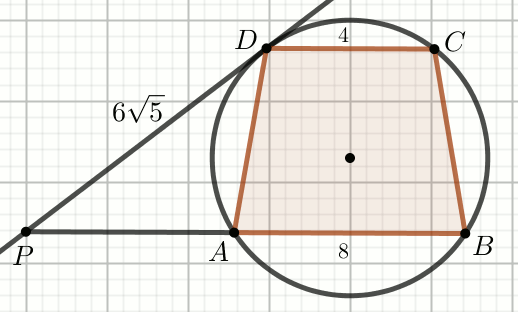
Oblicz długość promienia okręgu.
Odpowiedź:
R=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 12. 5 pkt ⋅ Numer: pr-30887 ⋅ Poprawnie: 0/8 [0%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
Czworokąt wypukły ABCD jest wpisany w okrąg o promieniu
36. Kąty BAD i BCD
są proste (zobacz rysunek).
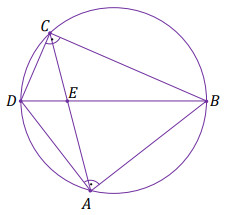
Przekątne AC i BD tego czworokąta
przecinają się w punkcie E tak, że
|BE|=7\cdot |DE| oraz |BD|=2\cdot |AE|.
Oblicz długość boku AB.
Odpowiedź:
| |AB|= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 12.2 (1 pkt)
Oblicz długość boku AD.
Odpowiedź:
| |AD|= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 12.3 (2 pkt)
Oblicz długość boku BC.
Odpowiedź:
| |BC|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 13. 2 pkt ⋅ Numer: pr-30896 ⋅ Poprawnie: 10/29 [34%] | Rozwiąż |
Podpunkt 13.1 (2 pkt)
W okrąg o promieniu 22 wpisano trójkąt ABC.
Długość boku AB jest równa 2.
Bok BC ma długość 22\sqrt{3} i jest
najdłuższym bokiem tego trójkąta.
Oblicz długość boku AC trójkąta ABC. Jeśli zadanie posiada dwa rozwiązania podaj większe z nich.
Odpowiedź:
| |AC|= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 14. 4 pkt ⋅ Numer: pr-31033 ⋅ Poprawnie: 8/18 [44%] | Rozwiąż |
Podpunkt 14.1 (2 pkt)
Czworokąt ABCD jest wpisany w okrąg o promieniu
R=6\sqrt{2}. Przekątna BD tego czworokąta ma
długość 6\sqrt{6}. Kąty wewnętrzne BAD i
ADC czworokąta ABCD są ostre, a iloczyn sinusów
wszystkich jego kątów wewnętrznych jest równy
\frac{9}{16}.
Podaj miarę stopniową kąta BCD.
Odpowiedź:
|\sphericalangle BCD| \ [^{\circ}]=
(wpisz liczbę całkowitą)
Podpunkt 14.2 (2 pkt)
Podaj miarę stopniową kąta CDA.
Odpowiedź:
|\sphericalangle CDA| \ [^{\circ}]=
(wpisz liczbę całkowitą)