Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Pole powierzchni rombu i równoległoboku

Zadania dla liceum ogólnokształcącego - poziom podstawowy

 

Zadanie 1.  1 pkt ⋅ Numer: pp-11103 ⋅ Poprawnie: 263/425 [61%] Rozwiąż 
Podpunkt 1.1 (1 pkt)
 « Kąt rozwarty rombu ma miarę 135^{\circ}. Obwód tego rombu ma długość 2\sqrt{2}.

Oblicz pole powierzchni tego rombu.

Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 2.  1 pkt ⋅ Numer: pp-11489 ⋅ Poprawnie: 162/205 [79%] Rozwiąż 
Podpunkt 2.1 (1 pkt)
 Przekątne rombu mają długości 6 i 8.

Oblicz pole powierzchni P i obwód L tego rombu.

Odpowiedzi:
P= (wpisz liczbę całkowitą)
L= (wpisz liczbę całkowitą)
Zadanie 3.  1 pkt ⋅ Numer: pp-11105 ⋅ Poprawnie: 69/154 [44%] Rozwiąż 
Podpunkt 3.1 (1 pkt)
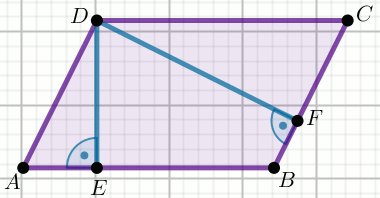
 « W równoległoboku ABCD punkt E jest środkiem boku AB.

Oblicz pole trójkąta DEC.

Dane
|AB|=4
|BC|=2
|DE|=2
Odpowiedź:
P_{\triangle DEC}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 4.  1 pkt ⋅ Numer: pp-11107 ⋅ Poprawnie: 109/192 [56%] Rozwiąż 
Podpunkt 4.1 (1 pkt)
 « W równoległoboku przekątne mają długości d i e, zaś kąt między przekątnymi ma miarę 30^{\circ}.

Oblicz pole powierzchni tego równoległoboku.

Dane
d=\frac{\sqrt{2}}{2}=0.70710678118655
e=7
Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 5.  1 pkt ⋅ Numer: pp-11446 ⋅ Poprawnie: 175/305 [57%] Rozwiąż 
Podpunkt 5.1 (1 pkt)
 « W równoległoboku przekątne mają długości d i e, zaś kąt między przekątnymi ma miarę 60^{\circ}.

Oblicz pole powierzchni tego równoległoboku.

Dane
d=\frac{\sqrt{2}}{2}=0.70710678118655
e=7
Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 6.  1 pkt ⋅ Numer: pp-11093 ⋅ Poprawnie: 197/253 [77%] Rozwiąż 
Podpunkt 6.1 (1 pkt)
 » Koło K ma promień r, trójkąt równoboczny T ma bok długości a, trójkąt P ma boki 3,4,5, zaś romb R ma obwód L i kąt ostry 45^{\circ}.

Wskaż tą figurę, która ma największe pole powierzchni:

Dane
r=2\sqrt{2}=2.82842712474619
a=5\sqrt{2}=7.07106781186548
L=16
Odpowiedzi:
A. R B. P
C. K D. T
Zadanie 7.  1 pkt ⋅ Numer: pp-11104 ⋅ Poprawnie: 213/276 [77%] Rozwiąż 
Podpunkt 7.1 (1 pkt)
 « Dany jest romb o polu powierzchni równym 40. Przekątne tego rombu spełniają warunek: \frac{|BD|}{|AC|}=\frac{4}{5}.

Oblicz |BD|.

Odpowiedź:
|BD|= (wpisz liczbę całkowitą)
Zadanie 8.  1 pkt ⋅ Numer: pp-11495 ⋅ Poprawnie: 161/229 [70%] Rozwiąż 
Podpunkt 8.1 (1 pkt)
 W pewnym równoległoboku o polu równym 209cm2 wysokość jest o 8cm krótsza od długości boku, a, na który ta wysokość jest opuszczona.

Wyznacz długość boku a tego równoległoboku.

Odpowiedź:
a= (wpisz liczbę całkowitą)
Zadanie 9.  1 pkt ⋅ Numer: pp-11796 ⋅ Poprawnie: 528/774 [68%] Rozwiąż 
Podpunkt 9.1 (1 pkt)
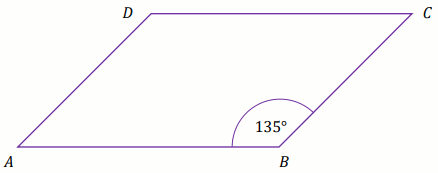
 Pole równoległoboku ABCD jest równe 1292. Bok AD tego równoległoboku ma długość 38, a kąt ABC równoległoboku ma miarę 135^{\circ} (zobacz rysunek).

Długość boku AB jest równa:

Odpowiedzi:
A. 68\sqrt{2} B. 68
C. 34 D. 17\sqrt{2}
E. 34\sqrt{6} F. 34\sqrt{2}
Zadanie 10.  1 pkt ⋅ Numer: pp-11846 ⋅ Poprawnie: 378/619 [61%] Rozwiąż 
Podpunkt 10.1 (1 pkt)
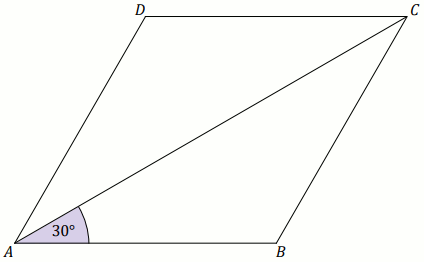
 W rombie ABCD dłuższa przekątna AC ma długość 4 i tworzy z bokiem AB kąt o mierze 30^{\circ} (zobacz rysunek).

Pole rombu ABCD jest równe:

Odpowiedzi:
A. \frac{8}{3} B. \frac{16\sqrt{3}}{3}
C. \frac{8\sqrt{3}}{3} D. \frac{8}{3}
E. 8 F. \frac{4\sqrt{3}}{3}
Zadanie 11.  1 pkt ⋅ Numer: pp-11871 ⋅ Poprawnie: 133/173 [76%] Rozwiąż 
Podpunkt 11.1 (1 pkt)
 Boki równoległoboku mają długości 7 i 8, a kąt rozwarty między tymi bokami ma miarę 120^{\circ}. Pole powierzchni tego równoległoboku jest równe:
Odpowiedzi:
A. \frac{28\sqrt{3}}{3} B. 14\sqrt{3}
C. 28\sqrt{3} D. 42\sqrt{3}
E. \frac{112\sqrt{3}}{5} F. 56\sqrt{3}
Zadanie 12.  1 pkt ⋅ Numer: pp-11894 ⋅ Poprawnie: 110/145 [75%] Rozwiąż 
Podpunkt 12.1 (1 pkt)
 Pole rombu o obwodzie 8 i kącie rozwartym 120^{\circ} jest równe:
Odpowiedzi:
A. 6 B. 2
C. 4\sqrt{3} D. \sqrt{3}
E. 2\sqrt{3} F. \frac{4\sqrt{3}}{3}
Zadanie 13.  1 pkt ⋅ Numer: pp-11995 ⋅ Poprawnie: 349/498 [70%] Rozwiąż 
Podpunkt 13.1 (1 pkt)
 Dany jest równoległobok o bokach długości 2 i 6 oraz o kącie między nimi o mierze 150^{\circ}.

Pole powierzchni tego równoległoboku jest równe:

Odpowiedzi:
A. \frac{15}{2} B. 8
C. \frac{18}{5} D. 6
E. 4 F. 3
Zadanie 14.  2 pkt ⋅ Numer: pp-20456 ⋅ Poprawnie: 57/163 [34%] Rozwiąż 
Podpunkt 14.1 (2 pkt)
 « Różnica długości przekątnych rombu wynosi 142, a bok tego rombu ma długość 85.

Oblicz pole powierzchni tego rombu.

Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 15.  2 pkt ⋅ Numer: pp-20463 ⋅ Poprawnie: 22/111 [19%] Rozwiąż 
Podpunkt 15.1 (2 pkt)
 « W romb o kącie ostrym \alpha wpisano koło. Stosunek pola powierzchni rombu do pola powerzchni koła wpisanego w ten romb wynosi p:\pi.

Oblicz \cos \alpha.

Dane
p=8
Odpowiedź:
\cos\alpha= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 16.  2 pkt ⋅ Numer: pp-20464 ⋅ Poprawnie: 17/136 [12%] Rozwiąż 
Podpunkt 16.1 (2 pkt)
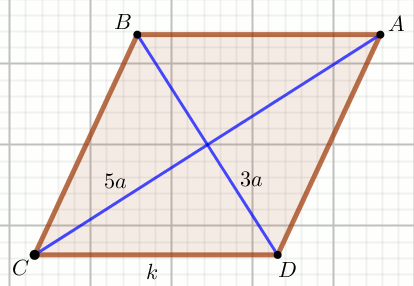
 » Czworokąt na rysunku jest rombem:

Wyznacz najmniejszą możliwą całkowitą długość krótszej przekątnej, dla której pole powierzchni tego rombu jest większe niż k.

Dane
k=39
Odpowiedź:
min= (wpisz liczbę całkowitą)
Zadanie 17.  2 pkt ⋅ Numer: pp-20465 ⋅ Poprawnie: 13/76 [17%] Rozwiąż 
Podpunkt 17.1 (1 pkt)
 » Dany jest czworokąt:

Oblicz \cos \sphericalangle CAB.

Dane
|CA|=280
|BD|=102
Odpowiedź:
\cos\sphericalangle CAB=
(wpisz dwie liczby całkowite)
Podpunkt 17.2 (1 pkt)
 Oblicz długość promienia okręgu wpisanego w ten czworokąt.
Odpowiedź:
r=
(wpisz dwie liczby całkowite)
Zadanie 18.  2 pkt ⋅ Numer: pp-20466 ⋅ Poprawnie: 30/90 [33%] Rozwiąż 
Podpunkt 18.1 (2 pkt)
 « Pole powierzchni rombu wynosi P, zaś suma kwadratów długości jego przekątnych jest równa k.

Oblicz sumę długości przekątnych tego rombu.

Dane
P=14280
k=88804
Odpowiedź:
d_1+d_2= (wpisz liczbę całkowitą)
Zadanie 19.  2 pkt ⋅ Numer: pp-20467 ⋅ Poprawnie: 36/147 [24%] Rozwiąż 
Podpunkt 19.1 (2 pkt)
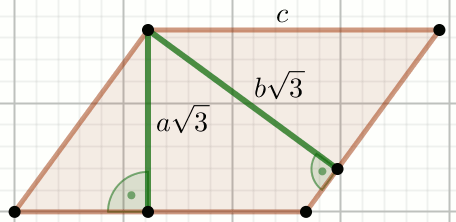
 » Czworokąt na rysunku jest rombem.

Oblicz jego pole powierzchni.

Dane
k=34
Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 20.  2 pkt ⋅ Numer: pp-20468 ⋅ Poprawnie: 36/90 [40%] Rozwiąż 
Podpunkt 20.1 (1 pkt)
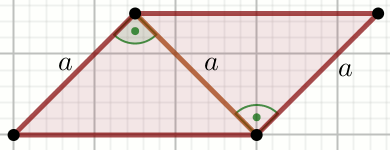
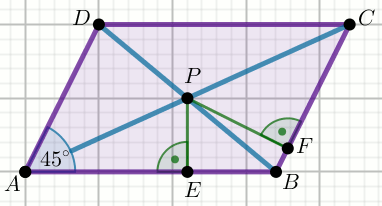
 « Czworokąt na rysunku jest równoległobokiem:

Oblicz cosinus kąta ostrego tego równoległoboku.

Dane
a=4
b=6
c=12
Odpowiedź:
\cos\alpha=
(wpisz dwie liczby całkowite)
Podpunkt 20.2 (1 pkt)
 Oblicz obwód tego równoległoboku.
Odpowiedź:
L= (wpisz liczbę całkowitą)
Zadanie 21.  2 pkt ⋅ Numer: pp-20469 ⋅ Poprawnie: 25/115 [21%] Rozwiąż 
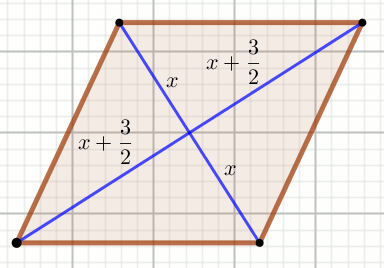
Podpunkt 21.1 (2 pkt)
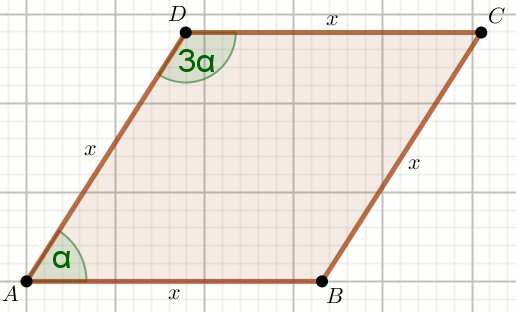
 » Czworokąt na rysunku jest równoległobokiem:

Oblicz x.

Dane
P_{ABCD}=1
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 22.  2 pkt ⋅ Numer: pp-20470 ⋅ Poprawnie: 25/115 [21%] Rozwiąż 
Podpunkt 22.1 (2 pkt)
 Równoległobok ma obwód o długości L cm, a jego wysokości mają długości h_1 cm i h_2 cm.

Oblicz pole powierzchni tego równoległoboku.

Dane
L=43
h_1=10
h_2=\frac{3}{4}=0.75000000000000
Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 23.  2 pkt ⋅ Numer: pp-20457 ⋅ Poprawnie: 33/96 [34%] Rozwiąż 
Podpunkt 23.1 (2 pkt)
 Czworokąt na rysunku jest równoległobokiem:

Oblicz pole powierzchni tego równoległoboku.

Dane
a=\frac{19\sqrt{2}}{2}=13.43502884254440
Odpowiedź:
P=
(wpisz dwie liczby całkowite)
Zadanie 24.  2 pkt ⋅ Numer: pp-20458 ⋅ Poprawnie: 153/449 [34%] Rozwiąż 
Podpunkt 24.1 (2 pkt)
 W równoległoboku dane są: |DE|=16 i |DF|=\frac{168}{5}, a obwód tego równoległogoku ma długość 124:

Oblicz jego pole powierzchni.

Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 25.  2 pkt ⋅ Numer: pp-20459 ⋅ Poprawnie: 84/136 [61%] Rozwiąż 
Podpunkt 25.1 (1 pkt)
 W równoległoboku o obwodzie 84 stosunek wysokości jest równy |DE|:|DF|=1:6:

Oblicz długość krótszego boku tego równoległoboku.

Odpowiedź:
min= (wpisz liczbę całkowitą)
Podpunkt 25.2 (1 pkt)
 Oblicz długość dłuższego boku tego równoległoboku.
Odpowiedź:
max= (wpisz liczbę całkowitą)
Zadanie 26.  2 pkt ⋅ Numer: pp-20460 ⋅ Poprawnie: 11/86 [12%] Rozwiąż 
Podpunkt 26.1 (2 pkt)
 » Czworokąt na rysunku jest równoległobokiem, w którym |PE|=2 i |PF|=2\sqrt{2}:

Oblicz jego pole powierzchni.

Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 27.  2 pkt ⋅ Numer: pp-20461 ⋅ Poprawnie: 18/84 [21%] Rozwiąż 
Podpunkt 27.1 (1 pkt)
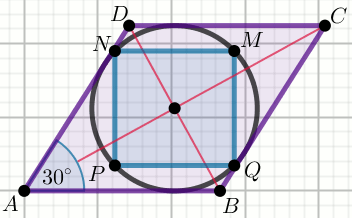
 «« W romb ABCD o kącie ostrym 30^{\circ} i boku długości |AB|=20, wpisano okrąg, w który następnie wpisano kwadrat PQMN:

Obwód tego okręgu jest równy p\cdot \pi. Wyznacz liczbę p.

Odpowiedź:
p= (wpisz liczbę całkowitą)
Podpunkt 27.2 (1 pkt)
 Oblicz \frac{P_{PQMN}}{P_{ABCD}}
Odpowiedź:
\frac{P_{PQMN}}{P_{ABCD}}=
(wpisz dwie liczby całkowite)
Zadanie 28.  2 pkt ⋅ Numer: pp-20462 ⋅ Poprawnie: 4/72 [5%] Rozwiąż 
Podpunkt 28.1 (1 pkt)
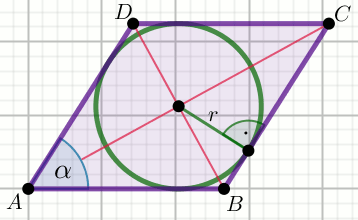
 » W romb o boku |AB|=4\sqrt{3} wpisano koło o promieniu długości r. Stosunek pola powierzchni koła wpisanego do pola powierzchni tego rombu jest równy \frac{\pi\cdot r^2}{P_{ABCD}}=\frac{\sqrt{3}}{8}\pi:

Pole powierzchni koła wpisanego w ten romb jest równe p\cdot \pi. Podaj liczbę p.

Odpowiedź:
p=
(wpisz dwie liczby całkowite)
Podpunkt 28.2 (1 pkt)
 Oblicz \cos\alpha.
Odpowiedź:
\cos\alpha=
(wpisz dwie liczby całkowite)
Zadanie 29.  4 pkt ⋅ Numer: pp-30118 ⋅ Poprawnie: 72/128 [56%] Rozwiąż 
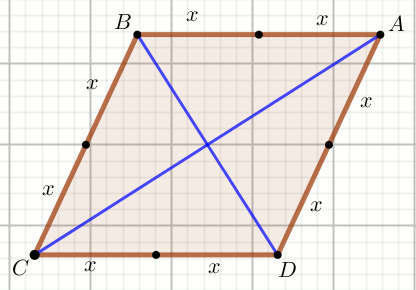
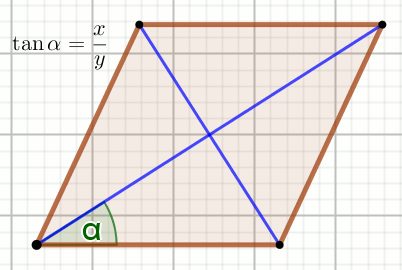
Podpunkt 29.1 (4 pkt)
 Czworokąt na rysunku jest rombem o polu powierzchni P:

Oblicz długość boku tego rombu.

Dane
x=3
y=4
P=24
Odpowiedź:
a= (wpisz liczbę całkowitą)
Zadanie 30.  4 pkt ⋅ Numer: pp-30119 ⋅ Poprawnie: 56/177 [31%] Rozwiąż 
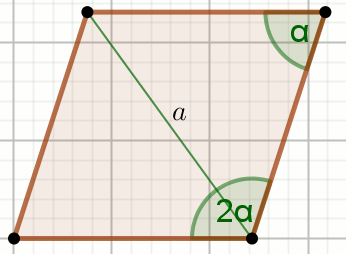
Podpunkt 30.1 (2 pkt)
 » Czworokąt na rysunku jest rombem:

Oblicz pole powierzchni tego rombu.

Dane
a=2
Odpowiedź:
P= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 30.2 (2 pkt)
 Oblicz wysokość tego rombu.
Odpowiedź:
h= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 31.  4 pkt ⋅ Numer: pp-30120 ⋅ Poprawnie: 9/63 [14%] Rozwiąż 
Podpunkt 31.1 (2 pkt)
 W równoległoboku ABCD o obwodzie 28 dane są stosunki: |DE|:|DF|=2:5 oraz |\sphericalangle BCD|:|\sphericalangle ABC|=1:2:

Oblicz |AB|.

Odpowiedź:
|AB|=
(wpisz dwie liczby całkowite)
Podpunkt 31.2 (2 pkt)
 Oblicz |AC|.
Odpowiedź:
|AC|= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 32.  4 pkt ⋅ Numer: pp-30121 ⋅ Poprawnie: 17/71 [23%] Rozwiąż 
Podpunkt 32.1 (4 pkt)
 « Okrąg przechodzi przez wierzchołek kąta ostrego i dwa wierzchołki kątów rozwartych rombu. Okrąg podzielił dłuższą przekątną tego rombu na odcinki o długościach 20 i 12.

Wyznacz pole powierzchni tego rombu.

Odpowiedź:
P= (wpisz liczbę całkowitą)
Zadanie 33.  4 pkt ⋅ Numer: pp-30122 ⋅ Poprawnie: 46/124 [37%] Rozwiąż 
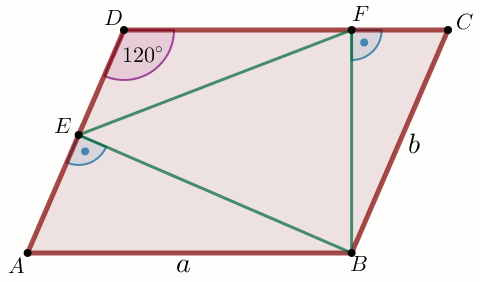
Podpunkt 33.1 (1 pkt)
 Czworokąt ABCD na rysunku jest równoległobokiem, w którym odcinki BE i BF są jego wysokościami, a kąt rozwarty ADC ma miarę 120^{\circ}.

Oblicz długośc odcinka BE.

Dane
|AB|=a=12
|AD|=b=10
Odpowiedź:
|BE|= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 33.2 (1 pkt)
 Oblicz obwód trójkąta BCF.
Odpowiedź:
L_{\triangle BCF}= + \cdot √
(wpisz trzy liczby całkowite)
Podpunkt 33.3 (2 pkt)
 Oblicz pole powierzchni trójkąta BFE.
Odpowiedź:
P_{\triangle BFE}= \cdot√
(wpisz trzy liczby całkowite)
Zadanie 34.  4 pkt ⋅ Numer: pp-30123 ⋅ Poprawnie: 17/68 [25%] Rozwiąż 
Podpunkt 34.1 (2 pkt)
 Czworokąt na rysunku jest równoległobokiem o polu powierzchni: 861, w którym |AB|=41 i |AD|=29:

Oblicz |BD|.

Odpowiedź:
|BD|= \cdot√
(wpisz dwie liczby całkowite)
Podpunkt 34.2 (2 pkt)
 Oblicz |AC|.
Odpowiedź:
|AC|= \cdot√
(wpisz dwie liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm