Pole powierzchni trapezu
Zadania dla liceum ogólnokształcącego - poziom podstawowy
pole powierzchni trapezu
wzory na pole trapezu
własności pola powierzchni
Zadanie 1. 1 pkt ⋅ Numer: pp-11488 ⋅ Poprawnie: 188/221 [85%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
Odcinek łączący środki ramion trapezu o wysokości
......... cm ma długość
\frac{13}{2} cm, a pole
powierzchni tego trapezu jest równe
26 cm
2 .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 2. 1 pkt ⋅ Numer: pp-11493 ⋅ Poprawnie: 80/105 [76%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
Odcinek łączący środki ramion trapezu ma długość
4 cm, a wysokość
tego trapezu ma długość
11 cm.
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 3. 1 pkt ⋅ Numer: pp-11490 ⋅ Poprawnie: 198/265 [74%]
Rozwiąż
Podpunkt 3.1 (1 pkt)
Wysokość trapezu równoramiennego o długości
\frac{19}{2} cm poprowadzona z wierzchołka kąta rozwartego
podzieliła dłuższą podstawę tego trapezu na odcinki mające długość
14 cm i
2 cm.
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 4. 2 pkt ⋅ Numer: pp-20471 ⋅ Poprawnie: 13/120 [10%]
Rozwiąż
Podpunkt 4.1 (2 pkt)
Cięciwy
AB i
CD okręgu o
promieniu
20 są równoległe i leżą po tej samej
stronie środka okręgu. Odległość dłuższej z cięciw od środka okręgu wynosi
x , a odległość między tymi cięciwami
wynosi
y .
Oblicz pole trapezu ABCD .
Dane
x=5 y=1
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 5. 2 pkt ⋅ Numer: pp-20472 ⋅ Poprawnie: 53/138 [38%]
Rozwiąż
Podpunkt 5.1 (2 pkt)
Wysokość trapezu równoramiennego wynosi
h , a sinus
kąta ostrego tego trapezu jest równy
\frac{p}{q} .
Stosunek długości podstaw tego trapezu jest równy
1:3 .
Oblicz pole tego trapezu.
Dane
h=60 p=60 q=109
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 6. 2 pkt ⋅ Numer: pp-20473 ⋅ Poprawnie: 18/70 [25%]
Rozwiąż
Podpunkt 6.1 (1 pkt)
» W trapezie o polu powierzchni równym
P przekątne
przecinają się w punkcie
S , który dzieli wysokość
tego trapezu równą
h w stosunku
x:y .
Oblicz długość krótszej podstawy tego trapezu.
Dane
h=14 x=3 y=11 P=98
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 7. 2 pkt ⋅ Numer: pp-20474 ⋅ Poprawnie: 67/270 [24%]
Rozwiąż
Podpunkt 7.1 (2 pkt)
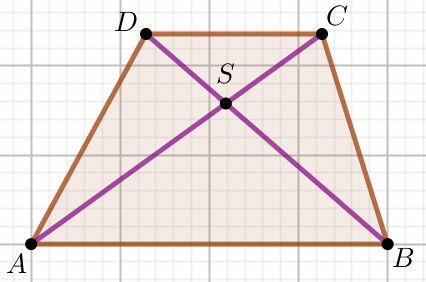
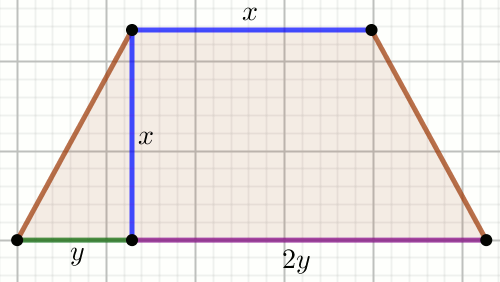
Czworokąt na rysunku jest trapezem:
Oblicz P_{ABCD} .
Dane
P_{DSC}=39 P_{ASD}=78
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 8. 2 pkt ⋅ Numer: pp-20786 ⋅ Poprawnie: 113/298 [37%]
Rozwiąż
Podpunkt 8.1 (2 pkt)
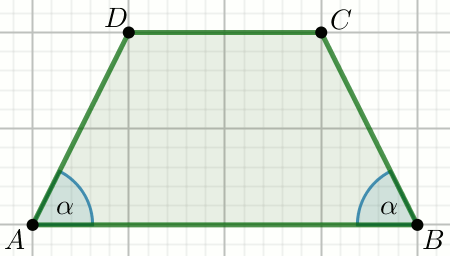
Czworokąt na rysunku jest trapezem prostokątnym:
Oblicz |DB| .
Dane
\alpha=30^{\circ} a=14
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 9. 2 pkt ⋅ Numer: pp-20476 ⋅ Poprawnie: 18/66 [27%]
Rozwiąż
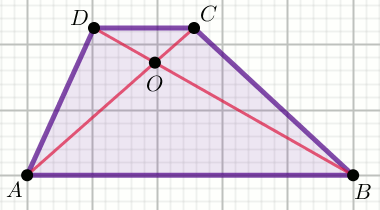
Podpunkt 9.1 (2 pkt)
Punkt przecięcia przekątnych trapezu
ABCD podzielił odcinek
AC na takie odcinki, że
|AO|:|OC|=7:2 :
Oblicz stosunek pól
\frac{P_{\triangle ABO}}{P_{\triangle DOC}} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 10. 2 pkt ⋅ Numer: pp-20477 ⋅ Poprawnie: 151/304 [49%]
Rozwiąż
Podpunkt 10.1 (2 pkt)
W trapezie prostokątnym kąt ostry ma miarę
\alpha ,
a podstawy tego trapezu mają długości
2 i
8 .
Wiedząc, że \tan\alpha=\frac{3}{2} oblicz pole powierzchni
tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 11. 2 pkt ⋅ Numer: pp-20475 ⋅ Poprawnie: 13/88 [14%]
Rozwiąż
Podpunkt 11.1 (2 pkt)
«« Przekątne trapezu
ABCD przecinają się w punkcie
O takim, że
|AO|=\frac{7}{9}|AC| .
Oblicz \frac{P_{\triangle DOC}}{P_{\triangle COB}} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 12. 2 pkt ⋅ Numer: pp-21059 ⋅ Poprawnie: 174/738 [23%]
Rozwiąż
Podpunkt 12.1 (2 pkt)
Dany jest trapez równoramienny
ABCD , w którym podstawa
CD
ma długość
9 , ramię
AD ma długość
2\sqrt{2} , a kąty
BAD oraz
ABC
mają miarę
45^{\circ} (zobacz rysunek).
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Zadanie 13. 2 pkt ⋅ Numer: pp-21129 ⋅ Poprawnie: 13/69 [18%]
Rozwiąż
Podpunkt 13.1 (2 pkt)
Dany jest trapez o podstawach długości
a oraz
b ,
i wysokości
h . Każdą z podstaw tego trapezu wydłużono o
5\% , a wysokość skrócono tak, że powstał nowy trapez o takim
samym polu.
Oblicz, o ile procent, z dokładnością do dwóch miejsc po przecinku, skrócono wysokość h trapezu.
Odpowiedź:
p\ [\%]=
(liczba zapisana dziesiętnie)
Zadanie 14. 4 pkt ⋅ Numer: pp-30124 ⋅ Poprawnie: 18/89 [20%]
Rozwiąż
Podpunkt 14.1 (2 pkt)
« Czworokąt na rysunku jest trapezem:
Oblicz |BC| .
Dane
a=24 c=32
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (1 pkt)
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.3 (1 pkt)
Oblicz
\frac{P_{\triangle ABP}}{P_{\triangle CDP}} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 15. 4 pkt ⋅ Numer: pp-30125 ⋅ Poprawnie: 6/89 [6%]
Rozwiąż
Podpunkt 15.1 (2 pkt)
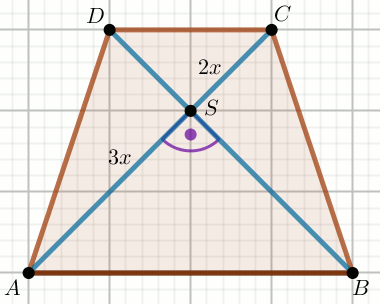
« W trapezie
ABCD o podstawach długości
|AB|=a i
|CD|=b przekątne
przecinają się w punkcie
S takim, że
P_{\triangle BCS}=p .
Oblicz P_{\triangle ABS} .
Dane
a=12 b=60 p=10
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.2 (2 pkt)
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 16. 4 pkt ⋅ Numer: pp-30126 ⋅ Poprawnie: 43/95 [45%]
Rozwiąż
Podpunkt 16.1 (2 pkt)
Czworokąt na rysunku jest trapezem równoramiennym:
Oblicz miarę stopniową kąta ostrego tego trapezu.
Dane
P=162
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (1 pkt)
Pole powierzchni tego trapezu jest równe
P .
Oblicz długość krótszej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.3 (1 pkt)
Oblicz długość dłuższej podstawy tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 17. 4 pkt ⋅ Numer: pp-30127 ⋅ Poprawnie: 8/63 [12%]
Rozwiąż
Podpunkt 17.1 (1 pkt)
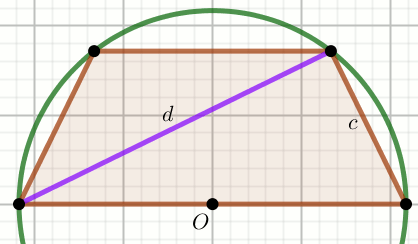
Czworokąt na rysunku jest trapezem, a punkt
O
środkiem okręgu:
Oblicz promień tego okręgu.
Dane
d=\frac{80}{3}=26.6666666666667 c=20
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.2 (1 pkt)
Oblicz długość wysokości tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.3 (2 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 18. 4 pkt ⋅ Numer: pp-30128 ⋅ Poprawnie: 44/121 [36%]
Rozwiąż
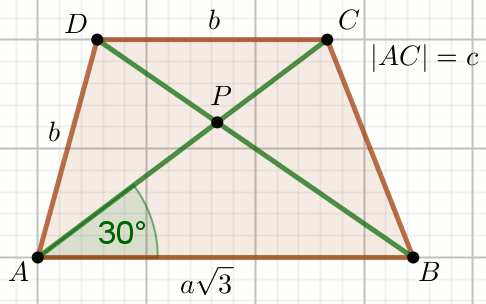
Podpunkt 18.1 (4 pkt)
« Oblicz pole powierzchni trapezu pokazanego na rysunku:
Dane
|AD|=|BC|=\sqrt{650}=25.49509756796392 |AS|:|SC|=3:2=1.50000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 19. 4 pkt ⋅ Numer: pp-30131 ⋅ Poprawnie: 23/84 [27%]
Rozwiąż
Podpunkt 19.1 (4 pkt)
» Przekątna trapezu równoramiennego o długości
18 ,
jest prostopadła do ramienia tego trapezu. Kąt ostry tego trapezu
ma miarę
60^{\circ} .
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 20. 4 pkt ⋅ Numer: pp-30130 ⋅ Poprawnie: 29/78 [37%]
Rozwiąż
Podpunkt 20.1 (4 pkt)
Czworokąt
ABCD jest trapezem, w którym
|AO|=5\cdot |CO| oraz
P_{\triangle BCO}=10 .
Oblicz pole trapezu ABCD .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat
Masz pytania? Napisz: k42195@poczta.fm