⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Kąt między prostymi
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
- kąt między dwoma prostymi
- kąt przecięcia się prostych
- równanie kierunkowe prostej
| Zadanie 1. 2 pkt ⋅ Numer: pr-20359 ⋅ Poprawnie: 30/61 [49%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Przekątna AC rombu ABCD,
w którym A=(x_a,y_a) i
D=(x_d,y_d), zawarta jest w prostej
ax+by+c=0.
Wyznacz B=(x_b,y_b)
Podaj x_b.
Dane
x_a=3
y_a=-\frac{3}{2}=-1.500000000000000
x_d=7
y_d=\frac{3}{2}=1.500000000000000
a=1
b=-3
c=-\frac{15}{2}=-7.500000000000000
y_a=-\frac{3}{2}=-1.500000000000000
x_d=7
y_d=\frac{3}{2}=1.500000000000000
a=1
b=-3
c=-\frac{15}{2}=-7.500000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 1.2 (1 pkt)
Podaj y_b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 2 pkt ⋅ Numer: pr-20363 ⋅ Poprawnie: 27/63 [42%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Punkt B=(x_b,y_b) jest symetryczny do punktu
A=(x_a,y_a) względem prostej o równaniu
ax+by+c=0
Podaj x_b.
Dane
x_a=-3
y_a=\frac{1}{2}=0.500000000000000
a=2
b=-1
c=-7.0000000000
y_a=\frac{1}{2}=0.500000000000000
a=2
b=-1
c=-7.0000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 2.2 (1 pkt)
Podaj y_b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pr-20364 ⋅ Poprawnie: 39/85 [45%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
» Proste y=a_1x+b_1 oraz
y=a_2x+b_2 przecinaja się pod kątem ostrym
\alpha.
Podaj \sin\alpha.
Dane
a_1=1
b_1=-17
a_2=2-\sqrt{3}=0.267949192431
b_2=3+5\sqrt{3}=11.6602540378443860
b_1=-17
a_2=2-\sqrt{3}=0.267949192431
b_2=3+5\sqrt{3}=11.6602540378443860
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 2 pkt ⋅ Numer: pr-20365 ⋅ Poprawnie: 16/24 [66%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Proste y=a_1x+b_1 oraz
y=a_2x+b_2 przecinają się pod kątem ostrym
\alpha.
Podaj \sin\alpha.
Dane
a_1=\frac{\sqrt{3}}{3}=0.5773502691896258
b_1=\frac{-9-5\sqrt{3}}{3}=-5.8867513459481288
a_2=-\frac{\sqrt{3}}{3}=-0.5773502691896258
b_2=\frac{5\sqrt{3}}{3}=2.8867513459481288
b_1=\frac{-9-5\sqrt{3}}{3}=-5.8867513459481288
a_2=-\frac{\sqrt{3}}{3}=-0.5773502691896258
b_2=\frac{5\sqrt{3}}{3}=2.8867513459481288
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 2 pkt ⋅ Numer: pr-20366 ⋅ Poprawnie: 21/50 [42%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Punkty A=(x_a,y_a) i
C=(x_c,y_c) są przeciwległymi wierzchołkami
prostokąta ABCD, zaś wierzchołek
D tego prostokąta należy do prostej
y+c=0.
Wyznacz B=(x_b,y_b).
Podaj najmniejsze możliwe x_b.
Dane
x_a=12
y_a=-\frac{2}{3}=-0.666666666666667
x_c=0
y_c=\frac{10}{3}=3.333333333333333
c=\frac{14}{3}=4.666666666666667
y_a=-\frac{2}{3}=-0.666666666666667
x_c=0
y_c=\frac{10}{3}=3.333333333333333
c=\frac{14}{3}=4.666666666666667
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (1 pkt)
Podaj największe możliwe x_b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pr-20367 ⋅ Poprawnie: 6/48 [12%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
» Prosta x+2y-\frac{17}{3}=0 zawiera przekątną
AC kwadratu ABCD o obwodzie
16\sqrt{10} i wierzchołku
B=\left(9,\frac{25}{3}\right).
Wyznacz A=(x_a,y_a) (odwrotnie do ruchu wskazówek zegara).
Wyznacz A=(x_a,y_a) (odwrotnie do ruchu wskazówek zegara).
Podaj x_a+y_a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Wyznacz D=(x_d,y_d)
(odwrotnie do ruchu wskazówek zegara).
Podaj x_d+y_d.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pr-20368 ⋅ Poprawnie: 6/16 [37%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
» Proste x+y-1=0 i
x-\sqrt{3}y=0 przecinają się pod kątem ostrym
\alpha.
Podaj \alpha.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20369 ⋅ Poprawnie: 4/12 [33%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Prosta x+(9-m^2)y-4m=0 przecina prostą o równaniu
3x+3y-4=0 pod kątem
\beta=45^{\circ}. Wyznacz
m.
Podaj najmniejsze możliwe m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Podaj największe możliwe m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 4 pkt ⋅ Numer: pr-20370 ⋅ Poprawnie: 2/5 [40%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« Odcinek o długości 4 zawarty jest w prostej
o równaniu 3x-4y-22=0. Symetralna tego odcinka
przecięła oś Oy w punkcie
A=(0,2). Wyznacz współrzedne końców tego odcinka.
Podaj sumę odciętej i rzędnej tego punktu, który ma obie współrzędne całkowite.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (1 pkt)
Podaj odciętą drugiego z punktów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.3 (1 pkt)
Podaj rzędną drugiego z punktów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 4 pkt ⋅ Numer: pr-20360 ⋅ Poprawnie: 5/12 [41%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
W rombie o boku długości 5 końcami przekątnej są
punkty A=(-9,5) i B=(-1,9).
Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Podaj sumę rzędnych dwóch pozostałych wierzchołków.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (2 pkt)
Podaj sumę odciętych dwóch pozostałych wierzchołków.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 4 pkt ⋅ Numer: pr-20361 ⋅ Poprawnie: 11/30 [36%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
«« W rombie o polu 300 punkt
S=(8, 2) jest punktem przecięcia przekątnych, a
punkt A=(7,-5) jednym z wierzchołków tego rombu.
Wyznacz pozostałe wierzchołki.
Punkty B=(x_B,y_B) i D=(x_D,y_D) są dwoma przeciwległymi wierzchołkami tego rombu (odwrotnie do ruchu wskazówek zegara).
Podaj min(x_B, x_D).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (2 pkt)
Podaj max(x_B, x_D).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. 4 pkt ⋅ Numer: pr-20362 ⋅ Poprawnie: 6/46 [13%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
«« Punkty A=(-3,-5) i B=(1,-7)
są kolejnymi wierzchołkami czworokąta ABCD
(odwrotnie do ruchu wskazówek zegara) wpisanego w okrąg, którego osią symetrii
jest prosta x-y-2=0.
Wyznacz C=(x_c,y_c) i D=(x_d,y_d).
Wyznacz C=(x_c,y_c) i D=(x_d,y_d).
Podaj x_c+y_c.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (2 pkt)
Podaj x_d+y_d.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. 4 pkt ⋅ Numer: pr-30267 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Przez punkt A=(x_a,y_a) przechodzą proste
y=a_1x+b_1 i y=a_2x+b_2,
które z prostą o równaniu 2x-y+c=0 tworzą kąt o
mierze 45^{\circ}.
Podaj min(a_1,a_2).
Dane
x_a=5
y_a=-2
c=-7
y_a=-2
c=-7
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (1 pkt)
Podaj max(a_1,a_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.3 (1 pkt)
Podaj min(b_1,b_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.4 (1 pkt)
Podaj max(b_1,b_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. 4 pkt ⋅ Numer: pr-30268 ⋅ Poprawnie: 0/2 [0%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
« Przez punkt A=(x_a,y_a) przechodzą proste
y=a_1x+b_1 i y=a_2x+b_2,
które z prostą o równaniu \sqrt{3}x-y+c=0 tworzą kąt
o mierze 60^{\circ}.
Podaj min(a_1,a_2).
Dane
x_a=5
y_a=-2
c=-5\sqrt{3}=-8.6602540378443865
y_a=-2
c=-5\sqrt{3}=-8.6602540378443865
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (1 pkt)
Podaj max(a_1,a_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.3 (1 pkt)
Podaj min(b_1,b_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.4 (1 pkt)
Podaj max(b_1,b_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. 4 pkt ⋅ Numer: pr-30269 ⋅ Poprawnie: 1/3 [33%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
» Przez punkt A=(x_a,y_a) przechodzą proste
y=a_1x+b_1 i y=a_2x+b_2,
które z prostą o równaniu x-y+c=0 tworzą kąt
o mierze 30^{\circ}.
Podaj \min(a_1,a_2).
Dane
x_a=6
y_a=-3
c=-6
y_a=-3
c=-6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.2 (1 pkt)
Podaj \max(a_1,a_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.3 (1 pkt)
Podaj \min(b_1,b_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.4 (1 pkt)
Podaj \max(b_1,b_2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 16. 4 pkt ⋅ Numer: pr-30270 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 16.1 (2 pkt)
« Punkty A=(-4,-2) i
C=(0,0) są wierzchołkami rombu o kącie
ostrym 60^{\circ} przy wierzchołku
B. Wyznacz B=(x_B,y_B) i
D=(x_D,y_D) (odwrotnie do wskazówek zegara).
Podaj x_D.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (2 pkt)
Podaj y_B.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. 4 pkt ⋅ Numer: pr-30271 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 17.1 (2 pkt)
Punkt P=(-2,2) jest środkiem symetrii rombu
ABCD, w którym
\overrightarrow{AC}=[12,6] i
\overrightarrow{AB}\parallel k:y=-\frac{1}{2}x-1.
Wyznacz B=(x_b,y_b) i
D=(x_d,y_d) .
Podaj x_b+y_b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 17.2 (2 pkt)
Podaj x_d+y_d.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 18. 4 pkt ⋅ Numer: pr-30272 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 18.1 (2 pkt)
» Czworokąt ABCD na rysunku jest równoległobokiem:
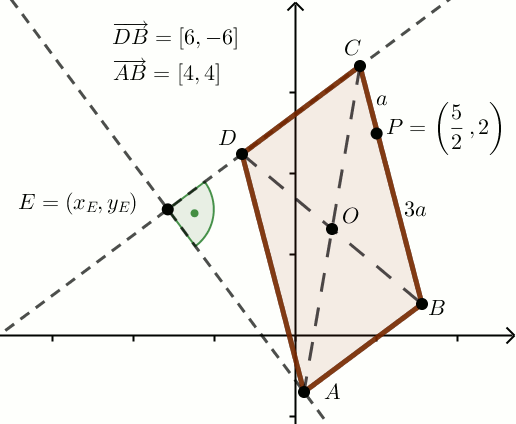
Podaj x_E.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 18.2 (2 pkt)
Podaj y_E.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 19. 4 pkt ⋅ Numer: pr-30273 ⋅ Poprawnie: 4/4 [100%] | Rozwiąż |
Podpunkt 19.1 (4 pkt)
Poprowadzono styczne do paraboli y=\frac{1}{4}x^2+3
przechodzące przez początek układu współrzędnych. Oblicz miarę stopniową
kąta ostrego między tymi stycznymi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)