Zadania różne z geometrii analitycznej
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- równania ogólne i kierunkowe prostych
- wielokąty w układziew współrzędnych
- kwadraty i prostokąty w układzie współrzędnych
- romby i równoległoboki w układzie współrzędnych
- trapezy w układzie współrzędnych
- czworokąty w układzie współrzędnych
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10226 |
Podpunkt 1.1 (1 pkt)
Równanie x^2+4x=y^2-4 opisuje na płaszczyźnie
Odpowiedzi:
| A. punkt | B. parabolę |
| C. dwie proste | D. okrąg |
| E. prostą | F. zbiór pusty |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10459 |
Podpunkt 2.1 (1 pkt)
Równanie x^2+4x=-4-y^2 opisuje na płaszczyźnie
Odpowiedzi:
| A. punkt | B. zbiór pusty |
| C. okrąg | D. prostą |
| E. parabolę | F. dwie proste |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-10227 |
Podpunkt 3.1 (1 pkt)
Równanie y^2-2x^2=0 opisuje na płaszczyźnie:
Odpowiedzi:
| A. dwie proste prostopadłe | B. punkt |
| C. dwie proste przecinające się pod kątem innym niż prosty | D. parabolę |
| E. prostą | F. okrąg |
| Zadanie 6. (6 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-31000 |
Podpunkt 6.1 (1 pkt)
W kartezjańskim układzie współrzędnych (x, y) prosta
l o równaniu x-y-4=0 przecina parabolę o
równaniu y=4x^2-15x+11 w punktach A oraz
B. Odcinek AB jest średnicą okręgu
\mathcal{O}. Punkt C leży na okręgu
\mathcal{O} nad prostąl, a kąt
BAC jest ostry i ma miarę \alpha taką,
że \tan\alpha=\frac{1}{3} (zobacz rysunek).
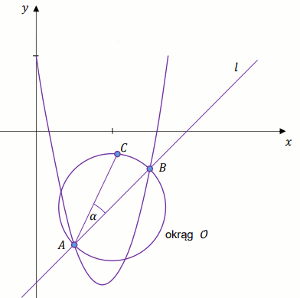
Wyznacz współrzędne punktów A=(x_A, y_A) i B=(x_B, y_B) przy czym x_A\lessdot x_B.
Podaj współrzędne punktu A.
Odpowiedzi:
| x_A | = | (dwie liczby całkowite) | |
| y_A | = | (dwie liczby całkowite) | |
Podpunkt 6.2 (1 pkt)
Podaj współrzędne punktu B.
Odpowiedzi:
| x_B | = | (dwie liczby całkowite) | |
| y_B | = | (dwie liczby całkowite) | |
Podpunkt 6.3 (2 pkt)
Wyznacz równanie prostej AC: y=ax+b.
Podaj współczynniki a i b.
Odpowiedzi:
| a | = | (dwie liczby całkowite) | |
| b | = | (dwie liczby całkowite) | |
Podpunkt 6.4 (1 pkt)
Wyznacz równanie prostej BC: y=mx+n.
Podaj współczynniki m i n.
Odpowiedzi:
| m | = | (dwie liczby całkowite) | |
| n | = | (dwie liczby całkowite) | |
Podpunkt 6.5 (1 pkt)
Wyznacz współrzędne punktu C=(x_C, y_C).
Odpowiedzi:
| x_C | = | (dwie liczby całkowite) | |
| y_C | = | (dwie liczby całkowite) | |
| Zadanie 7. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-31884 |
Podpunkt 7.1 (1 pkt)
W okrąg o równaniu (x+4)^2+(y+4)^2=25
wpisano trójkąt ABC. Bok AB tego
trójkąta jest zawarty w prostej o równaniu 4x-3y+4=0,
przy czym rzędna punktu A jest mniejsza od rzędnej punktu B.
Wysokość CD tego trójkąta dzieli bok AB
tak, że |AD|=\frac{1}{4}|DB|.
Wyznacz współrzędne punktu D=(x_D, y_D).
Odpowiedzi:
| x_D | = | (dwie liczby całkowite) | |
| y_D | = | (dwie liczby całkowite) | |
Podpunkt 7.2 (1 pkt)
Wyznacz współrzędne punktu C=(x_C, y_C).
Podaj najmniejszą i największą możliwą wartość odciętej x_C.
Odpowiedzi:
| MIN_{x_C} | = | (dwie liczby całkowite) | |
| MAX_{x_C} | = | (dwie liczby całkowite) | |
Podpunkt 7.3 (1 pkt)
Oblicz wysokość trójkąta ABC.
Odpowiedź:
| |CD|= | |
Podpunkt 7.4 (1 pkt)
Oblicz pole trójkąta ABC.
Odpowiedź:
| P_{ABC}= | |
Liczba wyświetlonych zadań: 5
Liczba pozostałych zadań dostępnych dla zarejestrowanych nauczycieli: 4