⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Przekształcenia wykresu funkcji wykładniczej
Zadania dla liceum ogólnokształcącego - poziom podstawowy
- wykres funkcji wykładniczej
- własności funkcji wykładniczej
- przekształcenia wykresu
- przesunięcie wykresu o wektor
- symetrie wykresu
| Zadanie 1. 1 pkt ⋅ Numer: pp-11189 ⋅ Poprawnie: 97/141 [68%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Zbiór wartości funkcji f(x)=2^x+2\sqrt{5}
zawiera liczbę:
Odpowiedzi:
| A. -22 | B. \frac{\sqrt{20}}{6} |
| C. \sqrt{20}+1 | D. \sqrt{20}-5 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11214 ⋅ Poprawnie: 235/398 [59%] | Rozwiąż |
Podpunkt 2.1 (0.2 pkt)
Zbiór wartości funkcji f(x)=8^{-x}-2 ma postać:
Odpowiedzi:
| A. (-\infty, p)\cup(q, +\infty) | B. (-\infty, p) |
| C. (p,+\infty) | D. \langle p, q\rangle |
| E. \langle p, +\infty) | F. (-\infty, p\rangle |
Podpunkt 2.2 (0.8 pkt)
Zapisz ten zbiór w postaci sumy przedziałów.
Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11192 ⋅ Poprawnie: 47/88 [53%] | Rozwiąż |
Podpunkt 3.1 (0.2 pkt)
» Dana jest funkcja g(x)=-3^{3-x}-7.
Zbiór ZW_g ma postać:
Odpowiedzi:
| A. (-\infty, p)\cup(q, +\infty) | B. \langle p, q\rangle |
| C. (p, q) | D. \langle p, +\infty) |
| E. (-\infty,p) | F. (-\infty, p\rangle |
Podpunkt 3.2 (0.8 pkt)
Zapisz ten zbiór w postaci sumy przedziałów.
Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
| min= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11193 ⋅ Poprawnie: 71/124 [57%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Wykres funkcji g jest symetryczny do wykresu
funkcji f(x)=9^{-x} względem pewnej prostej.
Zatem g(x) jest równe:
Odpowiedzi:
| A. -9^{-x} | B. -9^{x} |
| C. \left(\frac{1}{7}\right)^{x} | D. 9^{-x}-8 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11198 ⋅ Poprawnie: 241/398 [60%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Funkcją malejącą jest funkcja określona wzorem:
Odpowiedzi:
| A. h(x)=8^{1-x} | B. h(x)=\left(\frac{1}{8}\right)^{8-x} |
| C. h(x)=-8^{-x} | D. h(x)=\left(\frac{1}{8}\right)^{-x} |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11204 ⋅ Poprawnie: 208/479 [43%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Przesuwając wykres funkcji wykładniczej
f(x)=\left(\frac{1}{a}\right)^x o dwie jednostki
w prawo otrzymamy wykres funkcji g określonej wzorem:
Odpowiedzi:
| A. g(x)=\left(\frac{1}{11}\right)^{x}-2 | B. g(x)=121\cdot\left(\frac{1}{11}\right)^x |
| C. g(x)=11\cdot\left(\frac{1}{11}\right)^{x+1} | D. g(x)=\left(\frac{1}{11}\right)^{x}+2 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11206 ⋅ Poprawnie: 131/229 [57%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
» Wykres funkcji f(x)=\frac{1}{625}\cdot 5^x otrzymamy
przesuwając wykres funkcji g(x)=5^x o:
Odpowiedzi:
| A. cztery jednostki w prawo | B. cztery jednostki w lewo |
| C. cztery jednostki w dół | D. dwie jednostki w górę |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11207 ⋅ Poprawnie: 133/240 [55%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Dana jest funkcja f(x)=\left(\frac{1}{13}\right)^x.
Funkcja g(x)=f(x+6)-4:
Odpowiedzi:
| A. ma jedno miejsce zerowe | B. ma więcej niż dwa miejsca zerowe |
| C. nie ma miejsc zerowych | D. ma dwa miejsca zerowe |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11212 ⋅ Poprawnie: 119/182 [65%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Dana jest funkcja f(x)=7^x+1.
Oblicz wartość funkcji określonej wzorem g(x)=f(x-2) dla argumentu x=7.
Odpowiedź:
g(7)=
(wpisz liczbę całkowitą)
| Zadanie 10. 1 pkt ⋅ Numer: pp-11213 ⋅ Poprawnie: 491/627 [78%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« Wykres funkcji f(x)=2^{x-3} przedstawia rysunek:
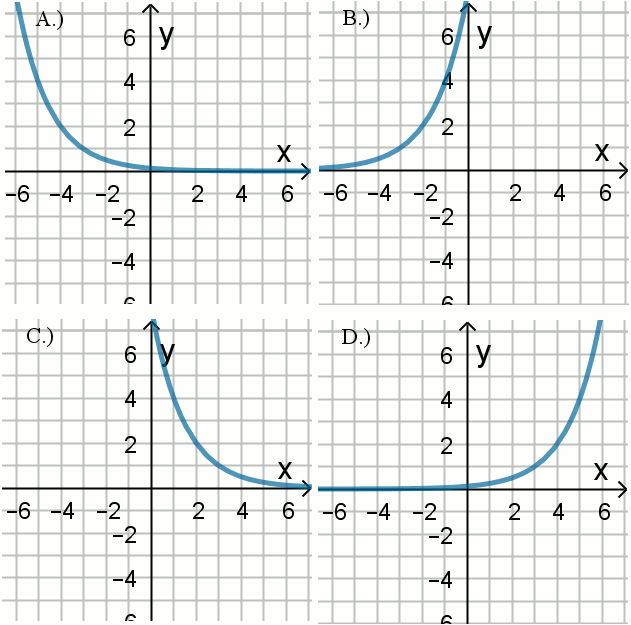
Odpowiedzi:
| A. D | B. C |
| C. A | D. B |
| Zadanie 11. 4 pkt ⋅ Numer: pp-30183 ⋅ Poprawnie: 28/156 [17%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
« Asymptotą poziomą wykresu funkcji g(x)=3^x+m jest
prosta y=a, a funkcja f
określona jest następująco: f(x)=g(-x).
Wyznacz m.
Dane
a=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (2 pkt)
Oblicz
f\left(\frac{1}{2}\right)-f\left(-\frac{1}{2}\right)
.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)