Własności funkcji logarytmicznej. Wykres funkcji logarytmicznej
Zadania dla liceum ogólnokształcącego - poziom rozszerzony
wykres funkcji logarytmicznej
własności funkcji logarytmicznej
monotoniczność funkcji logarytmicznej
Zadanie 1. 1 pkt ⋅ Numer: pr-10153 ⋅ Poprawnie: 0/1 [0%]
Rozwiąż
Podpunkt 1.1 (1 pkt)
Wyznacz dziedzinę funkcji określonej wzorem
f(x)=\log_{x}{(ax-1)} .
Rozwiązanie zapisz w postaci sumy przedziałów.
Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Dane
a=8
Odpowiedzi:
Zadanie 2. 1 pkt ⋅ Numer: pr-10156 ⋅ Poprawnie: 16/16 [100%]
Rozwiąż
Podpunkt 2.1 (1 pkt)
Oceń, które z podanych punktów należą do wykresu funkcji określonej wzorem
f(x)=\log_{a}{x} :
Dane
a=6
Odpowiedzi:
T/N : (1,0)
T/N : \left(\frac{1}{36}, -2\right)
Zadanie 3. 1 pkt ⋅ Numer: pr-10159 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 3.1 (1 pkt)
Ile liczb całkowitych należy do dziedziny funkcji określonej wzorem
g(x)=\log_{15}{(225-x^2)} ?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 4. 2 pkt ⋅ Numer: pr-20294 ⋅ Poprawnie: 11/15 [73%]
Rozwiąż
Podpunkt 4.1 (1 pkt)
Wyznacz wartości parametrów
p i
q wiedząc, że dziedziną funkcji
f(x)=\log_{\frac{1}{2}}{(x-p)}+q jest przedział
(-1,+\infty) i do wykresu należy punkt
P=\left(31,-3\right) .
Podaj p .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.2 (1 pkt)
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 5. 2 pkt ⋅ Numer: pr-20297 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 5.1 (1 pkt)
Wyznacz dziedzinę funkcji
f(x)=\log_{x+1}{5}-\log_{x+3}{(-x+3)} .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z tych końców tych
przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (1 pkt)
Podaj ten z końców tych przedziałów, który nie jest ani najmniejszy, ani też
największy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 6. 3 pkt ⋅ Numer: pr-20298 ⋅ Poprawnie: 0/2 [0%]
Rozwiąż
Podpunkt 6.1 (1 pkt)
Wyznacz dziedzinę funkcji
f(x)=\log_{x^2-1}{(x^4x^3-12x^2-16x)} .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z tych końców przedziałów,
który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Podaj największy z tych końców przedziałów,
który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.3 (1 pkt)
Podaj sumę tych ujemnych końców przedziałów,
które są liczbami (każdy ujemny koniec sumujemy tylko raz).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 7. 3 pkt ⋅ Numer: pr-20299 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 7.1 (1 pkt)
» Wyznacz dziedzinę funkcji
f(x)=\log{\frac{2x+13}{x+\frac{17}{2}}}+\log_{0,5}{(-12-2x)} .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z tych końców
przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.2 (1 pkt)
Podaj największy z tych końców przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.3 (1 pkt)
Podaj ten z końców przedziałów, który jest liczbą i nie jest ani najmniejszy, ani też największy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 8. 2 pkt ⋅ Numer: pr-20300 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 8.1 (1 pkt)
Wyznacz dziedzinę funkcji
f(x)=\log_{\frac{x+3}{x+7}}{\left(x^3+11x^2+32x+28\right)}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z tych wszystkich końców
tych przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Podaj największy z tych wszystkich końców
tych przedziałów, który jest liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 9. 2 pkt ⋅ Numer: pr-20301 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 9.1 (1 pkt)
» Wyznacz dziedzinę funkcji
f(x)=\log_{\frac{x}{x+2}}{(x^3-3x^2+4)}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj długość najkrótszego
z tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (1 pkt)
Podaj sumę wszystkich końców tych przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 10. 2 pkt ⋅ Numer: pr-20302 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 10.1 (2 pkt)
» Wyznacz dziedzinę funkcji
f(x)=\log_{x+2}{\frac{x^2-7x}{x^2+2x}}
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę tych wszystkich
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 11. 2 pkt ⋅ Numer: pr-20303 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 11.1 (2 pkt)
» Dla jakich wartości parametru
m dziedziną funkcji
g(x)=\sqrt{
\log{
\left(x^2+4x+3m\right)
}
}
jest zbiór
\mathbb{R} ?
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę tych wszystkich
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 12. 2 pkt ⋅ Numer: pr-20304 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 12.1 (1 pkt)
Dana jest funkcja
f(x)=\log_{\frac{\sqrt{2}}{2}}{\left(-x^2+12x-20\right)}
.
Wyznacz
D_f .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę tych wszystkich
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (1 pkt)
Wyznacz f_{min} .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 13. 2 pkt ⋅ Numer: pr-20295 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 13.1 (1 pkt)
«« Dana jest funkcja
h(x)=\log_{\frac{-x}{x+5}}{\frac{x^2+5x+4}{x+1}}
.
Wyznacz
D_h .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę tych wszystkich
końców przedziałów, które są liczbami całkowitymi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 13.2 (1 pkt)
Podaj sumę tych wszystkich końców przedziałów, które nie są liczbami
całkowitymi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 14. 2 pkt ⋅ Numer: pr-20296 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 14.1 (1 pkt)
Dla jakich wartości parametru
m\in\mathbb{R}
dziedziną funkcji
g(x)=\log{
\left(
\frac{m}{2x^2+2mx+\frac{m}{2}+3}
\right)
}
.
jest zbiór
\mathbb{R} .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę tych wszystkich
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (1 pkt)
Podaj długość rozwiązania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 15. 2 pkt ⋅ Numer: pr-20313 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 15.1 (1 pkt)
« Dana jest funkcja
g(x)=x^2+\log_{1024}{x}\cdot |2\log_{x}{32}|-4
.
Wyznacz
ZW_g .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę tych wszystkich
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 15.2 (1 pkt)
Podaj długość najkrótszego z tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 16. 2 pkt ⋅ Numer: pr-20315 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 16.1 (1 pkt)
Rozwiąż graficznie nierówność
\log_{7}{\frac{7\sqrt{7}}{x}} \geqslant \log_{5}{(\sqrt{5}x)}+1
w liczbach dodatnich.
Podaj największą z liczb spełniających tę nierówność.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 16.2 (1 pkt)
Podaj długość rozwiązania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 17. 2 pkt ⋅ Numer: pr-20499 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 17.1 (2 pkt)
Oblicz ilość liczb całkowitych należących do dziedziny funkcji
f(x)=\log{\left(1000-\frac{3}{8}x^2\right)} .
Zakoduj cyfry: setek, dziesiątek i jedności rozwinięcia dziesiętnego
otrzymanego wyniku.
Odpowiedź:
Wpisz odpowiedź:
(wpisz odpowiedź tekstową)
Zadanie 18. 4 pkt ⋅ Numer: pr-30207 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 18.1 (4 pkt)
Wyznacz wszystkie wartości parametru
m , dla których
dziedziną funkcji
f(x)=\log{[(m^2+5m)x^2+mx+1]}
jest zbiór wszystkich liczb rzeczywistych.
Podaj najmniejszą możliwą wartość m , która
nie spełnia warunków zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 19. 4 pkt ⋅ Numer: pr-30208 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 19.1 (2 pkt)
Dla jakich wartości parametru
m dziedziną funkcji
f(x)=\log_{0,5}{|mx^2+2\sqrt{2}x+m+1|} jest zbiór
\mathbb{R} ?
Ile liczb całkowitych z przedziału
\langle -100,100\rangle spełnia ten warunek?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 19.2 (2 pkt)
Ile liczb całkowitych m nie spełnia tego warunku?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 20. 4 pkt ⋅ Numer: pr-30209 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 20.1 (2 pkt)
» Wyznacz te wartości parametru
m , dla których
dziedziną funkcji
g(x)=\log{\left( \frac{1}{2}x^2+(m+1)x-m-1 \right)}
jest zbiór liczb rzeczywistych.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z tych
wszystkich końców tych przedziałów, który jeszt liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (2 pkt)
Podaj największy z tych wszystkich końców tych przedziałów, który jeszt liczbą.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 21. 4 pkt ⋅ Numer: pr-30210 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 21.1 (2 pkt)
Wyznacz dziedzinę funkcji
f(x)=\log_{(2x+6)}{\frac{x-3}{x+2}} .
Podaj liczbę ujemną z przedziału (-3,-2) , która
nie należy do dziedziny.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 21.2 (2 pkt)
Podaj największą liczbę dodatnią, która nie należy do dziedziny.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 22. 4 pkt ⋅ Numer: pr-30211 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 22.1 (2 pkt)
Dana jest funkcja
g(x)=\log_{\frac{\sqrt{2}}{2}}{(8x-x^2)} .
Wyznacz dziedzinę tej funkcji.
Podaj długość wyznaczonego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 22.2 (2 pkt)
Podaj najmniejszą wartość funkcji g .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 23. 4 pkt ⋅ Numer: pr-30212 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 23.1 (2 pkt)
Dla jakich wartości parametru
m dziedziną funkcji
f(x)=\log{(mx^2-4x+m+3)} jest zbiór
\mathbb{R} ?
Ile liczb całkowitych z przedziału
\langle -100,100\rangle spełnia ten warunek?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 23.2 (2 pkt)
Podaj najmniejszą dodatnią liczbę całkowitą m ,
która spełnia ten warunek.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 24. 4 pkt ⋅ Numer: pr-30213 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 24.1 (2 pkt)
» Dana jest funkcja
f(x)=\log_{0,4}{\frac{x+3}{6-x}} .
Wyznacz D_f . Zapisz rozwiązanie w postaci sumy
przedziałów. Podaj łączną długość tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 24.2 (2 pkt)
Jakie jest miejsce zerowe tej funkcji?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 25. 4 pkt ⋅ Numer: pr-30214 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 25.1 (2 pkt)
» Dana jest funkcja
g(x)=10x^3-\frac{1}{2}x .
Rozwiąż nierówność
g(x) > 0 .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę kwadratów tych
wszystkich końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 25.2 (1 pkt)
Dana jest funkcja
f(x)=\log_{3}{(-x)}+\log_{3}{\left(-\frac{g(x)}{x}\right)}
.
Wyznacz
D_f .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj największy z końców
tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 25.3 (1 pkt)
Podaj najmniejszy z końców tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 26. 4 pkt ⋅ Numer: pr-30223 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 26.1 (2 pkt)
Dana jest funkcja
f(x)=\log_{0,4}{\frac{2x-a+3}{a-2x+6}} .
Wyznacz dziedzinę tej funkcji.
Rozwiązanie zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Dane
a=8
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 26.2 (2 pkt)
Podaj prawy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 27. 4 pkt ⋅ Numer: pr-30217 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 27.1 (2 pkt)
Dla jakich wartości parametru
m funkcja
g(x)=\log_{\frac{m+1}{m}}{x} jest malejąca?
Podaj prawy koniec wyznaczonego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 27.2 (2 pkt)
Ile liczb całkowitych z przedziału
\langle -10,10\rangle spełnia warunki zadania?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 28. 4 pkt ⋅ Numer: pr-30218 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 28.1 (2 pkt)
Naszkicuj wykres funkcji
f(x)=|1-\log_{2}{(x+2)}| .
Na podstawie wykresu ustal dla jakich wartości parametru
m równanie
f(x)=m ma
dwa różne rozwiązania różnych znaków.
Zapisz rozwiązanie w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 28.2 (2 pkt)
Ile liczb całkowitych m z przedziału
\langle -20,20\rangle spełnia warunki zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 29. 4 pkt ⋅ Numer: pr-30219 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 29.1 (2 pkt)
Naszkicuj wykres funkcji
f(x)=|\log_{3}{(x+1)}+2| .
Na podstawie wykresu ustal dla jakich wartości parametru
m równanie
f(x)=m ma
dwa różne rozwiązania różnych znaków.
Zapisz rozwiązanie w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 29.2 (2 pkt)
Ile liczb całkowitych m z przedziału
\langle -20,20\rangle spełnia warunki zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 30. 4 pkt ⋅ Numer: pr-30220 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 30.1 (2 pkt)
Naszkicuj wykres funkcji
f(x)=1-|\log_{2}{(x+4)}| .
Na podstawie wykresu ustal dla jakich wartości parametru
m równanie
f(x)=m ma
dwa różne rozwiązania różnych znaków.
Zapisz rozwiązanie w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 30.2 (2 pkt)
Ile liczb całkowitych m z przedziału
\langle -20,20\rangle spełnia warunki zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 31. 4 pkt ⋅ Numer: pr-30221 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 31.1 (2 pkt)
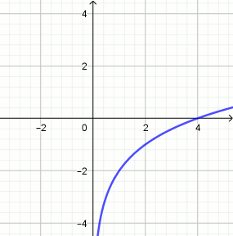
» Na rysunku pokazano wykres funkcji
f(x)=a+\log_{p}{x} .
Wyznacz a i p .
Podaj a-p .
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 31.2 (2 pkt)
Naszkicuj wykres funkcji
g(x)=|f(x+2)| .
Na podstawie wykresu ustal rozwiązanie nierówności
g(x) > 1 .
Ile liczb całkowitych z przedziału
\langle -10,10\rangle spełnia tę nierówność?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Zadanie 32. 4 pkt ⋅ Numer: pr-30222 ⋅ Poprawnie: 0/0
Rozwiąż
Podpunkt 32.1 (2 pkt)
Naszkicuj wykres funkcji
f(x)=\log_{2}{\left(-x^3-2x^2+4x+8\right)}-
\log_{2}{\left(-\frac{1}{2}x^2+2\right)}
.
Odczytaj z wykresu zbiór
ZW_f .
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich tych
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 32.2 (2 pkt)
Dla jakich wartości parametru
m prosta
x=m przecina wykres funkcji
f ?
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj sumę wszystkich tych
końców przedziałów, które są liczbami.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat
Masz pytania? Napisz: k42195@poczta.fm