Matury CKE ☆ Matma z CKE ☆ Sprawdziany ☆ Zadania z lekcji ☆ Zbiór zadań ☆ Wyniki uczniów ☆ Pomoc

Zaloguj mnie...

Załóż konto...

Ostrosłupy

Zadania dla klasy trzeciej liceum ogólnokształcącego - poziom rozszerzony

 

Zadanie 1.  1 pkt ⋅ Numer: pr-10249 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 1.1 (1 pkt)
Wierzchołkami wielościanu są środki wszystkich krawędzi czworościanu o objętości V. Objętość tego wielościanu wynosi:
Odpowiedzi:
A. \frac{1}{4}V B. \frac{2}{3}V
C. \frac{1}{2}V D. \frac{1}{8}V
E. \frac{1}{3}V F. \frac{1}{6}V
Zadanie 2.  3 pkt ⋅ Numer: pr-20803 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 2.1 (3 pkt)
 » Ostrosłup o podstawie ABC na rysunku jest prawidłowy:

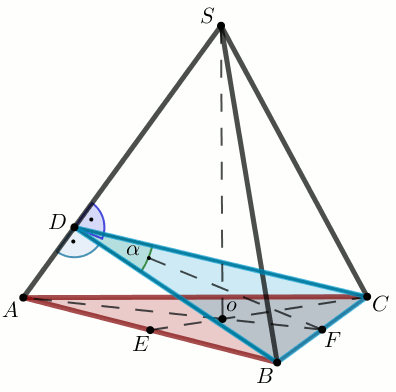
Oblicz tangens kąta pomiędzy dwoma sąsiednimi ścianami bocznymi tego ostrosłupa.

Dane
|AB|=12
|AS|=7\sqrt{6}=17.14642819948225
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 3.  4 pkt ⋅ Numer: pr-30344 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 3.1 (2 pkt)
» W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 6, a kąt między krawędzią boczną a podstawą jest równy kątowi płaskiemu przy wierzchołku.

Oblicz długość krawędzi bocznej tego ostrosłupa.

Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Podpunkt 3.2 (2 pkt)
Oblicz objętość tego ostrosłupa.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 4.  4 pkt ⋅ Numer: pr-30382 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 4.1 (2 pkt)
 » W ostrosłupie trójkątnym prawidłowym stosunek długości krawędzi bocznej do długości krawędzi podstawy jest równy k.

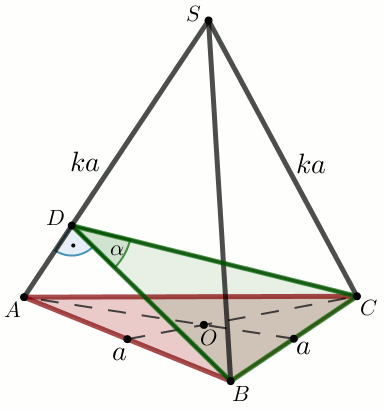
Oblicz |DS|:|DA|.

Dane
k=\frac{13}{10}=1.30000000000000
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Podpunkt 4.2 (2 pkt)
 Oblicz sinus kąta \alpha pod jakim przecinają się ściany boczne tego ostrosłupa.
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 5.  4 pkt ⋅ Numer: pr-30383 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 5.1 (4 pkt)
 W ostrosłupie trójkątnym prawidłowym stosunek cosinusa kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny jego podstawy, do cosinusa kąta płaskiego przy wierzchołku tego ostrosłupa, jest równy k.

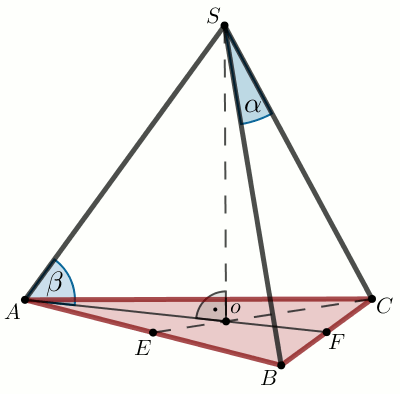
Oblicz \cos\alpha.

Dane
\frac{\cos\beta}{\cos\alpha}=k=3
Odpowiedź:
Wpisz odpowiedź:  (liczba zapisana dziesiętnie)
Zadanie 6.  6 pkt ⋅ Numer: pr-31002 ⋅ Poprawnie: 0/0 Rozwiąż 
Podpunkt 6.1 (1 pkt)
 Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma wysokości H ostrosłupa oraz promienia R okręgu opisanego na podstawie tego ostrosłupa jest równa 28.

Objętość V takiego ostrosłupa można zapisać w postaci V(R)=a\cdot R^2\cdot (b-R).
Podaj liczbę a.

Odpowiedź:
a= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 6.2 (1 pkt)
 Podaj liczbę b.
Odpowiedź:
b=
(wpisz dwie liczby całkowite)
Podpunkt 6.3 (1 pkt)
 Oblicz pochodną funkcji V.

Podaj wartość tej pochodnej w R=1.

Odpowiedź:
V'(1)= \cdot√
(wpisz trzy liczby całkowite)
Podpunkt 6.4 (1 pkt)
 Przy jakiej długości promienia R objętość rozważanego ostrosłupa jest największa?
Odpowiedź:
R=
(wpisz dwie liczby całkowite)
Podpunkt 6.5 (2 pkt)
 Ile jest równa ta maksymalna objętość ostrosłupa?
Odpowiedź:
V_{max}(R)= \cdot√
(wpisz trzy liczby całkowite)

☆ ⇒ [ Matma z CKE ] - zadania z matur z ostatnich lat

Masz pytania? Napisz: k42195@poczta.fm