⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd arkusza : lo2@cke-2021-03-pp
| Zadanie 1. 1 pkt ⋅ Numer: pp-12024 ⋅ Poprawnie: 114/141 [80%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Liczba (\sqrt{35}-\sqrt{5})^2-7\sqrt{7} jest równa:
Odpowiedzi:
| A. 40-24\sqrt{7} | B. 40-17\sqrt{7} |
| C. 40-10\sqrt{7} | D. 40-24\sqrt{35} |
| E. 40-24\sqrt{7} | F. 40-17\sqrt{5} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-12025 ⋅ Poprawnie: 104/125 [83%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Liczba 3\log_{5}{4}-2\log_{5}{\frac{1}{2}} jest równa:
Odpowiedzi:
| A. -\log_{5}{2^{8}} | B. 8\log_{5}{2} |
| C. -\log_{5}{2^{6}} | D. 5\log_{5}{2} |
| E. 6\log_{5}{2^{2}} | F. 6\log_{5}{2} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-12026 ⋅ Poprawnie: 74/83 [89%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Medyczna maseczka ochronna wielokrotnego użytku z wymiennymi filtrami wskutek podwyżki
zdrożała o 30\% i kosztuje obecnie
65.65 zł.
Cena maseczki w złotych przed podwyżką była równa:
Odpowiedzi:
| A. 50.50 | B. 53.54 |
| C. 50.11 | D. 49.49 |
| E. 44.49 | F. 46.20 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-12027 ⋅ Poprawnie: 111/136 [81%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Liczba \left(\sqrt[3]{b}\cdot\sqrt[2]{b}\right)^{\frac{1}{5}} jest równa:
Odpowiedzi:
| A. b^{\frac{1}{4}} | B. b^{\frac{1}{6}} |
| C. b^{\frac{1}{3}} | D. b^{\frac{1}{9}} |
| E. b^{\frac{1}{12}} | F. b^{\frac{1}{2}} |
| Zadanie 5. 1 pkt ⋅ Numer: pp-12028 ⋅ Poprawnie: 35/46 [76%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Para liczb x=1, y=-3 spełnia układ równań
\begin{cases}x-y=(a-7)^2\\(-6+a)x-3y=-4(a-7)\end{cases}.
Wtedy a jest równe:
Odpowiedzi:
| A. \frac{5}{2} | B. 7-\sqrt{2}} |
| C. 7+\sqrt{2}} | D. 5 |
| E. -5 | F. \frac{11}{2} |
| Zadanie 6. 1 pkt ⋅ Numer: pp-12029 ⋅ Poprawnie: 10/12 [83%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Iloczyn wszystkich rozwiązań równania 2(x-7)(x^2-25)=0 jest równy:
Odpowiedzi:
| A. 7 | B. -175 |
| C. 175 | D. -25 |
| E. 25 | F. -7 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-12030 ⋅ Poprawnie: 9/11 [81%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Zbiorem rozwiązań nierówności \frac{\frac{61}{8}-5x}{2}\lessdot 3\left(\frac{9}{16}-\frac{1}{2}x\right)+7x+\frac{49}{8} jest:
Odpowiedzi:
| A. \left(-\infty,\frac{5}{4}\right) | B. \left(-\infty,\frac{3}{2}\right) |
| C. \left(-\infty,\frac{11}{8}\right) | D. \left(-\frac{3}{8},+\infty\right) |
| E. \left(-\frac{1}{4},+\infty\right) | F. \left(-\frac{1}{2},+\infty\right) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-12031 ⋅ Poprawnie: 18/25 [72%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Funkcja liniowa f(x)=(a-7)x+3 osiąga wartość najmniejszą
równą 3.
Wtedy a jest równe:
Odpowiedzi:
| A. 1 | B. 11 |
| C. 7 | D. 10 |
| E. 2 | F. 5 |
| Zadanie 9. 1 pkt ⋅ Numer: pp-12032 ⋅ Poprawnie: 59/130 [45%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
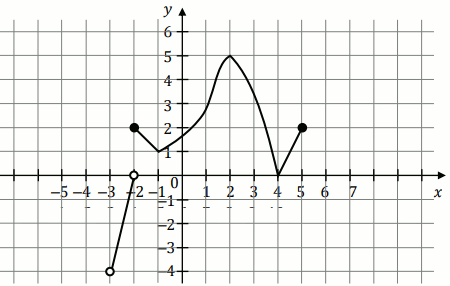
Na wykresie przedstawiono wykres funkcji f:
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja f jest rosnąca w przedziale (-4,-2] | T/N : zbiorem wartości funkcji f jest przedział (-4, 5\rangle |
| Zadanie 10. 1 pkt ⋅ Numer: pp-12033 ⋅ Poprawnie: 102/130 [78%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Funkcja f jest określona wzorem
f(x)=\frac{2x+2}{3x^2+3} dla każdej
liczby rzeczywistej x.
Wartość funkcji f dla argumentu 1 jest równa:
Odpowiedzi:
| A. \frac{2}{9} | B. \frac{5}{6} |
| C. \frac{1}{3} | D. 1 |
| E. \frac{8}{15} | F. \frac{2}{3} |
| Zadanie 11. 1 pkt ⋅ Numer: pp-12034 ⋅ Poprawnie: 39/49 [79%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Ciąg (x,y,z) jest geometryczny. Iloczyn wszystkich
wyrazów tego ciągu jest równy -125.
Wynika z tego, że y jest równe:
Odpowiedzi:
| A. -\frac{5}{2} | B. \frac{5}{2} |
| C. -5 | D. -10 |
| E. 5 | F. 10 |
| Zadanie 12. 1 pkt ⋅ Numer: pp-12035 ⋅ Poprawnie: 90/112 [80%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Ciąg (a_n), określony dla każdej liczby naturalnej
n > 1, jest arytmetyczny. Różnica tego ciągu jest
równa -5, a pierwszy wyraz tego ciągu jest równy
-5.
Wtedy iloraz \frac{a_4}{a_2} jest równy:
Odpowiedzi:
| A. \frac{4}{3} | B. 8 |
| C. 6 | D. 1 |
| E. 2 | F. 3 |
| Zadanie 13. 1 pkt ⋅ Numer: pp-12036 ⋅ Poprawnie: 12/14 [85%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
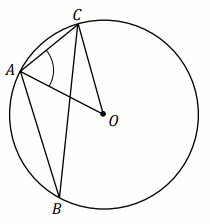
Trójkąt ABC jest wpisany w okrąg o środku O.
Miara kąta CAO jest równa 60^{\circ}
(zobacz rysunek).
Wtedy miara stopniowa kąta ABC jest równa:
Odpowiedzi:
| A. 35^{\circ} | B. 25^{\circ} |
| C. 26^{\circ} | D. 30^{\circ} |
| E. 33^{\circ} | F. 32^{\circ} |
| Zadanie 14. 1 pkt ⋅ Numer: pp-12037 ⋅ Poprawnie: 81/112 [72%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Ciągi (a_n), (b_n),
(c_n) oraz (d_n) są określone dla każdej liczby naturalnej
n > 1 następująco:
a_n=2n^2+3,
b_n=4n+8,
c_n=4^n,
d_n=\frac{9}{n}.
Wskaż zdanie prawdziwe:
Odpowiedzi:
| A. żaden z ciągów nie jest arytmetyczny | B. ciąg a_n jest arytmetyczny |
| C. ciąg d_n jest arytmetyczny | D. ciąg b_n jest arytmetyczny |
| Zadanie 15. 1 pkt ⋅ Numer: pp-12038 ⋅ Poprawnie: 26/36 [72%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
Ciąg (a_n) jest określony wzorem
a_n=(-1)^n\cdot n-5 dla każdej liczby
naturalnej n > 1.
Wtedy trzeci wyraz tego ciągu jest równy:
Odpowiedzi:
| A. 5 | B. -3 |
| C. 12 | D. -18 |
| E. -8 | F. -24 |
| G. 3 | H. -13 |
| Zadanie 16. 1 pkt ⋅ Numer: pp-12039 ⋅ Poprawnie: 12/33 [36%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
W romb o boku 2\sqrt{7} i kącie
60^{\circ} wpisano okrąg.
Promień tego okręgu jest równy:
Odpowiedzi:
| A. \frac{3\sqrt{7}}{4} | B. \sqrt{21} |
| C. \frac{\sqrt{42}}{2} | D. 2\sqrt{21} |
| E. \frac{\sqrt{42}}{4} | F. \frac{\sqrt{21}}{2} |
| Zadanie 17. 1 pkt ⋅ Numer: pp-12040 ⋅ Poprawnie: 6/11 [54%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
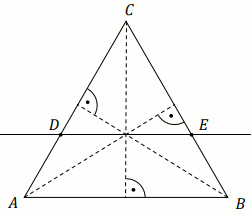
Przez punkt przecięcia wysokości trójkąta równobocznego ABC
poprowadzono prostą DE równoległą do podstawy
AB (zobacz rysunek).
Stosunek pola trójkąta ABC do pola trójkąta CDE jest równy:
Odpowiedzi:
| A. 2:3 | B. 4:9 |
| C. 9:4 | D. 3:2 |
| E. 4:1 | F. 2:1 |
| Zadanie 18. 1 pkt ⋅ Numer: pp-12041 ⋅ Poprawnie: 20/44 [45%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
Końcami odcinka PR są punkty
P=(-3,-4) i R=(1,-2).
Odległość punktu T=(4,1) od środka odcinka PR jest równa:
Odpowiedzi:
| A. \sqrt{23} | B. \sqrt{41} |
| C. \sqrt{73} | D. \sqrt{10} |
| E. \sqrt{21} | F. \sqrt{82} |
| Zadanie 19. 1 pkt ⋅ Numer: pp-12042 ⋅ Poprawnie: 10/11 [90%] | Rozwiąż |
Podpunkt 19.1 (1 pkt)
Kąt \alpha jest ostry oraz
\sin\alpha=\frac{12}{13}.
Wtedy \cos\alpha jest równy:
Odpowiedzi:
| A. \frac{12}{13} | B. \frac{7}{13} |
| C. \frac{8}{13} | D. \frac{2}{13} |
| E. \frac{5}{13} | F. \frac{3}{13} |
| Zadanie 20. 1 pkt ⋅ Numer: pp-12043 ⋅ Poprawnie: 9/11 [81%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
Dane są punkty M=(4,0), N=(4,3)
O=(0,0).
Tangens kąta ostrego MON jest równy:
Odpowiedzi:
| A. \frac{7}{4} | B. \frac{5}{4} |
| C. \frac{3}{4} | D. 1 |
| E. \frac{1}{4} | F. \frac{3}{2} |
| Zadanie 21. 1 pkt ⋅ Numer: pp-12044 ⋅ Poprawnie: 9/11 [81%] | Rozwiąż |
Podpunkt 21.1 (1 pkt)
Proste o równaniach y=-5ax-2 i
y=2x+3a są prostopadłe.
Wtedy a jest równe:
Odpowiedzi:
| A. \frac{3}{20} | B. -\frac{1}{15} |
| C. \frac{1}{5} | D. -\frac{1}{10} |
| E. \frac{1}{10} | F. -\frac{1}{5} |
| Zadanie 22. 1 pkt ⋅ Numer: pp-12045 ⋅ Poprawnie: 10/12 [83%] | Rozwiąż |
Podpunkt 22.1 (1 pkt)
Dany jest trapez ABCD, w którym boki AB i
CD są równoległe oraz C=(-1,7).
Wierzchołki A i B tego trapezu
leżą na prostej o równaniu y=5x+25.
Wtedy bok CD tego trapezu zawiera się w prostej o równaniu:
Odpowiedzi:
| A. y=-\frac{1}{5}x+\frac{34}{5} | B. y=5x+18 |
| C. y=3x+19 | D. y=-\frac{1}{5}x+\frac{21}{5} |
| E. y=5x+12 | F. y=5x+17 |
| Zadanie 23. 1 pkt ⋅ Numer: pp-12046 ⋅ Poprawnie: 4/11 [36%] | Rozwiąż |
Podpunkt 23.1 (1 pkt)
W trapezie równoramiennym ABCD podstawy AB
i CD mają długości równe odpowiednio a
i b (przy czym a > b). Miara
kąta ostrego trapezu jest równa 30^{\circ}.
Wtedy wysokość tego trapezu jest równa:
Odpowiedzi:
| A. \frac{1}{4}\cdot (a-b) | B. \frac{1}{2}\cdot (a-b) |
| C. \frac{\sqrt{3}}{12}\cdot (a+b) | D. \frac{\sqrt{3}}{6}\cdot (a+b) |
| E. \frac{\sqrt{3}}{3}\cdot (a-b) | F. \frac{\sqrt{3}}{6}\cdot (a-b) |
| Zadanie 24. 1 pkt ⋅ Numer: pp-12047 ⋅ Poprawnie: 16/24 [66%] | Rozwiąż |
Podpunkt 24.1 (1 pkt)
Przekątna sześcianu ma długość 3\sqrt{2}.
Wtedy objętość tego sześcianu jest równa:
Odpowiedzi:
| A. 12\sqrt{3} | B. 3\sqrt{6} |
| C. 6 | D. 6\sqrt{6} |
| E. 18\sqrt{2} | F. 6\sqrt{2} |
| Zadanie 25. 1 pkt ⋅ Numer: pp-12051 ⋅ Poprawnie: 13/24 [54%] | Rozwiąż |
Podpunkt 25.1 (1 pkt)
Ostrosłupy prawidłowe trójkątne O_1 i O_2
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa O_1
jest k=2 razy dłuższa od długości krawędzi podstawy
ostrosłupa O_2.
Stosunek objętości ostrosłupa O_1 do objętości ostrosłupa O_2 jest równy:
Odpowiedzi:
| A. 8:1 | B. 1:4 |
| C. 4:1 | D. 1:2 |
| E. 1:8 | F. 2:1 |
| Zadanie 26. 1 pkt ⋅ Numer: pp-12048 ⋅ Poprawnie: 61/94 [64%] | Rozwiąż |
Podpunkt 26.1 (1 pkt)
Wszystkich liczb naturalnych trzycyfrowych parzystych, w których cyfra
1 występuje dokładnie jeden raz, jest:
Odpowiedzi:
| A. 80 | B. 85 |
| C. 105 | D. 90 |
| E. 70 | F. 75 |
| Zadanie 27. 1 pkt ⋅ Numer: pp-12049 ⋅ Poprawnie: 23/36 [63%] | Rozwiąż |
Podpunkt 27.1 (1 pkt)
Ze zbioru liczb naturalnych dwucyfrowych losujemy jedną liczbę.
Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe:
Odpowiedzi:
| A. \frac{1}{5} | B. \frac{4}{15} |
| C. \frac{19}{90} | D. \frac{23}{90} |
| E. \frac{5}{18} | F. \frac{7}{30} |
| Zadanie 28. 1 pkt ⋅ Numer: pp-12050 ⋅ Poprawnie: 47/62 [75%] | Rozwiąż |
Podpunkt 28.1 (1 pkt)
Liczba x jest dodatnia. Mediana zestawu czterech liczb:
1+x, 1+2x,
6+3x, 1, jest równa
13.
Wtedy x jest równe:
Odpowiedzi:
| A. 7 | B. 8.5 |
| C. 7.5 | D. 10.5 |
| E. 8 | F. 10 |
| Zadanie 29. 2 pkt ⋅ Numer: pp-21116 ⋅ Poprawnie: 6/11 [54%] | Rozwiąż |
Podpunkt 29.1 (0.4 pkt)
Rozwiąż nierówność: 3x(x+1) > x^2+x+12.
Rozwiązanie zapisz w postaci sumy przedziałów. Ile jest tych przedziałów?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
Podpunkt 29.2 (0.8 pkt)
Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{min}=
(wpisz liczbę całkowitą)
Podpunkt 29.3 (0.8 pkt)
Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 30. 2 pkt ⋅ Numer: pp-21117 ⋅ Poprawnie: 4/11 [36%] | Rozwiąż |
Podpunkt 30.1 (1 pkt)
Rozwiąż równanie
\frac{3x-1}{3x-1}=3x+1.
Podaj najmniejsze rozwiązanie tego równania.
Odpowiedź:
| x_{min}= | |
Podpunkt 30.2 (1 pkt)
Podaj największe rozwiązanie tego równania.
Odpowiedź:
| x_{min}= | |
| Zadanie 31. 2 pkt ⋅ Numer: pp-21118 ⋅ Poprawnie: 9/44 [20%] | Rozwiąż |
Podpunkt 31.1 (2 pkt)
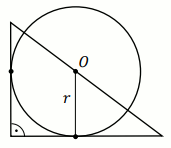
Dany jest trójkąt prostokątny, którego przyprostokątne mają długość
4 i 3. Punkt
O leży na przeciwprostokątnej tego trójkąta i jest
środkiem okręgu stycznego do przyprostokątnych tego trójkąta (zobacz rysunek).
Oblicz długość promienia tego okręgu.
Odpowiedź:
| r= | |
| Zadanie 32. 2 pkt ⋅ Numer: pp-21119 ⋅ Poprawnie: 5/11 [45%] | Rozwiąż |
Podpunkt 32.1 (2 pkt)
Kąt \alpha jest ostry i
\sin\alpha+\cos\alpha=\frac{1}{4}.
Oblicz wartość wyrażenia 2\sin\alpha\cos\alpha.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 33. 2 pkt ⋅ Numer: pp-21120 ⋅ Poprawnie: 15/66 [22%] | Rozwiąż |
Podpunkt 33.1 (2 pkt)
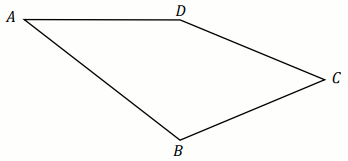
Dany jest czworokąt ABCD, w którym
|BC|=|CD|=|AD|=20 (zobacz rysunek).
Przekątna BD tego czworokąta ma długość
24 i jest prostopadła do boku AD.
Oblicz pole czworokąta ABCD.
Odpowiedź:
| P_{ABCD}= | |
| Zadanie 34. 5 pkt ⋅ Numer: pp-30415 ⋅ Poprawnie: 3/11 [27%] | Rozwiąż |
Podpunkt 34.1 (2 pkt)
Rosnący ciąg arytmetyczny (a_n) jest określony dla każdej
liczby naturalnej n\geqslant 1. Suma pierwszych pięciu
wyrazów tego ciągu jest równa S_5=-20.
Wyrazy a_{5}, a_{7},
a_{15} tworzą – w podanej kolejności – ciąg geometryczny.
Wyznacz trzeci wyraz a_3 tego ciągu.
Odpowiedź:
a_3=
(wpisz liczbę całkowitą)
Podpunkt 34.2 (1 pkt)
Wyznacz różnicę r tego ciągu.
Odpowiedź:
a_3=
(wpisz liczbę całkowitą)
Podpunkt 34.3 (2 pkt)
Zapisz wzór na ogólny wyraz tego ciągu w postaci a_n=an+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |