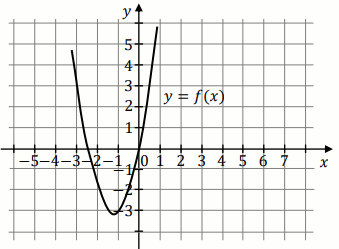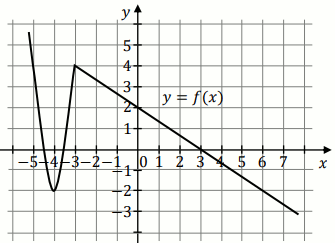⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd arkusza : lo2@cke-2022-06-pp
| Zadanie 1. 1 pkt ⋅ Numer: pp-11878 ⋅ Poprawnie: 424/440 [96%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Liczba \sqrt{45}:\sqrt[3]{216} jest równa:
Odpowiedzi:
| A. \frac{3\sqrt{5}}{8} | B. \frac{\sqrt{5}}{2} |
| C. \frac{3\sqrt{5}}{4} | D. \frac{5\sqrt{5}}{6} |
| E. \frac{\sqrt{5}}{4} | F. \frac{\sqrt{5}}{3} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11879 ⋅ Poprawnie: 471/515 [91%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Liczba \frac{2^{-3}\cdot3^{-1}\cdot4^0}{2^{-1}\cdot3^{-5}\cdot4^{-1}} jest równa:
Odpowiedzi:
| A. \frac{81}{2} | B. \frac{81}{4} |
| C. 2\cdot3^{4} | D. 2\cdot3^{5} |
| E. 4\cdot3^{4} | F. 81 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11880 ⋅ Poprawnie: 327/397 [82%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Liczba dwukrotnie większa od \log{2}+\log{4} jest równa:
Odpowiedzi:
| A. \log{64} | B. \log{4} |
| C. \log{16} | D. 2\log{6} |
| E. \log{32} | F. \log{16} |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11881 ⋅ Poprawnie: 208/234 [88%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
30\% liczby x jest o
2870 mniejsze od liczby x.
Liczba x jest równa:
Odpowiedzi:
| A. 4060 | B. 4280 |
| C. 3970 | D. 4100 |
| E. 4170 | F. 4220 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11882 ⋅ Poprawnie: 339/340 [99%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Dla każdej liczby rzeczywistej a wyrażenie
-6-(6+5a)(6-5a) jest równe
Odpowiedzi:
| A. 25a^2+72 | B. 25a^2-42 |
| C. 5a^2-42 | D. 25a^2+30 |
| E. 5a^2+30 | F. 25a^2-30 |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11883 ⋅ Poprawnie: 126/156 [80%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Jedną z liczb spełniających nierówność x^4-3x^3-15\lessdot 0 jest:
Odpowiedzi:
| A. 4 | B. -5 |
| C. -4 | D. 5 |
| E. -2 | F. 3 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11884 ⋅ Poprawnie: 173/243 [71%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f
określonej wzorem f(x)=2x^2+5x:
Osią symetrii wykresu funkcji g określonej wzorem g(x)=f(x-6) jest prosta o równaniu:
Odpowiedzi:
| A. x=\frac{43}{4} | B. x=-\frac{77}{4} |
| C. x=\frac{67}{4} | D. x=-\frac{53}{4} |
| E. x=\frac{7}{4} | F. x=\frac{19}{4} |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11890 ⋅ Poprawnie: 151/228 [66%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Dana jest funkcja kwadratowa f określona
wzorem f(x)=2x^2-6x. Funkcja kwadratowa
g jest określona wzorem g(x)=2x^2+6x.
Wykres funkcji g jest:
Odpowiedzi:
| A. przesunięty względem wykresu funkcji f o -12 jednostek w kierunku przeciwnym do zwrotu osi Ox | B. symetryczny do wykresu funkcji f względem osi Oy |
| C. symetryczny do wykresu funkcji f względem punktu O=(0,0) | D. symetryczny do wykresu funkcji f względem osi Ox |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11885 ⋅ Poprawnie: 128/150 [85%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Równanie (x^2-4)(x^2+10)=0 ma dokładnie
Odpowiedzi:
| A. cztery rozwiązania | B. jedno rozwiązanie |
| C. trzy rozwiązania | D. dwa rozwiązania |
| Zadanie 10. 1 pkt ⋅ Numer: pp-11886 ⋅ Poprawnie: 221/269 [82%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Funkcja f jest określona wzorem f(x)=\frac{2}{x}-2
dla każdej liczby rzeczywistej x\neq 0.
Liczba f(4)-f(-4) jest równa:
Odpowiedzi:
| A. 0 | B. \frac{3}{4} |
| C. \frac{3}{2} | D. \frac{1}{2} |
| E. 1 | F. -1 |
| Zadanie 11. 1 pkt ⋅ Numer: pp-11887 ⋅ Poprawnie: 162/178 [91%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Punkt M=(3, -2) należy do wykresu funkcji liniowej f
określonej wzorem f(x)=5x+b-15.
Wynika stąd, że b jest równe:
Odpowiedzi:
| A. -3 | B. -8 |
| C. -2 | D. 0 |
| E. -4 | F. 6 |
| Zadanie 12. 1 pkt ⋅ Numer: pp-11889 ⋅ Poprawnie: 204/267 [76%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=-4(x-2)^2+1 jest rosnąca w przedziale:
Odpowiedzi:
| A. \langle -2,+\infty\rangle | B. (-\infty, -2\rangle |
| C. (-\infty, 2\rangle | D. \langle 2,+\infty\rangle |
| Zadanie 13. 1 pkt ⋅ Numer: pp-11888 ⋅ Poprawnie: 160/292 [54%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Na rysunku jest przedstawiony fragment wykresu funkcji okreslonej wzorem
y=f(x):
W przedziale (-4,6) równanie f(x)=-1:
Odpowiedzi:
| A. ma dwa rozwiązania | B. ma trzy rozwiązania |
| C. ma jedno rozwiązanie | D. nie ma rozwiązań |
| Zadanie 14. 1 pkt ⋅ Numer: pp-11904 ⋅ Poprawnie: 211/218 [96%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Ciąg (a_n) jest określony wzorem
a_n=\frac{n-6}{2n^2} dla każdej liczby naturalnej
n \geqslant 1.
Piąty wyraz tego ciągu jest równy:
Odpowiedzi:
| A. -\frac{1}{50} | B. -\frac{1}{6} |
| C. -\frac{1}{75} | D. \frac{1}{98} |
| E. -\frac{1}{16} | F. 0 |
| Zadanie 15. 1 pkt ⋅ Numer: pp-11891 ⋅ Poprawnie: 386/391 [98%] | Rozwiąż |
Podpunkt 15.1 (1 pkt)
Ciąg (a_n), określony dla każdej liczby naturalnej
n \geqslant 1, jest arytmetyczny. Różnica tego ciągu jest równa
2 oraz a_8=3.
Czwarty wyraz tego ciągu jest równy:
Odpowiedzi:
| A. -3 | B. 3 |
| C. -5 | D. -1 |
| E. 1 | F. -7 |
| Zadanie 16. 1 pkt ⋅ Numer: pp-11905 ⋅ Poprawnie: 111/149 [74%] | Rozwiąż |
Podpunkt 16.1 (1 pkt)
Kąt \alpha jest ostry i \sin\alpha=\frac{1}{5}.
Wtedy \cos^2(90^{\circ}-\alpha) jest równy:
Odpowiedzi:
| A. \frac{1}{50} | B. \frac{\sqrt{2}}{50} |
| C. \frac{\sqrt{3}}{50} | D. \frac{1}{25} |
| E. \frac{\sqrt{2}}{25} | F. \frac{2}{25} |
| Zadanie 17. 1 pkt ⋅ Numer: pp-11892 ⋅ Poprawnie: 115/148 [77%] | Rozwiąż |
Podpunkt 17.1 (1 pkt)
Na trójkącie ostrokątnym ABC opisano okrąg o środku O.
Miara kąta ABC jest równa 47^{\circ}.
Miara kąta ACO jest równa:
Odpowiedzi:
| A. 51^{\circ} | B. 41^{\circ} |
| C. 38^{\circ} | D. 39^{\circ} |
| E. 47^{\circ} | F. 43^{\circ} |
| Zadanie 18. 1 pkt ⋅ Numer: pp-11893 ⋅ Poprawnie: 114/196 [58%] | Rozwiąż |
Podpunkt 18.1 (1 pkt)
Trójkąt ABC jest prostokątny. Odcinek AD jest
wysokością tego trójkąta poprowadzoną z wierzchołka A na przeciwprostokątną
BC.
Wtedy:
Odpowiedzi:
| A. \frac{|AD|}{|AB|}=\frac{|AC|}{|AB|} | B. \frac{|AD|}{|AB|}=\frac{|CD|}{|AC|} |
| C. \frac{|AD|}{|AB|}=\frac{|CD|}{|AD|} | D. \frac{|AD|}{|AB|}=\frac{|BC|}{|BD|} |
| Zadanie 19. 1 pkt ⋅ Numer: pp-11894 ⋅ Poprawnie: 137/189 [72%] | Rozwiąż |
Podpunkt 19.1 (1 pkt)
Pole rombu o obwodzie 8 i kącie rozwartym
120^{\circ} jest równe:
Odpowiedzi:
| A. 4\sqrt{3} | B. \frac{4\sqrt{3}}{3} |
| C. 2\sqrt{3} | D. 2 |
| E. \sqrt{3} | F. 6 |
| Zadanie 20. 1 pkt ⋅ Numer: pp-11895 ⋅ Poprawnie: 122/148 [82%] | Rozwiąż |
Podpunkt 20.1 (1 pkt)
W trójkącie miary kątów są równe: \alpha+2^{\circ},
4\alpha+8^{\circ}, \alpha+32^{\circ}.
Miara największego kąta tego trójkąta jest równa:
Odpowiedzi:
| A. 98^{\circ} | B. 97^{\circ} |
| C. 95^{\circ} | D. 99^{\circ} |
| E. 100^{\circ} | F. 96^{\circ} |
| Zadanie 21. 1 pkt ⋅ Numer: pp-11896 ⋅ Poprawnie: 222/214 [103%] | Rozwiąż |
Podpunkt 21.1 (1 pkt)
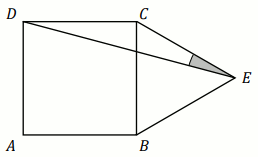
Na boku BC kwadratu ABCD (na zewnątrz) zbudowano
trójkąt równoboczny BEC (zobacz rysunek).
Miara kąta DEC jest równa:
Odpowiedzi:
| A. 20^{\circ} | B. 18^{\circ} |
| C. 12^{\circ} | D. 10^{\circ} |
| E. 15^{\circ} | F. 24^{\circ} |
| Zadanie 22. 1 pkt ⋅ Numer: pp-11897 ⋅ Poprawnie: 118/173 [68%] | Rozwiąż |
Podpunkt 22.1 (1 pkt)
Proste o równaniach y=-\frac{2}{3}x-2 oraz y=\frac{6}{2m+2}x+1
są prostopadłe.
Wynika z tego, że:
Odpowiedzi:
| A. m=\frac{2}{3} | B. m=\frac{1}{3} |
| C. m=\frac{1}{2} | D. m=\frac{3}{2} |
| E. m=1 | F. m=2 |
| Zadanie 23. 1 pkt ⋅ Numer: pp-11898 ⋅ Poprawnie: 115/177 [64%] | Rozwiąż |
Podpunkt 23.1 (1 pkt)
Proste o równaniach y=-3x+\frac{34}{3} oraz
y=\frac{1}{3}x-2 przecinają się w punkcie
P=(x_0,y_0).
Wynika z tego, że:
Odpowiedzi:
| A. x\lessdot 0\ \wedge\ y>0 | B. x>0\ \wedge\ y>0 |
| C. x>0\ \wedge\ y\lessdot 0 | D. x\lessdot 0\ \wedge\ y\lessdot 0 |
| Zadanie 24. 1 pkt ⋅ Numer: pp-11900 ⋅ Poprawnie: 185/214 [86%] | Rozwiąż |
Podpunkt 24.1 (1 pkt)
Liczba wszystkich krawędzi graniastosłupa jest równa 57.
Liczba wszystkich wierzchołków tego graniastosłupa jest równa:
Odpowiedzi:
| A. 43 | B. 42 |
| C. 41 | D. 35 |
| E. 38 | F. 33 |
| Zadanie 25. 1 pkt ⋅ Numer: pp-11901 ⋅ Poprawnie: 185/216 [85%] | Rozwiąż |
Podpunkt 25.1 (1 pkt)
W ostrosłupie prawidłowym trójkątnym wszystkie krawędzie mają długość 16.
Pole powierzchni całkowitej tego ostrosłupa jest równe:
Odpowiedzi:
| A. 256\sqrt{3} | B. 768 |
| C. 512\sqrt{3} | D. 256 |
| E. 384 | F. 128\sqrt{3} |
| Zadanie 26. 1 pkt ⋅ Numer: pp-11902 ⋅ Poprawnie: 295/386 [76%] | Rozwiąż |
Podpunkt 26.1 (1 pkt)
Rozważamy wszystkie liczby naturalne k=6-cyfrowe, których suma
cyfr jest równa 3 i ich zapis zawiera dokładnie trzy różne cyfry.
Wszystkich takich liczb jest:
Odpowiedzi:
| A. 16 | B. 14 |
| C. 11 | D. 10 |
| E. 12 | F. 13 |
| Zadanie 27. 1 pkt ⋅ Numer: pp-11903 ⋅ Poprawnie: 313/353 [88%] | Rozwiąż |
Podpunkt 27.1 (1 pkt)
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest 2 razy
więcej niż czarnych, a czarnych jest 4 razy więcej niż zielonych.
Z pudełka losujemy jedną kulę.
Prawdopodobieństwo wylosowania kuli białej jest równe:
Odpowiedzi:
| A. \frac{24}{65} | B. \frac{8}{39} |
| C. \frac{8}{13} | D. \frac{48}{65} |
| E. \frac{16}{39} | F. \frac{6}{13} |
| Zadanie 28. 1 pkt ⋅ Numer: pp-11906 ⋅ Poprawnie: 250/264 [94%] | Rozwiąż |
Podpunkt 28.1 (1 pkt)
W pewnej grupie uczniów przeprowadzono ankietę na temat liczby odsłuchanych audiobooków
w lutym 2022 roku. Wyniki ankiety przedstawiono w tabeli:
Liczba audiobooków: 1| 3| 4| 6| 8| 10| -------------------------------------------- Liczba uczniów : 1| 10| 6| 5| 9| 1|
Mediana liczby odsłuchanych audiobooków w tej grupie uczniów jest równa:
Odpowiedzi:
| A. 3 | B. 4 |
| C. 8 | D. 10 |
| E. 6 | F. 1 |
| Zadanie 29. 2 pkt ⋅ Numer: pp-21072 ⋅ Poprawnie: 114/148 [77%] | Rozwiąż |
Podpunkt 29.1 (1 pkt)
Rozwiąż nierówność
-3x^2+4\geqslant 4x.
Rozwiązanie zapisz w postaci przedziału lub sumy przedziałów. Podaj ten z końców liczbowych, który jest liczbą całkowitą.
Odpowiedź:
x_{\in\mathbb{Z}}=
(wpisz liczbę całkowitą)
Podpunkt 29.2 (1 pkt)
Podaj ten z końców liczbowych, który nie jest liczbą całkowitą.
Odpowiedź:
| x_{\notin\mathbb{Z}}= | |
| Zadanie 30. 2 pkt ⋅ Numer: pp-21073 ⋅ Poprawnie: 75/162 [46%] | Rozwiąż |
Podpunkt 30.1 (1 pkt)
Funkcja kwadratowa f określona wzorem f(x)=ax^2+bx+c ma dokładnie jedno miejsce
zerowe równe -4. Ponadto f(0)=64.
Wyznacz współczynnik a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 30.2 (1 pkt)
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 31. 2 pkt ⋅ Numer: pp-21074 ⋅ Poprawnie: 141/217 [64%] | Rozwiąż |
Podpunkt 31.1 (2 pkt)
Trójwyrazowy ciąg (x-6,3x-16,9x-38) jest geometryczny.
Oblicz x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
| Zadanie 32. 2 pkt ⋅ Numer: pp-21076 ⋅ Poprawnie: 75/196 [38%] | Rozwiąż |
Podpunkt 32.1 (2 pkt)
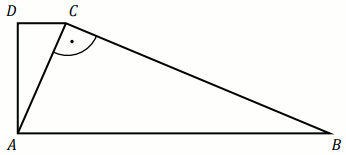
Dany jest trapez prostokątny ABCD. Podstawa AB
tego trapezu jest równa 17, a ramię BC
ma długość 15. Przekątna AC tego trapezu jest
prostopadła do ramienia BC (zobacz rysunek).
Oblicz długość ramienia AD.
Odpowiedź:
| |AD|= | |
| Zadanie 33. 2 pkt ⋅ Numer: pp-21077 ⋅ Poprawnie: 180/310 [58%] | Rozwiąż |
Podpunkt 33.1 (2 pkt)
Ze zbioru wszystkich liczb naturalnych dwucyfrowych większych od 31
losujemy jedną liczbę. Niech A oznacza zdarzenie polegające na wylosowaniu
liczby podzielnej przez 7.
Oblicz prawdopodobieństwo zdarzenia A.
Odpowiedź:
| P(A)= | |
| Zadanie 34. 5 pkt ⋅ Numer: pp-30408 ⋅ Poprawnie: 33/177 [18%] | Rozwiąż |
Podpunkt 34.1 (2 pkt)
Punkt A=(4,-2) jest wierzchołkiem trójkąta
ABC, w którym |AC|=|BC|.
Punkt S=\left(8,\frac{1}{4}\right) jest środkiem odcinka
AB. Wierzchołek C tego trójkąta należy
do prostej o równaniu y=x+8.
Oblicz współrzędne wierzchołka B=(x_B, y_B) tego trójkąta.
Odpowiedzi:
| x_B | = | (dwie liczby całkowite) | |
| y_B | = | (dwie liczby całkowite) | |
Podpunkt 34.2 (3 pkt)
Oblicz współrzędne wierzchołka C=(x_C, y_C) tego trójkąta.
Odpowiedzi:
| x_C | = | (dwie liczby całkowite) | |
| y_C | = | (dwie liczby całkowite) | |