Podgląd arkusza : lo2@cke-2022-08-pp

 Liczba \frac{25^{-48}}{5^{10}} jest równa:

 Liczba \log_{3}{243}-\log_{3}{9} jest równa:

 Liczba \left(3+3\sqrt{2}\right)^2 jest równa:

 Cenę x (w złotych) pewnego towaru obniżono najpierw o 30\%, a następnie obniżono o 40\% w odniesieniu do ceny obowiązującej w danym momencie.

Po obydwu tych obniżkach cena towaru jest równa:

 Jednym z rozwiązań równania 7(x+4)-x^2(x+4)=0 jest liczba:

 Zbiorem wszystkich rozwiązań nierówności \frac{5x-3}{8}>-5x jest przedział:

 Suma wszystkich rozwiązań równania (3x+3)(3x-4)(x+2)=0 jest równa:

 Punkt A=(1,2) należy do wykresu funkcji f, określonej wzorem f(x)=(m^2+2m-2)x^3-m^2-m+1 dla każdej liczby rzeczywistej x.

Wtedy liczba m jest równa:

 Funkcja liniowa f określona wzorem f(x)=(4m+4)x+22 jest rosnąca dla:

 Funkcja kwadratowa f określona wzorem f(x)=x^2+bx+c osiąga dla x=-2 wartość najmniejszą równą 6.

Wtedy:

 Dana jest funkcja kwadratowa f określona wzorem f(x)=-4(x-4)(x+5).

Funkcja f jest rosnąca w zbiorze:

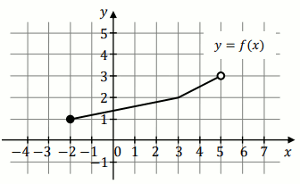
 Na rysunku przedstawiono wykres funkcji f określonej na zbiorze \langle -2, 5):

Funkcja g jest określona za pomocą funkcji f następująco: g(x)=f(x-1). Wykres funkcji g można otrzymać poprzez odpowiednie przesunięcie wykresu funkcji f.

Dziedziną funkcji g jest zbiór:

 Dane są ciągi a_n=3n oraz b_n=4n-2, określone dla każdej liczby naturalnej n\geqslant 1.

Liczba 39:

 Dany jest ciąg geometryczny (a_n), określony dla każdej liczby naturalnej n\geqslant 1. Drugi wyraz tego ciągu oraz iloraz ciągu (a_n) są równe 3.

Suma sześciu początkowych kolejnych wyrazów tego ciągu jest równa:

 W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 2640 guzików.

Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.

 Przyprostokątna AC trójkąta prostokątnego ABC ma długość 6, a przeciwprostokątna AB ma długość \sqrt{61}.

Wtedy tangens kąta ostrego CAB tego trójkąta jest równy:

 Nie istnieje kąt ostry \alpha taki, że:

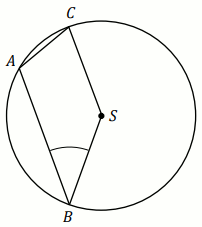
 Wierzchołki A, B, C czworokąta ABSC leżą na okręgu o środku S. Kąt ABS ma miarę 54^{\circ} (zobacz rysunek), a przekątna BC jest dwusieczną tego kąta.

Miara kąta ASC jest równa:

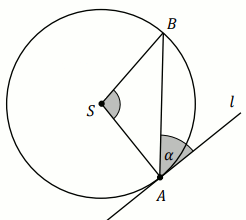
 Punkty A oraz B leżą na okręgu o środku S. Kąt środkowy ASB ma miarę 124^{\circ}. Prosta l jest styczna do tego okręgu w punkcie A i tworzy z cięciwą AB okręgu kąt o mierze \alpha (zobacz rysunek).

Wtedy:

 Pole prostokąta jest równe 588, a przekątne tego prostokąta przecinają się pod kątem ostrym \alpha, takim, że \sin\alpha=\frac{1}{6}.

Długość przekątnej tego prostokąta jest równa:

 Proste o równaniach y=\frac{3}{5}x-4 oraz y=(2m-5)x+4 są prostopadłe, gdy:

 Punkty A=(1,4) oraz C=(-5,3) są końcami przekątnej AC rombu ABCD.

Środek przekątnej BD tego rombu ma współrzędne:

 Punkty A=(-11,11), B=(0,13), C=(5,3) są wierzchołkami równoległoboku ABCD.

Długość przekątnej BD tego równoległoboku jest równa:

 Obrazem prostej o równaniu y=-5x+3 w symetrii osiowej względem osi Ox jest prosta o równaniu:

 W graniastosłupie prawidłowym stosunek liczby wszystkich krawędzi do liczby wszystkich ścian jest równy \frac{8}{3}.

Podstawą tego graniastosłupa jest n-kąt foremny. Liczba n jest równa:

 Średnia arytmetyczna zestawu liczb a, b c, d jest równa 70.

Wtedy średnia arytmetyczna zestawu liczb a-13, b+17,c,d jest równa:

 Wszystkich trzycyfrowych liczb naturalnych większych od 400 o wszystkich cyfrach parzystych jest:

 Doświadczenie losowe polega na dwukrotnym rzucie symetryczną, 18-śnienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego do 18. Niech p oznacza prawdopodobieństwo otrzymania w drugim rzucie liczby oczek podzielnej przez 9.

Wtedy:

 Rozwiąż nierówność 5x^2+34x\geqslant -24.

Rozwiązanie zapisz w postaci sumy przedziałów. Ile jest tych przedziałów?

 Podaj ten z końców liczbowych tych przedziałów, który jest liczbą całkowitą.

 Podaj ten z końców liczbowych tych przedziałów, który nie jest liczbą całkowitą.

 Trójwyrazowy ciąg (x+1,y,y+4) jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.

Wyznacz x.

 Wyznacz y.

 Rozwiąż równanie \frac{4}{x+4}=x+1

Podaj najmniejsze rozwiązanie tego równania.

 Podaj największe rozwiązanie wymierne tego równania.

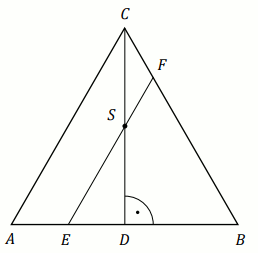
 Dany jest trójkąt równoboczny ABC o boku długości 26. Punkt E leży na boku AB, a punkt F – na boku BC tego trójkąta. Odcinek EF jest równoległy do boku AC i przechodzi przez środek S wysokości CD trójkąta ABC (zobacz rysunek).

Oblicz długość odcinka EF.

 Ze zbioru pięciu liczb \{-5,-4,4,8,10\} losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie A polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny.

Oblicz prawdopodobieństwo zdarzenia A.

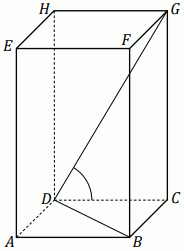
 Dany jest graniastosłup prosty ABCDEFGH, którego podstawą jest prostokąt ABCD. W tym graniastosłupie |BD|=52, a ponadto |CD|=28+|BC| oraz |\sphericalangle CDG|=45^{\circ} (zobacz rysunek).

Oblicz pole podstawy tego graniastosłupa.

 Oblicz objętość tego graniastosłupa.

 Oblicz pole powierzchni bocznej tego graniastosłupa.