Podgląd testu : lo2@sp-04-funkcje-pp-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10695 ⋅ Poprawnie: 368/949 [38%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Funkcja f każdej liczbie rzeczywistej
przypisuje połowę sześcianu tej liczby, pomniejszoną o 8.
Funkcję f opisuje wzór:
Odpowiedzi:
| T/N : f(x)=\frac{x^3-8}{2} | T/N : f(x)=\frac{1}{2}x^6-8 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10734 ⋅ Poprawnie: 677/971 [69%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Do wykresu funkcji
f(x)=\frac{a}{x+4} należy punkt
A=\left(-3,7\right).
Wyznacz wartość parametru a.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10735 ⋅ Poprawnie: 277/402 [68%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Do wykresu funkcji określonej wzorem
f(x)=(m+3)x-1 należy punkt
S=(4,23).
Wyznacz wartość parametru m.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10694 ⋅ Poprawnie: 487/767 [63%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Zbiór liczb rzeczywistych jest dziedziną funkcji:
Odpowiedzi:
| T/N : f(x)=\frac{x-1}{x^2} | T/N : f(x)=\frac{1}{x+3} |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10686 ⋅ Poprawnie: 326/516 [63%] | Rozwiąż |
Podpunkt 5.1 (0.8 pkt)
Dziedziną funkcji g(x)=\sqrt{6-\frac{6x-9}{2}}
jest pewien przedział.
Podaj ten koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 5.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. 4 | B. 0 |
| C. +\infty | D. 3 |
| E. -\infty | F. 7 |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10707 ⋅ Poprawnie: 558/763 [73%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Liczby f_{min} i f_{max} sa odpowiednio
najmniejszą i największą wartością funkcji, której wykres pokazano na rysunku:
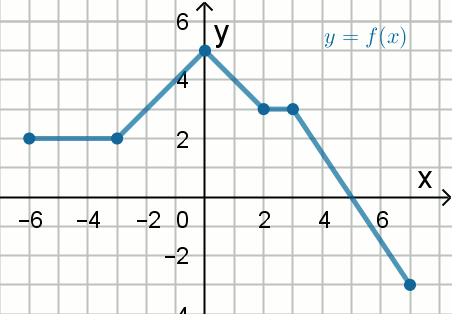

Podaj liczby f_{min} i f_{max}.
Odpowiedzi:
| f_{min} | = |
(wpisz liczbę całkowitą) |
| f_{max} | = |
(wpisz liczbę całkowitą) |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10745 ⋅ Poprawnie: 165/248 [66%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Funkcja f przyporządkowuje każdej liczbie naturalnej
większej od 1 jej największy dzielnik będący liczbą
pierwszą.
Spośród liczb: f(51), f(52), f(54), f(55) największa to:
Odpowiedzi:
| A. f(52) | B. f(51) |
| C. f(54) | D. f(55) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10728 ⋅ Poprawnie: 472/597 [79%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
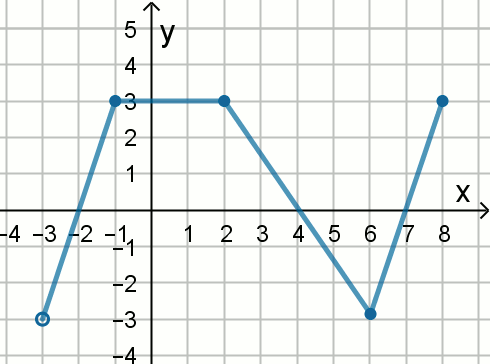

Podaj największą wartość tej funkcji.
Odpowiedź:
f_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 9. 1 pkt ⋅ Numer: pp-10753 ⋅ Poprawnie: 58/83 [69%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Wartością funkcji dla argumentu naturalnego n jest
ostatnia cyfra kwadratu liczby n zwiększona o
2. Wynika stąd, że zbiór wartości funkcji zawiera
liczbę:
Odpowiedzi:
| A. 7 | B. 9 |
| C. 4 | D. 5 |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10760 ⋅ Poprawnie: 61/114 [53%] | Rozwiąż |
Podpunkt 10.1 (0.5 pkt)
Zbiorem wartości funkcji f jest przedział
\langle -16,5\rangle.
Wyznacz zbiór tych wartości parametru q, dla których
funkcja określona wzorem g(x)=f(x)+q nie ma miejsc zerowych.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych tych przedziałów.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (0.5 pkt)
Podaj największy z końców liczbowych tych przedziałów.
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 11. 1 pkt ⋅ Numer: pp-11690 ⋅ Poprawnie: 55/91 [60%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Wyznacz najmniejszą wartość funkcji określonej wzorem f(x)=\frac{4}{3}x+\frac{4}{5}
w przedziale \langle -3,1\rangle.
Odpowiedź:
| f_{min}(x)= | |
| Zadanie 12. 1 pkt ⋅ Numer: pp-10741 ⋅ Poprawnie: 604/941 [64%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
Liczby -8 i 8 są miejscami
zerowymi funkcji:
Odpowiedzi:
| A. f(x)=\frac{1}{128}x^2-\frac{1}{2} | B. f(x)=\frac{(x-8)(x+8)}{x^2-64} |
| C. f(x)=x^2-16x+64 | D. f(x)=x(x+8) |
| Zadanie 13. 1 pkt ⋅ Numer: pp-10726 ⋅ Poprawnie: 326/865 [37%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
Rysunek przedstawia wykres funkcji f:
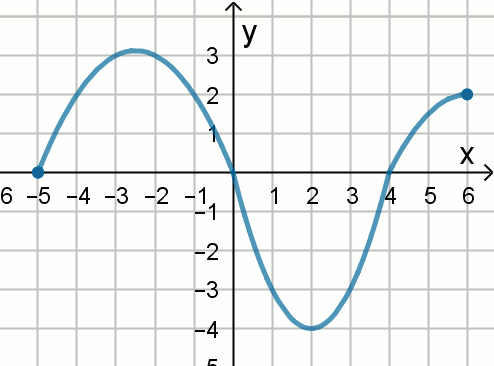

Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : funkcja ta ma dwa miejsca zerowe | T/N : zbiór wartości funkcji jest zawarty w \langle -4,4) |
| Zadanie 14. 1 pkt ⋅ Numer: pp-10700 ⋅ Poprawnie: 508/905 [56%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji h:
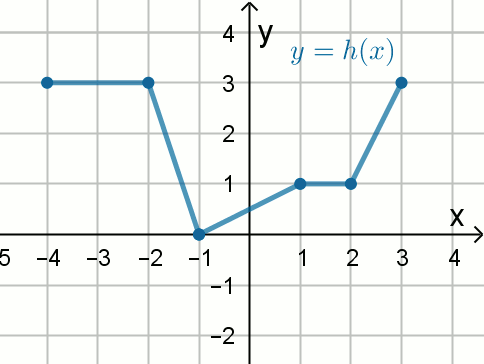

Jaką długość ma najdłuższy przedział, w którym funkcja h jest monotoniczna?
Odpowiedź:
d=
(wpisz liczbę całkowitą)