Podgląd testu : lo2@sp-04-funkcje-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10757 ⋅ Poprawnie: 490/769 [63%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Do wykresu funkcji f należy punkt o współrzędnych
(-8,4) oraz
f(8)=0.
Funkcja f opisana jest wzorem:
Odpowiedzi:
| A. f(x)=\frac{8}{x} | B. f(x)=4x-3 |
| C. f(x)=3x^2 | D. f(x)=\sqrt{-x+8} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10731 ⋅ Poprawnie: 403/922 [43%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji
y=f(x).
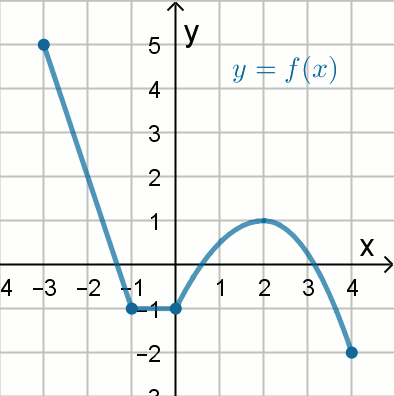

W którym z przedziałów, funkcja przyjmuje wartość 1:
Odpowiedzi:
| A. (-3,-2) | B. (-1,2) |
| C. \langle 2,4) | D. (2,3) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10690 ⋅ Poprawnie: 106/209 [50%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Wyznacz dziedzinę funkcji określonej wzorem
f(x)=\sqrt{x+3}\sqrt{x-11}
i zapisz rozwiązanie w postaci sumy przedziałów.
Liczba x_0 jest największym z końców liczbowych tych przedziałów.
Liczba m jest najmniejszą liczbą całkowitą z dziedziny tej funkcji.
Liczba x_0 jest największym z końców liczbowych tych przedziałów.
Liczba m jest najmniejszą liczbą całkowitą z dziedziny tej funkcji.
Podaj liczby x_0 i m.
Odpowiedzi:
| x_0 | = |
(wpisz liczbę całkowitą) |
| m | = |
(wpisz liczbę całkowitą) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10687 ⋅ Poprawnie: 305/500 [61%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wyznacz dziedzinę D_f funkcji określonej wzorem
f(x)=\sqrt{5-x}-\sqrt{17-x}
.
Podaj największą liczbę całkowitą, która należy do zbioru D_f.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10721 ⋅ Poprawnie: 219/402 [54%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Wykres funkcji f pokazano na rysunku:
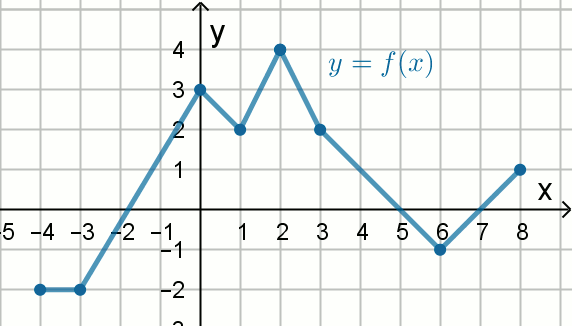
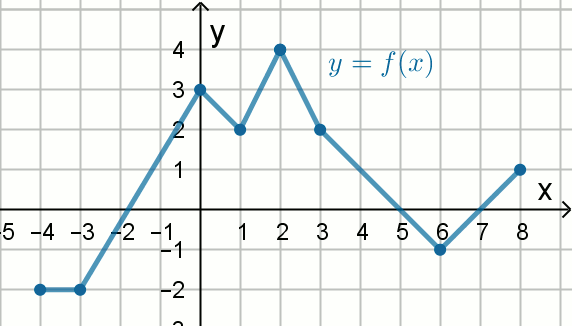
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : f(2) > \left[f(3)\right]^2 | T/N : \left[f(-2)\right]^2 < f(4) |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10717 ⋅ Poprawnie: 187/246 [76%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Funkcja f przyporządkowuje każdej liczbie
naturalnej resztę z dzielenia tej liczby przez 8.
Oblicz wartość wyrażenia \frac{f(27)}{f(37)}.
Odpowiedź:
| \frac{f(m)}{f(n)}= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10710 ⋅ Poprawnie: 93/138 [67%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Funkcja f określona jest wzorem
f(x)=\sqrt[3]{x}-\frac{1}{\sqrt[3]{x^2}}.
Wtedy liczba f(-4) jest równa:
Odpowiedzi:
| A. -\frac{4}{5}\sqrt[3]{16} | B. -\frac{4}{5}\sqrt[3]{4} |
| C. -\frac{5}{4}\sqrt[3]{4} | D. -\frac{5}{4}\sqrt[3]{16} |
| Zadanie 8. 1 pkt ⋅ Numer: pr-10089 ⋅ Poprawnie: 6/6 [100%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
» Dana jest funkcja f określona wzorem
f(x)=\left\lbrace
\begin{array}{ll}
(x+3)^3 & \text{dla } -4\leqslant x \lessdot -1\\
-x^2-6x-5 & \text{dla } -1\leqslant x \leqslant 3
\end{array}
.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : f(0)-f(-5) \lessdot 0 | T/N : f(-4)+f(-3) > 0 |
| Zadanie 9. 1 pkt ⋅ Numer: pp-11691 ⋅ Poprawnie: 37/56 [66%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Wyznacz najmniejszą wartość funkcji określonej wzorem f(x)=-\frac{1}{6}x^2-4,
w przedziale \langle -6,-5\rangle.
Odpowiedź:
| f_{min}(x)= | |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10706 ⋅ Poprawnie: 751/959 [78%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Liczba 1 jest miejscem zerowym
funkcji f(x)=(2m-1)x+3.
Wyznacz wartość parametru m.
Odpowiedź:
m=
(wpisz liczbę całkowitą)
| Zadanie 11. 1 pkt ⋅ Numer: pr-10093 ⋅ Poprawnie: 2/3 [66%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
» Funkcja f opisana jest wzorem
f(x)=\left\lbrace
\begin{array}{ll}
x^3 & \text{dla }x \in(-1,0\rangle\\
x^5-33 & \text{dla }x > 2\\
3x^3-x^2 & \text{dla }x\in(0,2)
\end{array}
i ma k miejsc zerowych.
Wyznacz liczbę k.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 12. 1 pkt ⋅ Numer: pr-10091 ⋅ Poprawnie: 2/3 [66%] | Rozwiąż |
Podpunkt 12.1 (1 pkt)
» Wyznacz największe miejsce zerowe funkcji określonej wzorem
f(x)=\left\lbrace
\begin{array}{ll}
x & \text{dla }x \geqslant 2\\
x^2-4 & \text{dla }x \lessdot 2
\end{array}
.
Odpowiedź:
x_{max}=
(wpisz liczbę całkowitą)
| Zadanie 13. 1 pkt ⋅ Numer: pp-10698 ⋅ Poprawnie: 205/563 [36%] | Rozwiąż |
Podpunkt 13.1 (1 pkt)
«« Dziedziną funkcji f jest przedział
\langle -5,4\rangle:
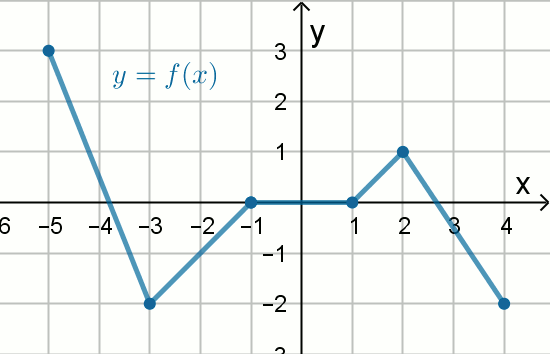
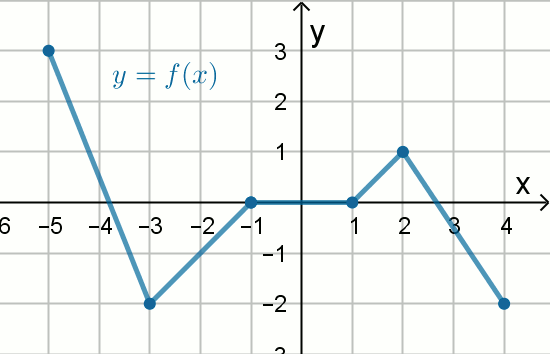
Jaką długość ma najdłuższy przedział, w którym funkcja f jest malejąca?
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 14. 1 pkt ⋅ Numer: pr-10281 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 14.1 (1 pkt)
» Które z poniższych wzorów opisują funkcję nieparzystą?
Odpowiedzi:
| T/N : f(x)=x^8+x^4-x^2 | T/N : f(x)=-3x |
| T/N : f(x)=\frac{x^2-4}{|x-2|} |